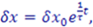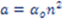dove
e’ chiamato l’esponente di Lyapunov. Notare che per tempi
l’amplificazione di fluttuazioni microscopiche e’ cosi’ spinta che la prevedibilita’ di qualsiasi traiettoria individuale e’ completamente impossibile.
Ma cosa possiamo dire riguardo al nostro sistema solare? Si tratta di un sistema dinamico stabile? E’ possibile per esempio, predire il moto di un singolo pianeta per i prossimi miliardi di anni?
Essendo il sistema solare, un sistema con molti gradi di liberta’ (9 pianeti piu’ il sole che moltiplicato per i 3 gradi di liberta’ di ognuno fanno 30 gradi di liberta’) e’ chiaro che ci si aspetta un sistema dinamico caotico. E questo in effetti e’ il risultato ottenuto di recente dal team del ricercatore Laskar, che con delle simulazioni numeriche molto accurate, e’ riuscito a stimare un tempo di Lyupanov per l’intero sistema solare di circa 5 milioni di anni. Questo significa che un’incertezza iniziale di 1 Km sulla posizione iniziale di un pianeta, puo’ arrivare ad un’unita astronomica (AU=1.5E+8 Km) dopo 95 milioni di anni.
Il fatto che l’esponente di Lyapunov non e’ molto grande, significa che il sistema solare non ha un alto grado di caoticita’, dovuto alla possibilita’ di trascurare l’interazione gravitazionale tra i pianeti rispetto a quella tra i pianeti e il sole. Come esempio di esponente di Lyapunov, nella figura 1, viene riportata la divergenza tra due orbite di Plutone inizialmente molto vicine al trascorrere degli anni.
Figura 1: La divergenza d (in unita’ astronomiche) tra due orbite di Plutone inizialmente vicine, cresce esponenzialmente nel tempo (in milioni di anni). Il fit lineare dei dati, comporta un tempo di Lyupanov dell’ordine dei 10 milioni di anni.
Gli studi al computer della storia caotica del sistema solare, sono diventati un ramo molto importante ed interessante della fisica non-lineare, che hanno aperto nuove possibilita’ per la comprensione delle orbite dei pianeti del sistema solare e di altre stelle. In effetti, ci sono state speculazioni sulla struttura numerica delle orbite dei pianeti, fin dal diciottesimo secolo, quando J. Titius e J. Bode notarono una relazione regolare tra le distanze medie dei pianeti dal sole come indicato nella Tabella 1. Ponendo la distanza Terra-Sole uguale ad un’unita’ astonomica (AU), la regola di Titius-Bode e’ data da:
dove a e’ la distanza media del pianeta dal sole in AU ed n e’ il numero planetario che corrisponde a 0 per Venere e per Mercurio. Questa formula riusci’ a predire con buona approssimazione la posizione di Urano, scoperto nel 1781, cioe’ 9 anni dopo la formulazione della regola. Tuttavia per Nettuno e Plutone scoperti successivamente, la formula di Titius-Bode si e’ dimostrata essere non precisa e questo ha fatto si che diversi studiosi, hanno elaborato una versione piu’ recente capace di predire non solo le distanze di Nettuno e Plutone ma anche dei satelliti di Giove, Saturno ed Urano. L’accordo tra le distanze predette e quelle osservate per i vari satelliti e’ qualche cosa di eccezionale con degli errori di alcuni per cento. La versione recente della legge di Titius-Bode e’ data da:
con k una costante uguale a 0.21363 AU e
Ultimamente, sempre il ricercatore Laskar e il suo team, usando una combinazione di tecniche numeriche ed analitiche, ha scoperto la seguente relazione, valida non solo per il sistema solare ma anche per i pianeti extrasolari recentemente scoperti:
dove a, come sempre e’ la distanza media dal sole, n il numero planetario e k una costante. Laskar ha trovato k=0.14 per i pianeti interni del sistema solare e 0.81 per i pianeti esterni.
Tabella 1: Distanze medie planetarie dal sole in unita’ astonomiche e corrispondenti valori della regola di Titius-Bode, dei risultati di Laskar e del modello quantistico di Nottale.
Sia la legge di Titius-Bode che i calcoli numerici di Laskar, suggeriscono un qualche ordine sottostante, una qualche regolarita’ celeste paragonabile a quella dell’atomo di idrogeno prima della versione quantizzata di Bohr e Schroedinger. Proprio da questo tipo di osservazioni e’ partita l’analisi del gruppo di uno studioso francese, Laurent Nottale, che ha congetturato che le traiettorie degli elettroni negli atomi e i pianeti del sistema solare su una scala temporale maggiore di 0.1 miliardi di anni subiscono una sorta di moto Browniano, che e’ continuo ma non differenziabile, come il perimetro di una curva di Koch o di una costa marina. Essi hanno proposto una teoria per calcolare le probabilita’ delle orbite planetarie che da un punto di vista formale sono identiche a quelle della meccanica quantistica formulate da Schroedinger e Bohr per le orbite elettroniche negli atomi, nonostante l’utilizzo di parametri completamente diversi. Come per il caso dei raggi delle orbite elettroniche dell’atomo di idrogeno, proporzionali al quadrato di n, Laurent Nottale e il suo gruppo ritiene che le distanze medie dei pianeti siano date da:
dove n e’ l’indice orbitale e alfa una costante di proporzionalita’ per i pianeti interni (indicata col pedice i) ed esterni (indicata col pedice o).
Poiche’ per i pianeti interni risulta
e l’indice di Mercurio e’ uguale a 3, questo significa che c’e’ la possibilita’ di due pianeti interni molto vicini al Sole, molto probabilmente evaporati dal calore del Sole o uno evaporato (quello piu’ vicino al Sole) e l’altro ancora da scoprire. La costante dei pianeti esterni, invece, e’ pari a 1.125 AU. La relazione di Nottale e’ in ottimo accordo con i dati misurati, compresi gli asteroidi piu’ grandi, i satelliti dei pianeti del sistema solare e anche di molti dei pianeti extrasolari (vedi figura 2).
Ma questi risultati sono delle idee credibili da un punto di vista scientifico o si tratta di semplice numerologia? Al momento e’ difficile dirlo. Solo le osservazioni di altri pianeti extrasolari ed extragalattici, ed ulteriori studi teorici in quest’area potranno fornire, una risposta definitiva. Al momento lasciamoci sorprendere dalla grande efficacia della matematica nel descrivere tutto cio’ che ci circonda dall’infinitamente piccolo all’infinitamente grande.
Figura 2: Radice quadrata del rapporto (a/M) con a in AU ed M in masse solari in funzione dell’intero n, per i pianeti interni del sistema solare e alcuni pianeti extrasolari scoperti da poco.
Appunti di viaggio di un fisico curioso...... della bellezza di tutto quello che ci circonda,dell'irragionevole efficacia della matematica nello spiegare il mondo intorno a noi, della continua lotta della vita tra ordine e caos, curioso dell'emergenza della complessita' da regole elementari e tant'altro....... Sara' un viaggio divertente e spero ricco di sorprese.
domenica 11 novembre 2012
L’armonia planetaria
martedì 23 ottobre 2012
0.0001 Il numero della solitudine cosmica
Un matematico dell’Università’ di East Anglia, A. Watson, ha rivolto il suo sguardo alle stelle cercando di dare una risposta ad una delle questioni più antiche dell’umanità’: siamo soli nell’Universo? La risposta con molta probabilità e’ si. L’Astrobiologia e’ un nuovo campo della scienza che si occupa dello studio dell’origine, distribuzione, evoluzione e destino della vita ovunque essa si trovi nell’Universo incluso la Terra. A questo proposito il prof. A. Watson ha sviluppato un modello matematico per esaminare la possibilità di presenza di vita intelligente in pianeti simili alla Terra considerando quanto tempo ancora rimane alla terra prima che il Sole diventi troppo brillante per la sopravvivenza della vita. Nell’articolo “Implications of an anthropic model of evolution for emergence of complex life and intelligence” pubblicato qualche anno fa, A. Watson ha postulato che per degli osservatori intelligenti prima di evolversi c’e’ bisogno di passare attraverso un numero n di fasi molto difficili da un punto di vista evolutivo. Una volta superati questi “gradini”, l’evoluzione procede velocemente fino a che non viene raggiunto il successivo stadio. La vita intelligente si e’ evoluta molto tardi sulla Terra e A. Watson suggerisce che questo può essere legato alla difficolta’ nel superare i primi n stadi più difficili. Egli suggerisce che n e’ meno di 10 e molto probabilmente uguale a 4. Questi stadi includono l’emergenza di batteri unicellulari, batteri complessi pluricellulari, cellule che permettono forme di vita complessa e vita intelligente. Il professore A. Watson pensa che un limite all’evoluzione e’ l’abitabilità’ del pianeta. I nostri modelli fisico/matematici del Sole predicono che esso diventerà più brillante e che ad oggi ha aumentato la sua luminosità del 25% rispetto alla formazione del sistema solare. La nostra biosfera ha bisogno di temperature minori di 50 gradi per sopravvivere, il che suggerisce che la vita avrà “solo” un altro miliardo di anni a disposizione. Questo può sembrare un tempo molto lungo per la nostra scala temporale, ma se confrontato ai 4 miliardi di anni che la vita ha già superato sul nostro pianeta, si capisce che essa e’ nella parte finale della sua esistenza.
A. Watson sostiene che, se un pianeta e’ abitabile per un certo periodo di tempo, e la vita si sviluppa all’inizio di questo periodo, allora e’ probabile che l’evoluzione abbia avuto luogo anche su altri pianeti simili alla Terra. Comunque, siccome l’evoluzione e’ avvenuta sulla Terra solo nella parte finale del periodo di tempo dell’abitabilità’, A. Watson suggerisce che la nostra evoluzione e’ piuttosto improbabile.
Da un punto di vista matematico egli ha derivato le distribuzioni di probabilità di ogni evento cruciale dell’evoluzione. Il suo modello assume che i gradini dell’evoluzione sono intrinsecamente improbabili e che ognuno di essi può manifestarsi solo se i precedenti passi si sono verificati. Tutto il resto dell’evoluzione poi avviene molto rapidamente.
I passi critici vengono considerati degli eventi stocastici, con una probabilità uniforme anche se diversa.
La proprietà che essi sono intrinsecamente improbabili e’ espressa dalla condizione che il prodottoe’ molto minore di 1 dove th e’ il periodo medio dell’abitabilità’ del pianeta. La probabilità per unità di tempo che il primo passo avvenga e’ data da:
La probabilità congiunta sempre per unità di tempo che due eventi, uno al tempo t’ e il secondo a un tempo successivo t e’ data da:
La probabilità che il secondo evento si verifichi e’ ottenuta quindi da:
Continuando in questo modo, la probabilità che l’ennesimo evento si verifichi in sequenza ai precedenti n-1 passi si ottiene da:
dove K e’ un fattore di normalizzazione.
Usando le registrazioni dei fossili, Watson ha stimato un limite superiore per la probabilità che ogni passo critico si verifichi (10%) che fornisce una probabilità sull’emergenza della vita intelligente minore del 0.01% su 4 miliardi di anni.
Il lavoro sembra dar ragione all’ipotesi della Rare Earth che postula l’emergenza della vita complessa pluricellulare sulla Terra come una improbabile combinazione di eventi astrofisici, geologici e circostanze speciali. A. Watson, sostiene che l’intelligenza e’ ancora più improbabile della “semplice” vita e quindi ancora più improbabile.
Non c’e’ da stare molto allegri. Saremo per sempre destinati alla solitudine cosmica?
mercoledì 5 settembre 2012
Il grande freddo alla base della nascita del nostro Universo
venerdì 24 agosto 2012
Extraterrestri e numeri primi
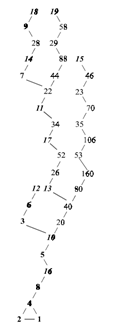
Come va interpretato questo messaggio? Esso consiste di 7 parti che codificano le seguenti informazioni:
1. I numeri da 1 a 10
2. I numeri atomici degli elementi presenti nel nostro DNA
3. Le formule dello zucchero e delle basi presenti nel DNA
4. Il numero di nucleotidi presenti nel DNA e un grafico della sua doppia elica
5. La figura di un uomo, l’altezza media di una persona e la popolazione della Terra
6. Un grafico del sistema solare
7. Un grafico del radiotelescopio di Arecibo e le dimensioni dell’antenna
(C5OH7) (C5H4N5) (C5H5N2O2) (C5OH7)
(PO4) (PO4)
(C5OH7) (C4H4N3O) (C5H4N5O) (C5OH7)
(PO4) (PO4)
I nucleotidi vengono raffigurati come sequenze di 5 atomi che rappresentano la formula della molecola.
Per esempio, nel caso della formula C5OH7, questa viene rappresentata nella parte in alto a sinistra dell’immagine e si legge come:
Le due colonne bianche di pixel ancora una volta vanno interpretate come sequenze di 1 e 0 dall’alto verso il basso.
Subito dopo viene riportato il sistema solare dove noi viviamo. Viene riportato il sole e i pianeti in base alla loro distanza da esso: Mercurio, Venere, Terra, Marte, Giove, Saturno, Urano, Nettuno e Plutone. Per evidenziare la Terra, da cui e’ stato inviato il messaggio, essa e’ stata rappresentata spostata in alto rispetto agli altri pianeti e subito sopra c’e’ la stilizzazione della figura umana.
E’ poi la volta della bellissima immagine del Telescopio da cui e’stato inviato il messaggio. Nella parte sottostante del telescopio in bianco, viene riportato in notazione binaria la dimensione del telescopio (306,18 m)
A questo punto non ci resta che riportare il messaggio per intero così come e’ stato inviato nello spazio. Ci risponderà mai nessuno? Credo che questa sia una domanda a cui difficilmente si potrà dare una risposta, almeno in tempi brevi.
Una cosa e’ certa: l’utilizzo dei numeri primi rende più semplici i messaggi da inviare nello spazio e allo stesso tempo piu’ difficili da decriptare quelli che viaggiano sulla Terra. E dire che fino a pochi anni fa, i numeri primi non erano altro che una semplice curiosità dei matematici.
domenica 29 luglio 2012
Un problema molto complesso – La congettura di Collatz
Consideriamo un qualsiasi numero intero positivo n.
- Se n e’ pari, lo dividiamo per 2
- Se n e’ dispari, lo moltiplichiamo per 3 e aggiungiamo 1.
Figura 1: Grafico dei tempi di arresto per i numeri da 2 a 9999.
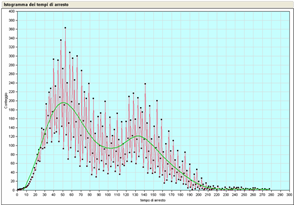
Figura 2: Distribuzione dei tempi di arresto per i numeri da 2 a 20000.
Figura 3: Grafico della sequenza di Collatz per il numero di partenza 27. Il tempo di arresto e’ di 111 passi.