Come il machine learning puo’ aiutare i geofisici nella predizione dei terremoti

 

Come residente della regione Abruzzo, una delle piu’ pericolose da un punto di vista sismico, e dopo aver vissuto il terremoto dell’Irpinia degli anni ottanta ho sperimentato sulla mia pelle la pericolosita’  di questo evento naturale che puo’ fare molti morti se ci trova impreparati.    

Se si riuscisse a prevedere quando avverra’ un terremoto, il popolo potrebbe prendere azioni preventive e si potrebbero salvare cosi potenzialmente molte vite. Con l’avvento del Machine Learning negli anni ottanta, i sismologi erano molto ottimisti e pensavano che prima o poi si sarebbe risolto il problema. Negli anni successivi purtroppo i sismologi hanno imparato che prevedere i terremoti e’ molto piu’ complicato di quanto pensavano a parte qualche dubbio risultato di scienza scadente come quello relativo al terremoto dell’Aquila o quelli riportati nel bel libro di Nate Silver “ The signal and the noise”.

Le onde generate da un terremoto sono composte da due tipi di onde: p-waves (onde di compressione) che viaggiano ad alta velocita’ e quindi meno dannose e le s-waves (onde di traslazione) che arrivano qualche secondo dopo le p-vawes e che generano i danni maggiori.

Rispetto agli anni ottanta il Machine Learning ha fatto molti passi avanti e c’e’ stato anche un aumento significativo dei dati raccolti sul campo e nei diversi laboratori del mondo; questo ha portato una nuova ventata di speranza di poter arrivare prima o poi alla previsione di questi eventi disastrosi.

In questo post cerco di descrivere proprio l’uso del machine learning nella modellizzazione di un set di dati pubblicati dai Laboratori di Los Alamos, ottenuti grazie ad un esperimento che cerca di mimare i terremoti reali.

L’esperimento e’ stato realizzato utilizzando  due presse idrauliche applicate a due lastre di acciaio con in mezzo uno strato granulare che allo stesso tempo viene spinto lentamente verso il basso. Dei sensori acustici catturano il suono generato dall’attrito del sistema generando in output un segnale digitale continuo (vedi immagine di seguito). Questo esperimento e’ una buona simulazione del movimento delle placche tettoniche vicino ad una linea di faglia, producendo dei terremoti ad un tasso  relativamente consistente. 

Il terremoto è un intenso scuotimento della superficie terrestre dovuto a un improvviso slittamento delle rocce nella crosta terrestre o a faglie vicino all'interfaccia tra le placche tettoniche. Il primo terremoto di cui si abbia notizia e’ quello verificatosi in Cina nel 1177 a.C. Il primo sismoscopio fu quello inventato dal filosofo cinese Chang Heng nel 132 d.C. Sebbene oggi il monitoraggio e la registrazione dei terremoti e’ un qualche cosa di ben sviluppato, non siamo ancora in grado di prevederli né di comprenderne la causa esatta. I terremoti tuttavia e le loro conseguenze sono tra gli eventi che di più hanno cambiato la vita nella storia dell'umanità. Le attività sismiche e le conseguenze dei disastri sono state la causa maggiore di  perdite di vite umane rispetto a tutti gli altri rischi naturali messi insieme negli ultimi due decenni, in quantro molti paesi si trovano in zone  sismicamente attive. L'approccio descritto in questo post combina il machine learning con metodi tipici delle serie temporali per stabilire  l'insieme di caratteristiche statistiche più adatte alla previsione del cosiddetto time to fail (TTF - il tempo rimanente prima di un sisma). Il database messo a disposizione dai Laboratori di Los Alamos consiste di due colonne e circa 630 milioni di righe.  Le due colonne del database hanno il seguente significato:

·   acoustic_data: il segnale acustico registrato in laboratorio durante l’esperimento;

·         time to failure TTF: il tempo rimanente in secondi prima che ci sia un terremoto.

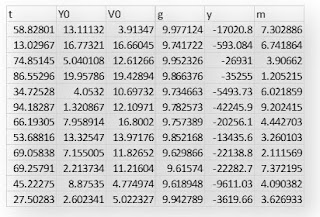
 Qui di seguito alcune righe del database in oggetto visualizzate con il software JMP Pro della SAS con cui verranno effettuate tutte le analisi successive. 

Nei due grafici seguenti viene riportato l’andamento del segnale acustico e il time to fail TTF dell’intero esperimento. Ci sono 16 terremoti in totale con time to fail che vanno da circa 16 sec a pochi secondi. 

Allo scopo di alleggerire il lavoro della CPU del mio PC ho considerato solo lo 0.025% dell’intero database campionato in modo casuale per non perdere l’informazione principale contenuto in esso. Evidenziati in nero due terremoti, l’ottavo e undicesimo della sequenza con i dati ridotti.

I dati acustici mostrano oscillazioni complesse con ampiezza variabile. Subito prima di ogni terremoto si verifica un aumento dell'ampiezza dei dati acustici. Grandi ampiezze si ottengono comunque anche in momenti diversi nel tempo e non sempre esattamente prima di un sisma. Questo lo possiamo vedere nel seguente grafico che riporta il segnale acustico dell’ottavo terremoto; le ampie oscillazioni visibili prima del sisma non avvengono proprio all'ultimo momento. Ci sono treni di oscillazioni intense che precedono il terremoto principale e altri con picchi più piccoli che lo seguono. Quindi, dopo alcune piccole oscillazioni, si verifica il terremoto.

Qui lo zoom sulla parte finale dell’ottavo terremoto. Come si diceva le oscillazioni dopo l’evento sismico sono molto piccole. 

 

Stessa cosa prima del terremoto indicato qui di seguito con una freccia: si notano molti segnali con picchi bassi prima dell’evento sismico. Questi picchi sono il risultato di eventi di micro fratture che possono essere utilizzati per predire il Time to fail (TTF).  In generale piu’ il TTF e’ corto e piu’ i picchi acustici sono frequenti. Le caratteristiche statistiche del segnale acustico quindi possono essere utilizzate come predittori per il modello di machine learning che andremo a sviluppare. 

La varianza del segnale acustico e’ la feature piu’ importante anche se altri parametri statistici come la kurtosis e la skewness non possono essere trascurati. Qui di seguito l’analisi temporale dell’ottavo terremoto eseguita con il modulo di time series di JMP Pro.

Si vede chiaramente che quando il tempo di fallimento tendo a zero (ci approssimiamo quindi all’evento sismico) c’e’ un aumento della variabilita’ del segnale acustico.  

Ovviamente per la costruzione di un modello predittivo non e’ possibile usare il solo segnale acustico fornito dal laboratorio di Los Alamos. Bisogna costruire delle nuove feature a partire dal dato acustico. Quest’attivita’ va sotto il nome di feature engineering. Si tratta di costruire delle nuove colonne (predittori) che possano aiutare l’algoritmo a fare le sue predizioni. Essendo il segnale una serie temporale possiamo usare la tecnica della moving window. In parole semplici a partire da un segnale se ne costruisce un altro calcolando una particolare statistica all’interno di una finestra di dimensione fissata e che si muove rigidamente di uno step alla volta. Supponiamo di avere i seguenti valori: 1 2 3 4 5. Possiamo pensare di costruire una finestra di dimensione 3. Partendo da 1 la finestra ingloba i valori 2, 3 e 4. Nell’ipotesi che siamo interessati alla media il valore sara’ (1+2+3+4)/4=2.5. Poi la finestra viene spostata di 1 e i valori al suo interno saranno: 2 3 4 5. Ricalcoliamo la media che questa volta sara’ 3.5 e cosi via. La finestra a partire da un certo valore della serie puo’ prevedere sia un certo numero di dati prima che dopo.    

Sono state costruite un totale di 18 caratteristiche statistiche. Dieci  di queste sono il massimo, minimo, media, mediana, deviazione standard, varianza, curtosi, moda, range e range interquartile. Le restanti otto caratteristiche sono i percentili a diversi valori: 1%, 5%, 10%, 25%, 75%, 90%, 95% e 99%.

Di seguito i grafici di alcune feature statistiche riportate in funzione del TTF per l’ottavo terremoto. E’ evidente come alcune caratteristiche correlino con il TTF, come per esempio la standard deviation, skewness e kurtosis.  

Nel grafico seguente viene riportato l’andamento della varianza per gli ultimi quattro terremoti contenuti nel database. Si vede come per questi c’e’ un trend a crescere della varianza del segnale acustico quanto il TTF si avvicina a zero (terremoto). Comunque da notare che alcune volte sono presenti delle spikes anche prima che avvenga il terremoto. In effetti dobbiamo pensare che durante il movimento delle placche terrestri iniziano a formarsi delle micro fratture nella crosta terreste la cui lunghezza determina l’intensita’ delle spikes. Col procedere dello slittamento si creeranno sempre piu’ microfratture fino a quando non si formera’ la frattura principale che potra’ essere lunga anche diversi chilometri. E’ un vero e proprio effetto domino.

L’algoritmo di machine learning che si e’ deciso di usare e’ il Random Forest.  Vediamo un attimo di cosa si tratta. Definito Bootstrap Aggregation (o Bagging in breve), è un metodo cosiddetto ensemble. Si tratta cioe’ di una tecnica che combina le previsioni di più algoritmi di apprendimento automatico per fare previsioni più accurate rispetto a qualsiasi singolo modello. Il bagging rientra nella categoria dell’apprendimento Ensemble e il nome deriva dalla combinazione Bootstrap e Aggregation. Il bootstrap indica il campionamento casuale con rimpiazzo del dataset iniziale. Se come modello individuale si decide di usare un decision tree allora l’algoritmo prende il nome di Random Forest. Ciò significa che una foresta casuale combina molti alberi decisionali in un unico modello. Individualmente, le previsioni fatte dagli alberi decisionali potrebbero non essere accurate, ma combinate insieme, le previsioni saranno in media più vicine al target. Il risultato finale restituito da un algoritmo di Random Forest altro non è che la media del risultato numerico restituito dai diversi alberi nel caso di un problema di regressione, o la classe restituita dal maggior numero di alberi nel caso di problemi di classificazione.

Prima di iniziare la modellizzazione si e’ provveduto alla creazione delle nuove features. Per la dimensione della finestra usata per la costruzione delle moving statistics sono stati scelti diversi valori come indicato di seguito:  

Window size: 20, 50, 100, 150, 300, 500

 Le prestazioni della Random Forest hanno mostrato una sensibile dipendenza dall’estensione della finestra temporale come riportato dalle tabelle statistiche  create in JMP per diversi modelli di RF.

L’R2, una delle possibili metriche utilizzate per misurare la bonta’ di un algoritmo mostra un chiaro trend a crescere all’aumentare della dimensione della finestra temporale considerata per la costruzione delle engineering features. Per le analisi mostrate di seguito si e’ scelto una dimensione della finestra di +/-1000.   

Cosi facendo si e’ ottenuto un R2 di circa 96% avendo utilizzato 100 decison tree nella foresta, un minimum split per albero pari a 10 e un numero di termini non superiore a 20.  

 Qui  l’andamento del TTF reale (in blu) e quello predetto (in rosso).

 Assegniamo adesso dei colori diversi al time to fail (TTF): dal rosso al verde man mano che mancano sempre meno secondi all’evento sismico. La parte colorata in viola rappresenta il cosiddetto after shock cioe’ quando il sistema ormai ha subito la frattura. Di norma questa parte andrebbe tolta dall’analisi in quanto ormai il terremoto e’ avvenuto. Notare infatti come quasi tutti i punti viola nel grafico del time predetto rispetto a quello actual si dispongono al di fuori della retta di correlazione.

Eliminando i dati dell’after shock le prestazioni della random forest migliorano ulteriormente dando un R2 del 98% e come predittori piu’ importanti quelli riportati nella tabella seguente.

 Ai primi posti abbiamo la standard deviation, i primi percentili, il minimo e il massimo e poi via via tutti gli altri. Considerando solo l’ottavo sisma possiamo vedere come esso evolve nel piano delle prime due componenti principali (PCA) che spiegano quasi il 70% dell’intera variabilita’ del sistema. Fino a pochi attimi prima del sisma il sistema si muove all’interno dello spazio identificato dall’ellisse di colore rosso. Nel momento della frattura principale il sistema fa un salto al di la dell’ellisse e si porta in una regione dello spazio mai visitata prima. Una volta rilasciata tutta la sua energia il sistema ritorna dove era partito e cioe’ all’interno dell’ellisse (seguire i colori del grafico per capire come evolve il terremoto). La parte verde indica quando avviene il terremoto mentre quella in viola indica il post terremoto. Questo andamento e’ vero per tutti i 16 terremoti contenuti nel database.  Il loading plot correttamente evidenzia un aumento dei valori di alcuni parametri quale il range, kurtosis, Skewness e varianza all’approssimarsi di un sisma.    

 

Qui viene riportata la sequenza del segnale acustico per i 16 terremoti del database iniziale.

Utilizzando una parte dei dati mai vista dal modello di Random Forest abbiamo eseguito la validazione dell’algoritmo necessaria per capire se il modello creato sta overfittando i dati. L’R2 medio ottenuto e’ di circa il 75% con una MAE di 2.18. Quest’ultimo indica il mean average error, cioe’ la somma del valore assoluto dei residui diviso il numero totale del campione. Come aspettato rispetto al data set usato come training le performance del modello sono inferiori. In questo caso abbiamo una differenza di circa il 22%. In definitiva il modello ha un Bias del 2% e una Variance del 22% che e’ decisamente ancora alta. In genere per ridurre la varianza ci sono diversi opzioni tra cui: 

 1. . aumentare la dimensione del campione

 2.    riduzione della complessita’ del modello   

Poiche’ nel seguente articolo “Machine learning predicts laboratory earthquakes, Geophysical Res. Letters 2017” utilizzando sempre una Random Forest con un centinaio di features e’ stato raggiunto un R2 di 89% sul test set c’e’ da aspettarsi che l’alta variance del nostro modello sia dovuta al campione limitato utilizzato per evitare di impegnare troppo la CPU del PC gia’ messa a dura prova col campione molto piccolo utilizzato rispetto all’originale.

Comunque anche se il risultato del test set non e’ stato dei migliori le informazioni ottenute sono comunque valide. L’utilita’ dell’applicazione del machine learning nella previsione del TTF dei Labmoti (terremoti generati in laboratorio) infatti sta nella possibilita’ di identificare dei segnali sconosciuti che possono portare a nuove conoscenze sulla fisica delle faglie. Cosa che e’ chiaramente deducibile anche dai risultati ottenuti nel nostro caso, che  fanno vedere come le intensita’ dei precursori sismici possono essere cosi basse che spesso potrebbero non essere registrate o addirittura non identificate. In passato infatti questi segnali scambiati per rumore venivano eliminati di proposito introducendo cosi un bias umano che invece nel machine learning e’ stato superato. Anche se il lavoro da fare rimane ancora tanto nella previsione dei terremoti della crosta terrestre di sicuro il ruolo del machine learning sara’ sempre piu’ importante e stimolante.        

Alla scoperta delle leggi di fisica con il machine learning

Nel lontano 1999, pubblicai sul TI Technical Journal (March 1999) un articolo scritto con alcuni miei colleghi dal titolo “Semiconductor Device Modeling using a Neural Network” (Link) in cui si proponeva l’uso di neural network (NN) per cercare di predire alcuni parametri critici dei dispositivi a semiconduttore partendo dai dati prodotti da un simulatore TCAD. Ma perche’ usare una NN per fare quello che puo’ fare un simulatore TCAD molto sofisticato e disponibile in tutti i centri di ricerca di grosse compagnie? Questione di memoria. Il CAD per produrre un risultato ha bisogno di tanta memoria e di tempi lunghi, addirittura di intere giornate. Una rete invece occupa poca memoria e una volta che ha appreso e’ velocissima. L’unica cosa importante e’ che con il simulatore bisogna esplorare uno “spazio delle fasi” del modello quanto piu’ largo e’ possibile,  all’interno del quale poi la rete fara’ le sue predizioni. Dopo 21 anni ritrovo in giro la stessa idea, allargata ovviamente a tutti gli algoritmi di machine learning e non solo le reti NN,  e applicata non solo nel campo dei semiconduttori ma ai concetti di base della fisica stessa. Procediamo con ordine.

Nelle ultime due decadi il Machine Learning e’ diventato uno dei pilastri dell’Intelligenza Artificiale, e parte della nostra vita anche se non tutti se ne accorgono. Il termine e’ stato usato per la prima volta da A. Samuel nel 1959. Ma quale e’ la differenza tra un algoritmo tradizionale e uno di machine elarning? Nel primo caso il programmatore conosce il modello e definisce i parametri e i dati necessari alla risoluzione del problema, mentre nel secondo caso non c’e’ un modello a priori e né una strategia. Si fa in modo che il computer impari da solo eseguendo l’attivita’ e migliorandola iterativamente. In questo caso si parla di apprendimento automatico. Con la continua crescita dei dati a disposizione e’ ragionevole pensare che la Data Analytics diventera’ sempre piu’ pervasiva e un ingrediente necessario del progresso tecnologico. Il Machine Learning puo’ apparire in diverse forme come:

1.     Ranking delle pagine web

2.     Identificazione di spamming

3.     Traduzione automatica

4.     Riconoscimento vocale

5.     Riconoscimento immagini

6.     Identificare gli interessi delle persone (come per es. su amazon, netflix etc)

per fare solo pochi esempi.  Il machine learning comunque e’ una tecnica molto potente non solo nel predire quale film ci piace vedere ma anche nella ricerca scientifica. Non a caso viene utilizzato su diversi siti web per la classificazione della forma delle galassie, l’individuazione delle tracce delle particelle elementari dopo una collisione, il riconoscimento di una forma tumorale dall’analisi di immagini TAC o della presenza di infezione da Covid-19 dall’analisi delle immagini a raggi X. E non solo. E’ notizia dell’ultima ora che il machine learning sta aiutando gli scienziati a predire i risultati di alcuni fenomeni naturali e in alcuni casi a rivelare le leggi alla base del fenomeno. Si avete capito bene, le leggi che sono alla base della natura. Pensate un attimo al racconto della mela di Netwon e supponete di trasferirlo nel mondo di oggi. Il nostro Netwon avra’ un cellulare, con cui potra’ organizzare l’esperimento della mela raccogliendo in una tabella l’altezza da cui cade la mela e il tempo necessario per arrivare a terra.  E supponiamo anche che Netwon abbia tanta pazienza da raccogliere ben 5000 misure. Questa potrebbe essere la tabella compilata. Il sistema di misure utilizzato e’ l’MKS cioe’ metri, Kg e secondi. Con y0 Newton ha indicato la posizione iniziale della mela cioe’ l’altezza da cui essa cade. La prima riga per esempio dice che la mela cadendo da un’altezza di 82 metri impiega 4 sec per arrivare a terra e cosi via.

  

 Ipotizziamo che Newton, uomo dei nostri tempi abbia a disposizione un software molto sofisticato per l’analisi dei dati e machine learning,  JMP Pro sviluppato dalla prestigiosa SAS. Tra i diversi modelli a disposizione e’ stata scelta una semplice rete neurale il cui schema e’ riportato qui di seguito:

Una rete neurale e’ un algoritmo che cerca di simulare il comportamento del nostro cervello. E’ costituita da uno strato di ingresso (il nostro y0) da alcuni strati nascosti (nel nostro caso 2, quelli con cerchi verdi) e uno strato di uscita (il nostro tempo t). Ogni strato e’ costituito da diversi nodi che rappresentano i nostri neuroni e delle linee che entrano ed escono da essi che simulano le nostre sinapsi. Ad ogni connessione e’ associato un peso che va a moltiplicare il valore che viene presentato su quel link. La stessa cosa accade per le altre connessioni. Dopo di che si sommano tutti i valori che insistono sullo stesso nodo. Questo costituisce il valore x di una funzione che viene specificata all’interno di ogni nodo (vedi immagine sopra dei cerchi verdi). Questa funzione viene chiamata funzione di attivazione. Tra quelle piu’ note abbiamo la funzione a gradino o sigmoide, quella lineare e quella Gaussiana. A seconda della funzione quindi avremo in uscita un certo valore dato da f(x)=y. 

  

 La potenza di questi oggetti, come per il nostro cervello sta nel mettere insieme piu’ nodi con connessioni non lineari tra loro. Questo costituisce una rete neurale. Dando alla rete sia i valori in input che in output, essa aggiusta in modo opportuno tutti i pesi delle connessioni per far si che l’errore in uscita sia il piu’ piccolo possibile. In partica si stabilisce una funzione di costo (anche detto Mean squared error - MSE) e si cerca dei metodi matematici per minimizzarla. Con la rete mostrata nell’immagine Diagram e con 5000 esempi raccolti dal nostro buon Netwon questo il risultato ottenuto.

Il campione a disposizione come vedete e’ stato diviso in 3 parti: un campione per il training, uno per la validation e un altro per il test.  Questo e’ vero per qualsiasi modello di machine learning utilizzato e non solo per le reti neurali. Questa divisione viene fatta per far si che la rete non impari a memoria perdendo cosi’ in generalizzazione della predizione. In effetti oltre al campione di training e di validazione dove la rete viene ottimizzata, si usa quello di test dove ci sono esempi che l’algoritmo non ha mai visto. Solo se le prestazioni della rete sono buone per entrambi il training e il test allora i suoi risultati si giudicano soddisfacenti. Nel nostro esempio i risultati sono eccezionali come ci dice il coefficiente R2 che e’ praticamente pari a 1 per tutti e 3 i gruppi. Ricordiamo che il parametro R2 esprime la bonta’ del nostro modello. Piu’ questo valore e’ vicino a 1 e piu’ il modello e’ buono. (per approfondimenti si puo’ consultare su questo blog il post ). Qui di seguito l’andamento previsto dalla rete della y0 e del tempo t. Come e’ possibile vedere la rete ha catturato correttamente l’andamento secondo la radice quadrata tra il tempo e l’altezza y0. 

Addirittura se andiamo a verificare il valore del tempo predetto in funzione dell’altezza y0 vediamo che la curva (in rosso) che meglio approssima i dati (in nero) e’ una radice quadrata e il coefficiente della radice quadrata di y0 e’ pari a 0.447 che e’ il valore previsto dalla teoria per l’accelerazione di gravita’.

Infatti la legge oraria della caduta dei gravi e’ data da:

Y=Yo+Vo*t-1/2*g*t^2

dove Yo e’ l’altezza, Vo la velocita’ iniziale e g l’accelerazione di gravita’, una costante pari a 9.8 m/sec2 in prossimita’ della superficie Terrestre. Per l’esperimento realizzato dal nostro Newton del 2020, Y=0 e Vo=0, cioe’

0=Yo-1/2*(9.8)*t^2

da cui

t=sqrt(Yo/5)=1/sqrt(5)*sqrt(Yo)=0.447*sqrt(Yo)  

avendo eliminata la soluzione negativa (in quanto il tempo e’ una quantita’ sempre positiva).

Adesso complichiamo leggermente le cose utilizzando l’intera legge oraria scritta precedentemente assumendo che la velocita’ iniziale non sia zero e che non ci sia un suolo su cui l’oggetto che cade possa fermarsi. Questo spiega i valori della y negativi nella tabella sottostante. I dati sono stati creati utilizzando la funzione RAND() di excel. Abbiamo introdotto anche una piccola variazione percentuale della costante g per cercare di confondere l’algoritmo. Come potete vedere e’ stata introdotta anche la massa m anche se dalla teoria sappiamo che essa non ha alcun impatto sulla caduta dei gravi come invece pensava Aristotele. Vediamo cosa succede utilizzando i predictive models di JMP Pro. 

Oltre alla rete neurale gia’ introdotta prima, sono stati utilizzati i seguenti modelli di machine learning: Random Forest (RF), Ensemble Boosted e KNN.

Prima di poter parlare di Random Forest dobbiamo introdurre il modello di decison tree da cui l’RF deriva. L’idea alla base dei modelli Tree e’ molto semplice. E’ quella dei mitici romani: dividi e governa. Dato un dataset con almeno una risposta Y (sia numerica che categorica) e tante features X (o anche predictors), l’algoritmo cerca di dividere il dataset in due gruppi per una certa X che massimizza la differenza tra i valori medi della Y nei due gruppi e che all’interno di ognuno di essi minimizza la standard deviation. Fatto cio’ ripete piu’ e piu’ volte questa divisione costruendo un vero e proprio albero con tanti rami e tante foglie (in giallo nell’immagine qui sotto).

 Purtroppo i decision tree sono molto sensibili ai dati in ingresso. Se i dati di training vengono cambiati (per esempio addestrando l’albero su un sottoinsieme dei dati di addestramento) l’albero decisionale risultante puo’ essere abbastanza diverso e con diverse previsioni.  Per questo motivo si e’ arrivati alle Random Forest (RF). Come il nome indica si tratta di un grande numero di alberi decisionali che operano come un tutt’uno nel senso che lavorano in parallelo. Le RF si basano sulla regola che un gruppo di persone e’ piu’ intelligente di un singolo individuo (saggio di J. Surowiecki, La saggezza della folla). Ogni singolo tree fa la sua previsione e la classe che ottiene piu’ voti diventa la previsione globale dell’algoritmo nel caso di classificazione oppure il valore medio nel caso di regressione. Individualmente, le previsioni fatte dai singoli alberi potrebbero anche essere non accurate, ma combinate insieme, si avvicineranno alla risposta corretta.

Passiamo adesso all’algoritmo di boosting. Come per le random forest anche questi modelli fanno parte dei cosiddetti modelli previsionali ottenuti tramite la composizione di vari modelli piu’ semplici (ensemble models). Il tutto nasce nel 1988 quando si capisce che un insieme di modelli di apprendimento deboli se messi insieme possono creare un modello robusto (l’unione fa la forza). Il concetto non e’ molto diverso dall’ottenere una funzione complessa a partire dalla somma di funzioni elementari semplici. Vediamo un esempio. Supponiamo di avere a disposizione dei dati (punti in blu nel grafico qui sotto) e vogliamo trovare la migliore curva che approssima questi punti. Poiche’ si vede un andamento globale a crescere la prima cosa che possiamo fare e’ provare con una funzione radice quadrata (in arancione). Non male. Osservando bene pero’ possiamo notare che ci sono delle oscillazioni intorno al valore della radice quadrata. Viene quindi spontaneo aggiungere alla radice quadrata una funzione seno (linea nera) che migliora l’approssimazione come si puo’ vedere dalla tabella excel riportata.

 

La somma dei residui al quadrato 

SUM(Y_actual-Y_predicted)^2

nel caso della radice quadrata e’ di circa 3800 mentre quella della funzione somma  

f(x)=a*sqrt(x)+b*(sin(c*x))                                                                a,b,c costanti

ha un valore di circa 200 cioe’ un fattore x19 di meno.

 E’ chiaro quindi che questo algoritmo lavora in serie cercando di migliorare un learner debole applicandone uno nuovo e cosi via. Allo stesso modo per un problema di classificazione o di regressione se M(x) e’ il primo modello avremo:

            Y=M(x)+e1                             con un’accuratezza per esempio pari a 84%

dove con e1 abbiamo indicato l’errore. Invece di procedere col costruire nuovi modelli, quello che si puo’ fare e’ cercare di modellizzare l’errore ottenendo qualche cosa come

e1=H(x)+e2

e a sua volta

e2=G(x)+e3

Se ci fermiamo qui otteniamo

Y=M(x)+H(x)+G(x)+e3

Arrivati qui possiamo assegnare degli opportuni pesi ai 3 learners M, G e H cercando di ottenere un’accuratezza migliore del primo learner M, cioe’

Y=aM(x)+bH(x)+cG(x)+e4                                                con Accuratezza>84%

L’ultimo modello utilizzato e’ il KNN cioe’ K-Nearest Neighbors model. Si tratta di uno dei modelli piu’ semplici del machine learning che produce dei buoni risultati in diverse situazioni. Si tratta di un algoritmo che cerca di predire una nuova istanza conoscendo i punti che sono separati in diverse classi. L’idea di base e’ quella di usare i k punti “piu’ vicini” (nearest neighbors) per effettuare la classificazione.

Questi algoritmi per poter lavorare correttamente hanno bisogno di una classe di training e di una metrica per calcolare la distanza (per esempio la distanza Euclidea) tra i vari records e il numero di vicini da utilizzare. Il processo di classificazione prima di tutto calcola la distanza rispetto ai record nel training set, identifica i k records piu’ vicini e utilizza le labels delle classe dei primi vicini per determinare la classe del record sconosciuto (per es. scegliendo quella che compare con maggiore frequenza) nel caso di classificazione oppure prendendo il valore medio dei primi vicini nel caso di regressione.  Qui di seguito un’immagine che mostra la definizione di primi vicini per diversi valori di k (da 1 a 3).

E’ chiaro che utilizzando valori diversi di k si otterranno risultati diversi come nel caso della regressione dove il valore medio dipende da quanti vicini vengono considerati. Bisogna quindi stabilire il valore ottimale di k. In genere l’errore per il gruppo di training e di validation ha un andamento come quello mostrato nell’immagine sottostante. Per piccoli valori di k l’errore sull’insieme di training e’ piccolo mentre quello sul validation set e’ grande. Chiaro segnale di overfitting nel senso che l’algoritmo ha una bassa generalizzazione della predizione avendo imparato a memoria. Al crescere di k vediamo che sia l’errore per il training set che per il validation set aumentano indicando che il modello e' in una condizione di underfitting. Comunque osservando la curva dell’errore del validation set (chiamata elbow a causa della sua forma a gomito) vediamo che essa mostra un minimo intorno a k=9. Questo valore di k e’ il valore ottimale del modello KNN.    

Dopo questo excursus sui modelli utilizzati, possiamo ritornare al nostro esperimento sintetico della caduta dei gravi. Utilizzando i 4 modelli descritti e presenti nel modulo di “Predictive modeling” di JMP Pro abbiamo ottenuto i seguenti risultati per la legge oraria del moto completa dei gravi. Il modello con le migliori prestazioni e’ stata la rete neurale seguita dal Boosted, dal KNN e per utlimo dal Random Forest. 

Osserviamo come la rete neurale (la stessa struttura di quella mostrata all’inizio di questo post) sia stata capace di prevedere l’andamento parabolico della y rispetto al tempo t.

Analizzando la sensibilta’ di ognuno dei parametri in X possiamo vedere come la rete abbia capito che la massa non ha alcun influenza sulla caduta di un corpo dando ragione a Newton e non ad Aristotele.

Interessante anche l’andamento della y con la g, l’accelerazione di gravita’ terrestre. Se questa diminuisce, come per esempio nel caso della luna, allora a parita’ di tempo t la y sara’ maggiore cioe’ il corpo avra’ percorso un tratto minore.   Altra osservazione.   Se guardiamo  al  grafico  che  mette in relazione  la y predetta  con quella  reale  si  puo’ vedere che se anche in termini di R2 i  3 modelli di NN,  Boosting e  KNN  sono molto simili essi  mostrano  una  varianza  intorno  alla  linea  centrale  diversa  con  la KNN essendo quella peggiore. 

Il modello della Random Forest e’ quella che merita un discorso a parte. Infatti e’ quello che mostra le performance peggiori in termini di R2. Proviamo a fare un grafico con i valori della y reali e quelli invece predetti dall’algoritmo. Notiamo subito che la retta e’ spezzata in due parti. Una pendenza piu’ o meno simile per i valori positivi e negativi con diversa intercetta. Anche considerando il valore assoluto della y questa anomalia rimane. Questo e’ un andamento che gli altri modelli non mostrano.

Passiamo adesso ad un altro fenomeno fisico molto noto, quello dell'interazione gravitazionale. Anche qui grazie a Newton sappiamo che la legge con cui due masse M1 e M2 si attirano dipende dalla loro distanza al quadrato secondo la legge:

F=-G (M1M2/r^2)

dove G e’ la costante gravitazione un numero uguale in tutti i punti dell’universo ed r la distanza tra le due masse. Come nei casi precedenti abbiamo generato 5000 records aggiungendo al data set una colonna V (velocita’) per cercare di “ingannare” il modello.

Esattamente come prima il miglior learner risulta essere la rete neurale, seguita dal modello Boosted, dal KNN e in ultimo dalle Random forest con una performance veramente poco convincente. 

Essendo l’R2 veramente molto basso si e’ provato a cambiare i parametri di default di JMP per migliorare l’R2. Uno di essi si e’ dimostrato essere quello giusto. Passando dal valore di default 2 a 5 siamo passati da un 47.7% al 91% come mostrato nella figura sottostante.  Il parametro in discussione e’ il numero di predittori che la foresta utilizza  ad ogni split. Avremo quindi una foresta che produce i suoi alberi considerando un solo predittore ad ogni split. Poi una seconda foresta che ne considerera’ 2 e cosi via fino a 5.  

Ancora una volta i learner sono riusciti a catturare il corretto andamento della legge fisica come possiamo vedere dall’andamento come 1/r^2 della forza F. E di nuovo i modelli hanno interpretato correttamente l’impatto nullo della velocita’ sulla forza F come stabilito dalla legge gravitazionale di Newton.

Questa la rete neurale utilizzata con due strati nascosti e tre diverse funzioni di attivazione.

  

Analizzare e comprendere i risultati dei diversi modelli di machine learning ancora richiede l’intervento umano essendo i risultati non chiari al pari di una legge matematica con tutta la sua eleganza e bellezza. Ma di sicuro essi possono aiutarci a capire come si comportano le leggi del nostro Universo semplicemente guardando nei dati, la ricchezza del futuro, il petrolio che fara’ muovere la tecnologia e la scienza dei prossimi anni. Pensate per esempio alla possibilita’ di applicare il machine learning a problemi complessi come quelli dei 3 corpi o all’ipotesi di Riemann sugli zeri della funzione zeta per citarne solo alcuni.