Nel lontano 1999, pubblicai sul TI Technical
Journal (March 1999) un articolo scritto con alcuni miei colleghi dal titolo “Semiconductor
Device Modeling using a Neural Network” (Link) in cui si proponeva l’uso di neural network (NN) per cercare di predire alcuni parametri critici dei dispositivi a
semiconduttore partendo dai dati prodotti da un simulatore TCAD. Ma perche’
usare una NN per fare quello che puo’ fare un simulatore TCAD molto sofisticato
e disponibile in tutti i centri di ricerca di grosse compagnie? Questione di
memoria. Il CAD per produrre un risultato ha bisogno di tanta memoria e di
tempi lunghi, addirittura di intere giornate. Una rete invece occupa poca
memoria e una volta che ha appreso e’ velocissima. L’unica cosa importante e’ che
con il simulatore bisogna esplorare uno “spazio delle fasi” del modello quanto
piu’ largo e’ possibile, all’interno del
quale poi la rete fara’ le sue predizioni. Dopo 21 anni ritrovo in giro la stessa
idea, allargata ovviamente a tutti gli algoritmi di machine learning e non solo
le reti NN, e applicata non solo nel
campo dei semiconduttori ma ai concetti di base della fisica stessa. Procediamo
con ordine.
Nelle ultime due decadi il Machine Learning e’
diventato uno dei pilastri dell’Intelligenza Artificiale, e parte della nostra
vita anche se non tutti se ne accorgono. Il termine e’ stato usato per la prima
volta da A. Samuel nel 1959. Ma quale e’ la differenza tra un algoritmo
tradizionale e uno di machine elarning? Nel primo caso il programmatore conosce
il modello e definisce i parametri e i dati necessari alla risoluzione del
problema, mentre nel secondo caso non c’e’ un modello a priori e né una
strategia. Si fa in modo che il computer impari da solo eseguendo l’attivita’ e
migliorandola iterativamente. In questo caso si parla di apprendimento
automatico. Con la continua crescita dei dati a disposizione e’ ragionevole pensare
che la Data Analytics diventera’ sempre piu’ pervasiva e un ingrediente
necessario del progresso tecnologico. Il Machine Learning puo’ apparire in
diverse forme come:
1.
Ranking delle
pagine web
2.
Identificazione
di spamming
3.
Traduzione
automatica
4.
Riconoscimento
vocale
5.
Riconoscimento
immagini
6.
Identificare gli
interessi delle persone (come per es. su amazon, netflix etc)
per fare solo pochi esempi. Il machine learning comunque e’ una tecnica
molto potente non solo nel predire quale film ci piace vedere ma anche nella
ricerca scientifica. Non a caso viene utilizzato su diversi siti web per la
classificazione della forma delle galassie, l’individuazione delle tracce delle
particelle elementari dopo una collisione, il riconoscimento di una forma
tumorale dall’analisi di immagini TAC o della presenza di infezione da Covid-19
dall’analisi delle immagini a raggi X. E non solo. E’ notizia dell’ultima ora
che il machine learning sta aiutando gli scienziati a predire i risultati di
alcuni fenomeni naturali e in alcuni casi a rivelare le leggi alla base del
fenomeno. Si avete capito bene, le leggi che sono alla base della natura.
Pensate un attimo al racconto della mela di Netwon e supponete di trasferirlo
nel mondo di oggi. Il nostro Netwon avra’ un cellulare, con cui potra’
organizzare l’esperimento della mela raccogliendo in una tabella l’altezza da cui
cade la mela e il tempo necessario per arrivare a terra. E supponiamo anche che Netwon abbia tanta pazienza
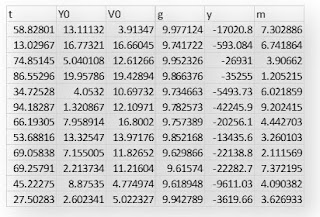
da raccogliere ben 5000 misure. Questa potrebbe essere la tabella compilata. Il
sistema di misure utilizzato e’ l’MKS cioe’ metri, Kg e secondi. Con y0 Newton
ha indicato la posizione iniziale della mela cioe’ l’altezza da cui essa cade.
La prima riga per esempio dice che la mela cadendo da un’altezza di 82 metri impiega
4 sec per arrivare a terra e cosi via.
Una rete neurale e’ un algoritmo che cerca di simulare il
comportamento del nostro cervello. E’ costituita da uno strato di ingresso (il
nostro y0) da alcuni strati nascosti (nel nostro caso 2, quelli con cerchi
verdi) e uno strato di uscita (il nostro tempo t). Ogni strato e’ costituito da
diversi nodi che rappresentano i nostri neuroni e delle linee che entrano ed
escono da essi che simulano le nostre sinapsi. Ad ogni connessione e’ associato
un peso che va a moltiplicare il valore che viene presentato su quel link. La
stessa cosa accade per le altre connessioni. Dopo di che si sommano tutti i
valori che insistono sullo stesso nodo. Questo costituisce il valore x di una
funzione che viene specificata all’interno di ogni nodo (vedi immagine sopra
dei cerchi verdi). Questa funzione viene chiamata funzione di attivazione. Tra
quelle piu’ note abbiamo la funzione a gradino o sigmoide, quella lineare e
quella Gaussiana. A seconda della funzione quindi avremo in uscita un certo
valore dato da f(x)=y.
La potenza di questi oggetti, come per il nostro cervello
sta nel mettere insieme piu’ nodi con connessioni non lineari tra loro. Questo costituisce
una rete neurale. Dando alla rete sia i valori in input che in output, essa
aggiusta in modo opportuno tutti i pesi delle connessioni per far si che
l’errore in uscita sia il piu’ piccolo possibile. In partica si stabilisce una
funzione di costo (anche detto Mean squared error - MSE) e si cerca dei metodi
matematici per minimizzarla. Con la rete mostrata nell’immagine Diagram e con
5000 esempi raccolti dal nostro buon Netwon questo il risultato ottenuto.
Il campione a disposizione come vedete e’ stato diviso in
3 parti: un campione per il training, uno per la validation e un altro per il
test. Questo e’ vero per qualsiasi
modello di machine learning utilizzato e non solo per le reti neurali. Questa
divisione viene fatta per far si che la rete non impari a memoria perdendo
cosi’ in generalizzazione della predizione. In effetti oltre al campione di
training e di validazione dove la rete viene ottimizzata, si usa quello di test
dove ci sono esempi che l’algoritmo non ha mai visto. Solo se le prestazioni
della rete sono buone per entrambi il training e il test allora i suoi
risultati si giudicano soddisfacenti. Nel nostro esempio i risultati sono
eccezionali come ci dice il coefficiente R2 che e’ praticamente pari a 1 per tutti
e 3 i gruppi. Ricordiamo che il parametro R2 esprime la bonta’ del nostro
modello. Piu’ questo valore e’ vicino a 1 e piu’ il modello e’ buono. (per
approfondimenti si puo’ consultare su questo blog il post ). Qui
di seguito l’andamento previsto dalla rete della y0 e del tempo t. Come e’
possibile vedere la rete ha catturato correttamente l’andamento secondo la
radice quadrata tra il tempo e l’altezza y0.
Addirittura se andiamo a verificare il valore del tempo
predetto in funzione dell’altezza y0 vediamo che la curva (in rosso) che meglio
approssima i dati (in nero) e’ una radice quadrata e il coefficiente della
radice quadrata di y0 e’ pari a 0.447 che e’ il valore previsto dalla teoria
per l’accelerazione di gravita’.
Infatti la legge oraria della caduta dei gravi e’ data da:
Y=Yo+Vo*t-1/2*g*t^2
dove Yo e’ l’altezza, Vo la velocita’ iniziale e g l’accelerazione di
gravita’, una costante pari a 9.8 m/sec2 in prossimita’ della superficie Terrestre.
Per l’esperimento realizzato dal nostro Newton del 2020, Y=0 e Vo=0, cioe’
0=Yo-1/2*(9.8)*t^2
da cui
t=sqrt(Yo/5)=1/sqrt(5)*sqrt(Yo)=0.447*sqrt(Yo)
avendo eliminata la soluzione negativa (in quanto il
tempo e’ una quantita’ sempre positiva).
Adesso complichiamo leggermente le cose utilizzando
l’intera legge oraria scritta precedentemente assumendo che la velocita’
iniziale non sia zero e che non ci sia un suolo su cui l’oggetto che cade possa
fermarsi. Questo spiega i valori della y negativi nella tabella sottostante. I
dati sono stati creati utilizzando la funzione RAND() di excel. Abbiamo
introdotto anche una piccola variazione percentuale della costante g per
cercare di confondere l’algoritmo. Come potete vedere e’ stata introdotta anche
la massa m anche se dalla teoria sappiamo che essa non ha alcun impatto sulla
caduta dei gravi come invece pensava Aristotele. Vediamo cosa succede
utilizzando i predictive models di JMP Pro.
Oltre alla rete neurale gia’ introdotta prima, sono stati
utilizzati i seguenti modelli di machine learning: Random Forest (RF), Ensemble Boosted e KNN.
Prima di poter parlare di Random Forest dobbiamo
introdurre il modello di decison tree da cui l’RF deriva. L’idea alla base dei
modelli Tree e’ molto semplice. E’ quella dei mitici romani: dividi e governa.
Dato un dataset con almeno una risposta Y (sia numerica che categorica) e tante
features X (o anche predictors), l’algoritmo cerca di dividere il dataset in
due gruppi per una certa X che massimizza la differenza tra i valori medi della
Y nei due gruppi e che all’interno di ognuno di essi minimizza la standard deviation. Fatto cio’ ripete piu’ e piu’ volte questa divisione costruendo un
vero e proprio albero con tanti rami e tante foglie (in giallo nell’immagine
qui sotto).
Purtroppo i decision tree sono
molto sensibili ai dati in ingresso. Se i dati di training vengono cambiati
(per esempio addestrando l’albero su un sottoinsieme dei dati di addestramento)
l’albero decisionale risultante puo’ essere abbastanza diverso e con diverse
previsioni. Per questo motivo si e’
arrivati alle Random Forest (RF). Come il nome indica si tratta di un grande
numero di alberi decisionali che operano come un tutt’uno nel senso che
lavorano in parallelo. Le RF si basano sulla regola che un gruppo di persone e’
piu’ intelligente di un singolo individuo (saggio di J. Surowiecki, La saggezza
della folla). Ogni singolo tree fa la sua previsione e la classe che ottiene
piu’ voti diventa la previsione globale dell’algoritmo nel caso di
classificazione oppure il valore medio nel caso di regressione. Individualmente,
le previsioni fatte dai singoli alberi potrebbero anche essere non accurate, ma
combinate insieme, si avvicineranno alla risposta corretta.
Passiamo adesso all’algoritmo di
boosting. Come per le random forest anche questi modelli fanno parte dei
cosiddetti modelli previsionali ottenuti tramite la composizione di vari
modelli piu’ semplici (ensemble models). Il tutto nasce nel 1988 quando si capisce
che un insieme di modelli di apprendimento deboli se messi insieme possono
creare un modello robusto (l’unione fa la forza). Il concetto non e’ molto
diverso dall’ottenere una funzione complessa a partire dalla somma di funzioni
elementari semplici. Vediamo un esempio. Supponiamo di avere a disposizione dei
dati (punti in blu nel grafico qui sotto) e vogliamo trovare la migliore curva
che approssima questi punti. Poiche’ si vede un andamento globale a crescere la
prima cosa che possiamo fare e’ provare con una funzione radice quadrata (in
arancione). Non male. Osservando bene pero’ possiamo notare che ci sono delle
oscillazioni intorno al valore della radice quadrata. Viene quindi spontaneo
aggiungere alla radice quadrata una funzione seno (linea nera) che migliora
l’approssimazione come si puo’ vedere dalla tabella excel riportata.
La somma dei residui al
quadrato
SUM(Y_actual-Y_predicted)^2
nel caso della radice quadrata e’
di circa 3800 mentre quella della funzione somma
f(x)=a*sqrt(x)+b*(sin(c*x)) a,b,c costanti
ha un valore di circa 200 cioe’
un fattore x19 di meno.
E’ chiaro quindi che questo algoritmo lavora
in serie cercando di migliorare un learner debole applicandone uno nuovo e cosi
via. Allo stesso modo per un problema di classificazione o di regressione se
M(x) e’ il primo modello avremo:
Y=M(x)+e1 con
un’accuratezza per esempio pari a 84%
dove con e1 abbiamo indicato
l’errore. Invece di procedere col costruire nuovi modelli, quello che si puo’
fare e’ cercare di modellizzare l’errore ottenendo qualche cosa come
e1=H(x)+e2
e a sua volta
e2=G(x)+e3
Se ci fermiamo qui otteniamo
Y=M(x)+H(x)+G(x)+e3
Arrivati qui possiamo assegnare
degli opportuni pesi ai 3 learners M, G e H cercando di ottenere un’accuratezza
migliore del primo learner M, cioe’
Y=aM(x)+bH(x)+cG(x)+e4 con Accuratezza>84%
L’ultimo modello utilizzato e’ il
KNN cioe’ K-Nearest Neighbors model. Si tratta di uno dei modelli piu’ semplici
del machine learning che produce dei buoni risultati in diverse situazioni. Si
tratta di un algoritmo che cerca di predire una nuova istanza conoscendo i
punti che sono separati in diverse classi. L’idea di base e’ quella di usare i
k punti “piu’ vicini” (nearest neighbors) per effettuare la classificazione.
Questi algoritmi per poter
lavorare correttamente hanno bisogno di una classe di training e di una metrica
per calcolare la distanza (per esempio la distanza Euclidea) tra i vari records
e il numero di vicini da utilizzare. Il processo di classificazione prima di
tutto calcola la distanza rispetto ai record nel training set, identifica i k
records piu’ vicini e utilizza le labels delle classe dei primi vicini per
determinare la classe del record sconosciuto (per es. scegliendo quella che
compare con maggiore frequenza) nel caso di classificazione oppure prendendo il
valore medio dei primi vicini nel caso di regressione. Qui di seguito un’immagine che mostra la
definizione di primi vicini per diversi valori di k (da 1 a 3).
E’ chiaro che utilizzando valori
diversi di k si otterranno risultati diversi come nel caso della regressione
dove il valore medio dipende da quanti vicini vengono considerati. Bisogna
quindi stabilire il valore ottimale di k. In genere l’errore per il gruppo di
training e di validation ha un andamento come quello mostrato nell’immagine
sottostante. Per piccoli valori di k l’errore sull’insieme di training e’
piccolo mentre quello sul validation set e’ grande. Chiaro segnale di
overfitting nel senso che l’algoritmo ha una bassa generalizzazione della
predizione avendo imparato a memoria. Al crescere di k vediamo che sia l’errore
per il training set che per il validation set aumentano indicando che il
modello e' in una condizione di underfitting. Comunque osservando la curva dell’errore del
validation set (chiamata elbow a causa della sua forma a gomito) vediamo che
essa mostra un minimo intorno a k=9. Questo valore di k e’ il valore ottimale
del modello KNN.
Dopo questo excursus sui modelli
utilizzati, possiamo ritornare al nostro esperimento sintetico della caduta dei
gravi. Utilizzando i 4 modelli descritti e presenti nel modulo di “Predictive
modeling” di JMP Pro abbiamo ottenuto i seguenti risultati per la legge oraria
del moto completa dei gravi. Il modello con le migliori prestazioni e’ stata la
rete neurale seguita dal Boosted, dal KNN e per utlimo dal Random Forest.
Osserviamo come la rete neurale (la stessa struttura di quella mostrata
all’inizio di questo post) sia stata capace di prevedere l’andamento parabolico
della y rispetto al tempo t.
Analizzando la sensibilta’ di ognuno dei parametri in X
possiamo vedere come la rete abbia capito che la massa non ha alcun influenza sulla
caduta di un corpo dando ragione a Newton e non ad Aristotele.
Interessante anche l’andamento della y con la g,
l’accelerazione di gravita’ terrestre. Se questa diminuisce, come per esempio
nel caso della luna, allora a parita’ di tempo t la y sara’ maggiore cioe’ il
corpo avra’ percorso un tratto minore. Altra osservazione. Se guardiamo al grafico che mette in relazione la y predetta con quella reale si puo’ vedere
che se anche in termini di R2 i 3 modelli di NN, Boosting e KNN sono molto
simili essi mostrano una varianza intorno alla linea centrale diversa con la
KNN essendo quella peggiore.
Il modello della Random Forest e’ quella che merita un
discorso a parte. Infatti e’ quello che mostra le performance peggiori in
termini di R2. Proviamo a fare un grafico con i valori della y reali e quelli
invece predetti dall’algoritmo. Notiamo subito che la retta e’ spezzata in due
parti. Una pendenza piu’ o meno simile per i valori positivi e negativi con
diversa intercetta. Anche considerando il valore assoluto della y questa
anomalia rimane. Questo e’ un andamento che gli altri modelli non mostrano.
Passiamo adesso ad un altro fenomeno fisico molto noto, quello dell'interazione gravitazionale. Anche qui grazie a Newton sappiamo che la legge con cui due masse M1 e M2 si attirano dipende dalla loro distanza al quadrato secondo la legge:
F=-G
(M1M2/r^2)
dove G e’ la costante gravitazione un numero uguale in
tutti i punti dell’universo ed r la distanza tra le due masse. Come nei casi
precedenti abbiamo generato 5000 records aggiungendo al data set una colonna V
(velocita’) per cercare di “ingannare” il modello.
Esattamente come prima il miglior learner risulta essere
la rete neurale, seguita dal modello Boosted, dal KNN e in ultimo dalle Random
forest con una performance veramente poco convincente.
Essendo l’R2 veramente molto basso si e’ provato a
cambiare i parametri di default di JMP per migliorare l’R2. Uno di essi si e’
dimostrato essere quello giusto. Passando dal valore di default 2 a 5 siamo
passati da un 47.7% al 91% come mostrato nella figura sottostante. Il parametro in discussione e’ il numero di
predittori che la foresta utilizza ad
ogni split. Avremo quindi una foresta che produce i suoi alberi considerando un
solo predittore ad ogni split. Poi una seconda foresta che ne considerera’ 2 e
cosi via fino a 5.
Ancora una volta i learner sono riusciti a catturare il
corretto andamento della legge fisica come possiamo vedere dall’andamento come
1/r^2 della forza F. E di nuovo i modelli hanno interpretato correttamente
l’impatto nullo della velocita’ sulla forza F come stabilito dalla legge
gravitazionale di Newton.
Questa la rete neurale utilizzata con due strati nascosti e tre
diverse funzioni di attivazione.
Analizzare
e comprendere i risultati dei diversi modelli di machine learning ancora
richiede l’intervento umano essendo i risultati non chiari al pari di una legge
matematica con tutta la sua eleganza e bellezza. Ma di sicuro essi possono
aiutarci a capire come si comportano le leggi del nostro Universo semplicemente
guardando nei dati, la ricchezza del futuro, il petrolio che fara’ muovere la
tecnologia e la scienza dei prossimi anni. Pensate per esempio alla
possibilita’ di applicare il machine learning a problemi complessi come quelli
dei 3 corpi o all’ipotesi di Riemann sugli zeri della funzione zeta per citarne
solo alcuni.
























Nessun commento:
Posta un commento