Il primo a proporre questa congettura e’ stato Lothar Collatz nel 1937, da cui ha preso il nome. La congettura e’ anche conosciuta come il problema 3n+1. La sequenza di numeri coinvolti e’ riferita come la sequenza dei chicchi di grandine (hailstone sequence in inglese).
Questa congettura e’ cosi complicata da dimostrare, che il grande genio matematico Paul Erdos, un giorno disse che la matematica ancora non era pronta per risolvere un tale problema. Ma vediamo da vicino in che cosa consiste questa congettura.
Consideriamo un qualsiasi numero intero positivo n.
Consideriamo un qualsiasi numero intero positivo n.
- Se n e’ pari, lo dividiamo per 2
- Se n e’ dispari, lo moltiplichiamo per 3 e aggiungiamo 1.
Se eseguiamo queste operazioni ripetutamente, prendendo come ingresso, il risultato dell’operazione precedente, si raggiunge sempre il numero 1 indipendentemente dal numero di partenza n.
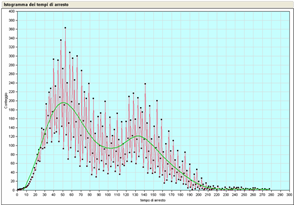
Il numero di passi impiegati per arrivare ad 1 e’ detto il tempo totale di arresto del numero n (total stopping time in inglese). Nella figura 1 vengono riportati i tempi di arresto di tutti i numeri interi tra 2 e 9999, mentre nella figura 2 la frequenza con cui ogni tempo di arresto si presenta per valori di n tra 2 e 20000.
Figura 1: Grafico dei tempi di arresto per i numeri da 2 a 9999.
Osservare che ci sono due picchi a circa 50 e 135 con oscillazioni che si accentuano nell’intorno di questi due picchi e che si smorzano verso le due code della distribuzione.
Figura 2: Distribuzione dei tempi di arresto per i numeri da 2 a 20000.
Ovviamente la congettura di Collatz e’ equivalente ad affermare che per ogni n ci sia un tempo di arresto finito. Nel caso in cui esistesse un numero n che non arriva mai ad 1, perché entra in un loop non contenente 1 o perché cresce senza limite, allora la congettura di Collatz risulterebbe falsa.
Partendo, per esempio, col numero n=6, la sequenza per arrivare al punto fisso 1 prende 8 passi 6, 3, 10, 5, 16, 8, 4, 2, 1, con n=11 ci vogliono 14 passi, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 e per n=27 ci vogliono ben 111 passi prima di arrivare ad 1, toccando numeri al di sopra di 9000 per poi discendere verso il suo attrattore. (vedi figura 3).
Figura 3: Grafico della sequenza di Collatz per il numero di partenza 27. Il tempo di arresto e’ di 111 passi.
Qui di seguito il grafo diretto dei primi 20 numeri. Osservare come la sequenza di Collatz converge sempre al loop 4-2-1.
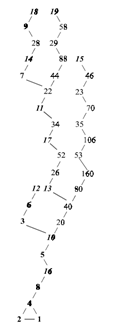
La congettura, tramite l’utilizzo massiccio dei computer, e’ stata provata essere vera fino a 2.88×1018. Anche se questo numero e’ molto grande, non significa che la congettura e’ vera. Ci sono state altre congetture che si sono dimostrate false solo per valori veramente grandi.
Utilizzando comunque un approccio di tipo probabilistico, la congettura sembra essere vera. Considerando infatti, un numero intero dispari a caso si può verificare che in media la crescita aspettata della sequenza fino al numero dispari successivo e’ pari a 3/4 e quindi minore di 1. Questo dovrebbe comportare che ogni sequenza di Collatz dovrebbe decrescere man mano che si sviluppa. Ma questo dovrebbe provare solo che la sequenza eventualmente non diverge. Ma e’ sempre possibile che essa entri in un ciclo in cui non e’ presente l’uno. Quindi punto e a capo. Sono solo ipotesi e purtroppo fino a quando non arriverà una dimostrazione o un contro esempio rimaranno tali.
La congettura di Collatz ad oggi rimane irrisolta.
Sebbene il problema sia molto semplice da spiegare e da capire, la natura della congettura e il comportamento di questo sistema dinamico rende enormemente difficile provare o confutare la congettura.
Nel 1985 Lagarias cosi scriveva in merito alla congettura di Collatz:
La difficoltà del problema 3n+1 sembra essere legata al fatto che si tratta di un processo deterministico che simula un comportamento casuale (randomico). I metodi esistenti in Teoria dei numeri non sembrano essere adatti per la soluzione della congettura. In questo senso il problema ad oggi, sembra essere intrattabile.





Noi del piccolo gruppo "B.Riemann" abbiamo già proposto sul nostro sito una dimostrazione della congettura di Collatz, (3n+1)/2, con una variante (4n+5)/3, ed altre estensioni sarebbero possibili (ma con relativi numeri di Collatz sempre più rari e quindi con cicli numerici sempre molto più lunghi rispetto alla nota versione più piccola (3n+1)/2. Il problema è che tale congettura, comprese estensioni, non serve a granchè (solo in matematica ricreativa)per cui l'abbiamo abbandonata al suo destino, per dedicarci a cose più utili e interessanti. Per esempio, di recente, ai numeri di Landau , di forma n^2 +1 (infiniti), mentre i numeri di forma n^2 -1 non sono mai numeri primi perchè sempre prodotti di due numeri che differiscono di 2 (caso particolare i numeri primi gemelli): Ma anche di altri argomenti di teoria dei numeri. Buona lettura!
RispondiEliminaFrancesco
Come posso entrare nel sito?
EliminaDimenticavo: anche nelle estensioni della congettura di Collatz, i cicli numerici, sia pure sempre più lunghi (per via della sempre maggiore distanza tra i relativi numeri di Collatz per ogni estensione) sono sempre finiti, cioè prima o poi terminano sempre, poichè incappano in un qualsiasi numero di Collatz per ogni estensione (i numeri di Collatz sì che sono infiniti). Il segreto stà nei quandrati dispari di 2, di 3, ecc. Nella congettura di Collatz nota,(3n+1)/2, abbiamo che 3+1 = 4 = 2^2 (il 2 a denominatore), mentre per la nostra estensione (4n+5)/3 abbiamo invece 4+5 = 9 = 3^2 (il 3 a denominatore), ma altre estensioni sono possibili,per esempio (16n + 9 )/5 in questo caso 16 + 9 = 25 =5^2, ma lasciamo agli appassionati l'approfondimento di questa possibile estensione della congettura di Collatz.Ovviamente, tali estensioni sono infinite, poichè ci sono infiniti numeri ed infiniti quadrati, alla base del funzionamento di qualsiasi estensione.
RispondiEliminaAttendiamo possibili sviluppi... Francesco
Rettifica: per errore ho scritto quadrati dispari di 2, invece si tratta di quadrati pari di 2, o meglio ancora di 4; ogni ciclo numerico comincia sempre la sua fine quando incontra un numero di Collatz, di forma 4^m -1/3, e cioè, nell'ordine, 1=(4-1), 5=(16 -1)/3; 21 =(64 -1)/3, ecc. Se si incontra per es. il 5, come in qualcuno degli esempi, 5*3 +1 = 16, ed essendo 16 una potenza di 2, il ciclo collassa verso la fine perchè 16/2=8, 8/2= 4, 4/2 =2, 2/2 =1, fine del ciclo. Le potenze di 2 sono tutte ovviamente divisibili continuamente per 2 e non si incontrano più numeri dispari, tranne l' 1 finale, numero di Collatz; e ricominciando da 1, abbiamo infatti 1*3 *1 = 4, 4/2=2 2 2/2 = 1. Francesco
RispondiEliminasi potrebbe anche dire che la funzione Sommatoria (4^n) con n=0; n appartiene ad N; restituisce tutti i progressivi numeri di Collatz.
EliminaOppure ottenere gli stessi valori applicando l'algoritmo (4n+1) con valore iniziale di n=0; lo stesso algoritmo può essere utilizzato per trovare tutti i numeri che danno origine ad un termine dispari dato, ad esempio se (3*3+1)/2 = 5, per conoscere tutti i dispari che (tralasciando i valori pari della Hailstone) mi portano a 5, basta porre n=3 come valore iniziale.
paul spider
Per eventuali interessati, anche ad altri argomenti e problemi di teoria dei numeri e numeri primi, il nostro sito, con breve descrizione, è il seguente:
RispondiElimina“In questo sito http://nardelli.xoom.it/virgiliowizard/, vengono pubblicati saltuariamente articoli vertenti principalmente sulle varie e possibili connessioni tra alcuni settori della teoria dei numeri (serie di Fibonacci e numero aureo, numeri primi e funzione zeta, gruppi eccezionali di Lie, partizioni di numeri) e le teorie di stringa e/o fenomeni naturali connessi; ma, seppure con minore frequenza, anche articoli su congetture circa la fattorizzazione veloce, sull’ipotesi di Riemann e su ipotesi RH - equivalenti (o su problemi minori della teoria dei numeri (per es. congettura di Goldbach, dei numeri primi gemelli, di Collatz, dei numeri di Sophie Germain con relativa generalizzazione ecc. ecc.)."
A tutti, buona lettura! Francesco
Ho letto l'articolo di Nardelli. Non si tratta di una vera dimostrazione della congettura. Il fatto che leggendo a ritroso ogni sequenza si incontri sempre un numero di Collatz non implica che, al contrario, qualunque sequenza partente da un numero n incontri un numero di Collatz .
RispondiEliminaCon l'algoritmo di Collatz come con qualunque algoritmo, non è possibile elaborare tutti i numeri naturali perché non sappiamo: quantità e valori dei numeri pari e dispari e non conosceremo mai tutti i loro fattori. Dal triangolo di Tartaglia possiamo rilevare i numeri dispari che sono la somma dei risultati delle infinite potenze di 2 che hanno indice pari e che sono anche uguali al precedente dispari * 4 + 1. Questi sono tutti i numeri dispari che * 3 + 1 genera un numero pari che è il risultato di una potenza di base 2 e di un indice pari 2 ^ (2 * n≥1) e che, l'ennesima metà, termina a 1 perché ½ di 2 ^ 1 = 2 ^ 0 = 1. cordialità https://vixra.org/abs/2112.0004
RispondiElimina