dove
e’ chiamato l’esponente di Lyapunov. Notare che per tempi
l’amplificazione di fluttuazioni microscopiche e’ cosi’ spinta che la prevedibilita’ di qualsiasi traiettoria individuale e’ completamente impossibile.
Ma cosa possiamo dire riguardo al nostro sistema solare? Si tratta di un sistema dinamico stabile? E’ possibile per esempio, predire il moto di un singolo pianeta per i prossimi miliardi di anni?
Essendo il sistema solare, un sistema con molti gradi di liberta’ (9 pianeti piu’ il sole che moltiplicato per i 3 gradi di liberta’ di ognuno fanno 30 gradi di liberta’) e’ chiaro che ci si aspetta un sistema dinamico caotico. E questo in effetti e’ il risultato ottenuto di recente dal team del ricercatore Laskar, che con delle simulazioni numeriche molto accurate, e’ riuscito a stimare un tempo di Lyupanov per l’intero sistema solare di circa 5 milioni di anni. Questo significa che un’incertezza iniziale di 1 Km sulla posizione iniziale di un pianeta, puo’ arrivare ad un’unita astronomica (AU=1.5E+8 Km) dopo 95 milioni di anni.
Il fatto che l’esponente di Lyapunov non e’ molto grande, significa che il sistema solare non ha un alto grado di caoticita’, dovuto alla possibilita’ di trascurare l’interazione gravitazionale tra i pianeti rispetto a quella tra i pianeti e il sole. Come esempio di esponente di Lyapunov, nella figura 1, viene riportata la divergenza tra due orbite di Plutone inizialmente molto vicine al trascorrere degli anni.
Figura 1: La divergenza d (in unita’ astronomiche) tra due orbite di Plutone inizialmente vicine, cresce esponenzialmente nel tempo (in milioni di anni). Il fit lineare dei dati, comporta un tempo di Lyupanov dell’ordine dei 10 milioni di anni.
Gli studi al computer della storia caotica del sistema solare, sono diventati un ramo molto importante ed interessante della fisica non-lineare, che hanno aperto nuove possibilita’ per la comprensione delle orbite dei pianeti del sistema solare e di altre stelle. In effetti, ci sono state speculazioni sulla struttura numerica delle orbite dei pianeti, fin dal diciottesimo secolo, quando J. Titius e J. Bode notarono una relazione regolare tra le distanze medie dei pianeti dal sole come indicato nella Tabella 1. Ponendo la distanza Terra-Sole uguale ad un’unita’ astonomica (AU), la regola di Titius-Bode e’ data da:
dove a e’ la distanza media del pianeta dal sole in AU ed n e’ il numero planetario che corrisponde a 0 per Venere e per Mercurio. Questa formula riusci’ a predire con buona approssimazione la posizione di Urano, scoperto nel 1781, cioe’ 9 anni dopo la formulazione della regola. Tuttavia per Nettuno e Plutone scoperti successivamente, la formula di Titius-Bode si e’ dimostrata essere non precisa e questo ha fatto si che diversi studiosi, hanno elaborato una versione piu’ recente capace di predire non solo le distanze di Nettuno e Plutone ma anche dei satelliti di Giove, Saturno ed Urano. L’accordo tra le distanze predette e quelle osservate per i vari satelliti e’ qualche cosa di eccezionale con degli errori di alcuni per cento. La versione recente della legge di Titius-Bode e’ data da:
con k una costante uguale a 0.21363 AU e
Ultimamente, sempre il ricercatore Laskar e il suo team, usando una combinazione di tecniche numeriche ed analitiche, ha scoperto la seguente relazione, valida non solo per il sistema solare ma anche per i pianeti extrasolari recentemente scoperti:
dove a, come sempre e’ la distanza media dal sole, n il numero planetario e k una costante. Laskar ha trovato k=0.14 per i pianeti interni del sistema solare e 0.81 per i pianeti esterni.
Tabella 1: Distanze medie planetarie dal sole in unita’ astonomiche e corrispondenti valori della regola di Titius-Bode, dei risultati di Laskar e del modello quantistico di Nottale.
Sia la legge di Titius-Bode che i calcoli numerici di Laskar, suggeriscono un qualche ordine sottostante, una qualche regolarita’ celeste paragonabile a quella dell’atomo di idrogeno prima della versione quantizzata di Bohr e Schroedinger. Proprio da questo tipo di osservazioni e’ partita l’analisi del gruppo di uno studioso francese, Laurent Nottale, che ha congetturato che le traiettorie degli elettroni negli atomi e i pianeti del sistema solare su una scala temporale maggiore di 0.1 miliardi di anni subiscono una sorta di moto Browniano, che e’ continuo ma non differenziabile, come il perimetro di una curva di Koch o di una costa marina. Essi hanno proposto una teoria per calcolare le probabilita’ delle orbite planetarie che da un punto di vista formale sono identiche a quelle della meccanica quantistica formulate da Schroedinger e Bohr per le orbite elettroniche negli atomi, nonostante l’utilizzo di parametri completamente diversi. Come per il caso dei raggi delle orbite elettroniche dell’atomo di idrogeno, proporzionali al quadrato di n, Laurent Nottale e il suo gruppo ritiene che le distanze medie dei pianeti siano date da:
dove n e’ l’indice orbitale e alfa una costante di proporzionalita’ per i pianeti interni (indicata col pedice i) ed esterni (indicata col pedice o).
Poiche’ per i pianeti interni risulta
e l’indice di Mercurio e’ uguale a 3, questo significa che c’e’ la possibilita’ di due pianeti interni molto vicini al Sole, molto probabilmente evaporati dal calore del Sole o uno evaporato (quello piu’ vicino al Sole) e l’altro ancora da scoprire. La costante dei pianeti esterni, invece, e’ pari a 1.125 AU. La relazione di Nottale e’ in ottimo accordo con i dati misurati, compresi gli asteroidi piu’ grandi, i satelliti dei pianeti del sistema solare e anche di molti dei pianeti extrasolari (vedi figura 2).
Ma questi risultati sono delle idee credibili da un punto di vista scientifico o si tratta di semplice numerologia? Al momento e’ difficile dirlo. Solo le osservazioni di altri pianeti extrasolari ed extragalattici, ed ulteriori studi teorici in quest’area potranno fornire, una risposta definitiva. Al momento lasciamoci sorprendere dalla grande efficacia della matematica nel descrivere tutto cio’ che ci circonda dall’infinitamente piccolo all’infinitamente grande.
Figura 2: Radice quadrata del rapporto (a/M) con a in AU ed M in masse solari in funzione dell’intero n, per i pianeti interni del sistema solare e alcuni pianeti extrasolari scoperti da poco.
Appunti di viaggio di un fisico curioso...... della bellezza di tutto quello che ci circonda,dell'irragionevole efficacia della matematica nello spiegare il mondo intorno a noi, della continua lotta della vita tra ordine e caos, curioso dell'emergenza della complessita' da regole elementari e tant'altro....... Sara' un viaggio divertente e spero ricco di sorprese.
domenica 11 novembre 2012
L’armonia planetaria
Il grande scienziato Laplace, era convinto che se avessimo potuto conoscere la posizione e la velocita’ iniziale di tutti i corpi presenti nel cosmo, saremmo riusciti a predire con esattezza il futuro e il passato dell’Universo. Se questa affermazione risultasse vera, conoscendo le masse, le velocita’ e le posizioni di tutti i corpi del sistema solare, sarebbe possibile determinare le loro traiettorie per tempi arbitrariamente lunghi. La descrizione del moto dei pianeti, ha stimolato da sempre la mente di diversi scienziati. Scoperte decisive nella determinazione delle leggi fisiche che governano il moto dei pianeti sono state fatte da scienziati del calibro di Copernico, Galileo, Keplero e Newton. Nonostante tutti gli sforzi, ad oggi la meccanica celeste dei due corpi (per esempio il sistema terra-sole) e’ l’unica ben sviluppata e compresa, mentre il problema dei tre o piu’ corpi (per esempio sole-terra-luna) e’ molto complesso. Esso, infatti non ammette soluzioni analitiche, e l’unica possibilita’ rimane quella di ricorrere a metodi numerici. Anche la versione semplificata del modello, il cosiddetto problema dei tre corpi ristretto, in cui la massa di uno dei corpi e’ trascurabile rispetto alla massa totale del sistema, puo’ esibire delle dinamiche molto complesse, nel senso che piccole variazioni nelle condizioni iniziali possono portare a differenze significative nelle traiettorie future dei corpi. In questo caso si parla di sistema dinamico caotico. Indicando con , una piccolissima differenza tra due condizioni iniziali, in un sistema dinamico caotico, la differenza al tempo t, tra le due traiettorie inizialmente molto vicine sara’ determinata dalla relazione
Iscriviti a:
Commenti sul post (Atom)

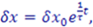








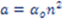




Nessun commento:
Posta un commento