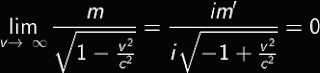Un’altra prova a sfavore dei neutrini superluminali

La saga dei neutrini superluminali continua. E un’ulteriore prova si aggiunge a quella dei giorni scorsi pubblicata anche su questo blog. Questa volta la prova viene da un altro esperimento sui neutrini sempre presso il Gran Sasso chiamato ICARUS. Questo esperimento come OPERA ha rivelato i neutrini “sparati” dal CERN sin dal 2010 (Link).

Ora se i neutrini rivelati da OPERA fossero realmente superluminali, secondo due scienziati della Boston University, Cohen e Glashow (premio Nobel per la Fisica nel 1979) questi dovrebbero perdere la loro energia durante i 730 Km che separano il CERN dal Gran Sasso, producendo coppie di elettroni e positroni, in modo analogo alla luce Cherenkov emessa quando una particella attraversa un mezzo ad una velocita’ superiore a quella della luce nel mezzo stesso. Essa e’ la causa del colore azzurrino delle piscine in cui sono immersi i reattori nucleari.

La produzione di coppie elettroni/positroni con relativa perdita di energia dovrebbe deformare lo spettro energetico dei neutrini in arrivo al Gran Sasso. Ed e’ proprio questa pertubazione che non e’ stata osservata in un anno di dati prodotti da ICARUS confutando cosi’ l’ipotetica osservazione di neutrini superluminali del team di OPERA. 

Vediamo i dettagli. Secondo l’osservazione di Cohen e Glashow, i neutrini superluminali dovrebbero emettere della radiazione a causa della presenza delle Interazioni Deboli. In particolare l’emissione di elettroni e positroni dovrebbe avvenire ad una energia data da:

dove

e’ il valore identificato da OPERA, m la massa dell’elettrone, c la velocita’ della luce e v la velocita’ dei neutrini.

Questo fa si che la soglia di energia sia di circa 140 MeV.

Secondo i calcoli effettuati dai due scienziati dell’Universita’ di Boston (Link) l’energia finale dei neutrini dopo aver percorso una distanza L avendo un’energia iniziale Ei dovrebbe essere data da:

dove k e’ una costante. Osserviamo che una volta stabilita la distanza L (nel nostro caso 730 Km), conoscendo l’energia iniziale dei neutrini e misurando quella finale e’ possibile ricavare la differenza tra la velocita’ dei neutrini e quella della luce   o viceversa assumendo un certo valore di delta e conoscendo L e l’energia iniziale dei neutrini e’ possibile predire l’energia finale dei neutrini e confrontarla con quella misurata.

L’esperimento ICARUS consiste di 760 tonnellate di argon liquido super-puro che opera come una camera a bolle  registrando tutti gli eventi che depositano un’energia superiore alle centinaia di MeV all’interno di una finestra di 60 us centrata intorno all’impulso di neutrini inviato dal CERN. 

                                                               Esperimento ICARUS

L’apparato e’ capace di rivelare i neutrini muonici inviati dal CERN grazie all’interazioni di quest’ultimi con gli atomi di argon che producono una particolare traccia che dipende dall’energia del muone che viene creato da queste interazioni.

                                                   Tipico evento registrato da ICARUS.         

Misurando l’angolo theta mostrato nella figura precedente  e’ possibile ricostruire l’energia del muone che ha creato il segnale. Da quando e’ entrato in funzione, ICARUS, ha registrato circa 100 eventi di questo tipo, non tantissimi ma sufficienti per costruire lo spettro di energia dei muoni (in blu) e confrontarlo con quello aspettato (linea rossa).  

A partire dai dati del muone e’ possibile ricostruire la distribuzione energetica dei neutrini (cioe’ l’istogramma dell’energia o in altre parole quanti neutrini arrivano con una data energia) “sparati” dal CERN (in blu) e  confrontarla con quella aspettata dalle simulazioni (linea rossa).

Come si puo’ vedere dalla figura l’accordo tra i dati sperimentali e quelli aspettati e’ molto buono.  

Come detto all’inizio del post, secondo i calcoli di Cohen e Glashow, se i neutrini viaggiassero ad una velocita’ superiore a quella della luce come OPERA sembra indicare, allora la loro distribuzione di energia dovrebbe apparire distorta; in particolare per un delta nell’intervallo indicato da  OPERA

(5E-5), l’energia media dei neutrini dovrebbe essere di circa 15 GeV contro i ~28 osservati da ICARUS e inoltre non ci dovrebbe essere nessun evento ad energia  superiore  a ~15 GeV (vedi linea in viola nella figura sottostante).  Ma cosi non e’. Ci sono tanti eventi al di sopra di ~15 GeV e in media i neutrini hanno una energia ben superiore a quella prevista da Cohen e Glashow nel caso essi viaggiassero ad una velocita’ superluminale.

                                                    (da http://scienceblogs.com/startswithabang/)

Sempre secondo la teoria di Cohen e Glashow, nel caso in cui i neutrini fossero superluminali, dovrebbero perdere la loro energia emettendo coppie elettroni-positroni e quindi arrivare con un’energia media pui’ bassa al Gran Sasso (15 GeV contro i ~28 GeV) che avrebbe comportato l’osservazione di una distribuzione di energia dei muoni (linea in violetto) molto diversa da quella osservata (punti blu).

Si tratta di una differenza enorme specialmente ad energie superiori ai 15 GeV. Quindi i dati di ICARUS in modo inequivocabile mostrano un’inconsistenza sostanziale con quelli di Opera. Ulteriore conferma di un qualche possibile errore fatale fatto dal Team di OPERA.

Non ci resta che rimandare ad un futuro prossimo la possibilita’ di trovare nel nostro universo delle particelle tachioniche.   

Neutrini piu’ veloci della luce? Forse trovato l'errore

Alcune settimane fa quando i responsabili dell’esperimento Opera hanno pubblicato i risultati della loro ricerca sulla velocita’ dei neutrini sembrava che alcune delle leggi fondamentali della fisica venissero messe duramente alla prova. 

La stampa e i vari blog hanno dato grande risalto alla notizia con titoli che sembravano mettere in discussione la relativita’ di Einstein.

In questi ultimi giorni, invece proprio la relativita’ di Einstein sembra rimettere tutto in discussione grazie ad una ricerca di alcuni scienziati che hanno spiegato il perche’ dei 60 ns di differenza trovati da Opera rispetto al valore aspettato.  

L’elevata velocita’ dei neutrini e la relativa distanza non molto grande tra il CERN e il Gran Sasso, significa dover conoscere con estrema precisione la distanza tra la sorgente (CERN) e il rivelatore (Gran Sasso) nonche’ l’istante in cui i neutrini lasciano la sorgente e quello in cui arrivano al rivelatore (il tempo impiegato dai neutrini per coprire la distanza CERN-Gran Sasso si chiama tempo di volo). 

Durante l’esperimento Opera, sembra che i ricercatori che hanno usato i GPS  per misurare la distanza e il tempo di volo abbiano dimenticato di considerare una variabile fondamentale: la relativita’ appunto.

E’ quello che emerge dallo studio del ricercatore  Ronald A.J. van Elburg dell'Università di Groningen, in Olanda che ha scritto un articolo in cui spiega come  “gli effetti della relativita’ richiedono 2 correzioni alle misure del tempo di volo dei neutrini”.

Queste correzioni alterano il tempo di volo dei neutrini di ~64 ns facendo si che la velocita’ dei nuetrini, all’interno degli errori di misura, sia uguale a quella della luce.

Comunque Van Elburg non e’ il solo scienziato che sta lavorando alla verifica dei risultati dell’esperimento Opera.  In 3 settimane dopo l’annuncio del CERN ci sono stati piu’ di 80 articoli pubblicati sul server arxiv per spiegare i possibili errori fatti durante l’esperimento dei neutrini.

Mentre alcuni scienziati cercano di spiegare il risultato di Opera ricorrendo ad una nuova fisica, come i neutrini che viaggiano attraverso dimensioni extra, o neutrini che viaggiano ad una velocita’ superiore a quella della luce ma solo a particolari energie, altri cercano spiegazioni meno rivoluzionarie cercando eventuali errori nei dati dell’esperimento.  

Vediamo adesso in dettaglio i risultati di Van Elburg.

Come tutti sanno, l’esperimento di Michelson e Morley,  ha dimostrato che la velocita’ della luce e’ la stessa in tutti i sistemi inerziali, e su questo assioma Einstein costrui’ la relativita’ speciale. Anche se la velocita’ della luce e’ invariante rispetto ad un cambio di sistema di riferimento inerziale, la relativita’ speciale non preserva la distanze e il tempo separatamente. Infatti affinche’ la velocita’ della luce sia costante in tutti i sistemi di riferimento e’ necessario correggere la distanza e il tempo con il cosiddetto fattore di trasformazione di Lorentz. In aggiunta la descrizione di eventi  e’  diversa a seconda dei sistemi di riferimento, in altre parole un cambio di prospettiva comporta un diverso scenario.  

Questo cambiamento di scenario diventa importante se vogliamo calcolare la velocita’ di una particella usando una sorgente A e un rivelatore B separati da una distanza fissa Sb nel sistema di riferimento solidale con la Terra e utilizzando un orologio che invece si muove con una velocita’ v dalla sorgente A verso il rivelatore B. Ma perche’ l’orologio si muove verso B?

Il tempo di volo e’ un parametro molto difficile da misurare. Il team di Opera riporta che è riuscito a calibrare con estrema precisione i due istanti importanti per la misurazione sintonizzando gli orologi presenti ad ogni capo dell'esperimento.
Sono riusciti a fare cio’  grazie ai satelliti GPS. Ognuno dei satelliti trasmette un segnale molto accurato dall'orbita, a circa 20 km di altezza. Questo comunque introduce una serie di complicazioni che il team ha dovuto considerare, come il tempo necessario al segnale per arrivare sulla terra.

E' facile pensare che il moto dei satelliti sia irrilevante. Dopo tutto, le onde radio che portano il segnale  viaggiano alla velocità della luce, a prescindere dalla velocità dei satelliti. Ma c'è un'ulteriore sottigliezza da considerare. Anche se la velocità della luce non dipende dal sistema di riferimento, il tempo di volo dei neutrini si. In questo caso, ci sono due sistemi di riferimento: l'esperimento sulla terra e gli orologi in orbita. Se questi si muovono uno rispetto all’altro allora questo va tenuto in considerazione.

Dal punto di vista di un orologio a bordo di un satellite GPS, la posizione della sorgente dei neutrini al CERN e quella del rivelatore al Gran sasso, cambia continuamente. "Dalla prospettiva dell'orologio, il rivelatore si muove verso la sorgente e di conseguenza, la distanza percorsa dai neutrini, misurata dal sistema di riferimento dell’orologio, è più corta" ha spiegato van Elburg. Ovviamente con questo intende che la distanza è più corta della distanza misurata nel sistema di riferimento a terra.

Calcoliamo il tempo di volo di particelle come i fotoni, che viaggiano alla velocita’ della luce da A in B, nel sistema di riferimento dell’orologio in orbita e confrontiamolo con quello misurato da un sistema di riferimento sulla Terra.

La distanza Sc tra la sorgente A e il rivelatore B nel sistema di riferimento in orbita e’ legata alla distanza misurata nel sistema di riferimento solidale con la Terra Sb tramite il fattore di Lorentz:

Da un punto di vista dell’orologio in orbita il rivelatore B si muove verso la sorgente A ad una velocita’ v. E quindi la distanza Sc sara’ coperta dai fotoni in un tempo nel sistema di riferimento dell’orologio dato da:

Da queste due relazioni ricaviamo che:

Nel sistema di riferimento solidale con la Terra invece il tempo impiegato dai fotoni per percorrere la distanza Sb non e’ dato da:

  come assunto dal team di Opera ma da:

 

 

La differenza tra questi due tempi  e’ data da:

 

 

Per calcolare questo valore abbiamo bisogno di ricavare la velocita’ del satellite GPS. Questa e’ data da:

dove R e’ la distanza tra il centro della Terra e il satellite e T il periodo di rotazione del satellite intorno alla Terra. R sara’ dato dalla somma del raggio terrestre piu’ l’altezza del satellite dalla superfice della Terra, cioe:

I satelliti GPS considerati nell’esperimento Opera orbitano da Ovest ad Est lungo un piano inclinato a 55 gradi rispetto all’equatore con un periodo di 11 h 58 min cioe’ circa 12 ore.  

Questo fa si che la velocita’ sia uguale a:

Sapendo che la distanza tra A e B e’ di:

e che:

otteniamo un valore di epsilon uguale a 32 ns. In altre parole il tempo di volo osservato e’ di 32 ns piu’ corto di quello trovato se avessimo usato un orologio solidale con la terra.

Tempo, che va raddoppiato perché lo stesso effetto vale ad ogni capo dell'esperimento. Quindi la correzione totale è di 64 nanosecondi, quasi esattamente quello che il team di OPERA ha osservato. Questa analisi del prof. Van Elburg è davvero un risultato notevole anche se il problema non è ancora da considerarsi chiuso. Come sempre nella scienza, serviranno ulteriori verifiche sia dei risultati dell'esperimento OPERA che di questa e altre pubblicazioni che verranno. Alla fine si andra’ in una direzione o nell’altra  solo ed esclusivamente in base alle prove ottenute.

Se la tesi di Van  Elburg risultera’ essere decisiva, l’esperimento Opera non solo non avrà evidenziato una falla nella teoria della Relatività di Einstein, ma sarebbe un ulteriore prova a sua favore.

Neutrini superluminali?

La notizia dei risultati dell’esperimento OPERA del Gran Sasso e’ di quelle che fara’ discutere a lungo il mondo dei fisici. La sua portata e’ cosi sconvolgente che potrebbe richiedere la riscrittura di una parte della fisica. Ecco perche’ da piu’ parti c’e’ un invito alla prudenza. Solo dopo avere rivisto attentamente tutti i dati prodotti da OPERA (che potrebbe richiedere anche anni) la comunita’ scientifica potra’ dare il suo verdetto definitivo. Ma che cosa e’ OPERA?

OPERA e’ l’acronimo di Oscillation Project with emulsion-tRacking apparatus, un esperimento nato per analizzare i neutrini inviati dal Super proton synchrotron del CERN di Ginevra. Il fascio di neutrini attraversa la crosta terrestre e dopo un viaggio di circa 732 Km arriva al laboratorio del gran Sasso dove i neutrini vengono catturati dai rivelatori di OPERA.

Come lo stesso acronimo indica, OPERA non e’ nato per misurare la velocita’ dei neutrini ma per cercare di confermare le cosiddette oscillazioni dei neutrini. Queste particelle fantasma quasi prive di massa esistono in 3 diversi sapori (elettronico, muonico e tauonico) e solo da qualche anno sappiamo che mentre viaggiano cambiano sapore in accordo con una previsione del fisico italiano Bruno Pontecorvo, uno dei componenti del team di Enrico Fermi.

Ma lo stesso apparato puo’ misurare anche la velocita’ dei neutrini. Infatti utilizzando la semplice formula:

conoscendo la distanza d e il tempo di volo tra il CERN e il gran Sasso si puo’ ricavare la velocita’ v. Ovviamente la misura di queste due quantita’ deve essere effettuata con un livello di confidenza elevato. Sapendo che la velocita’ della luce c e’ di 300000 Km/sec e che la distanza d e di circa 730 Km, ci aspettiamo un tempo di volo di 730/300000=0.00243.. sec, cioe’ di circa 2.4 ms. Invece i neutrini rilevati da OPERA “sembra” che abbiano impiegato un tempo di solo 60 nanosecondi piu’ corto, cioe’ 6 miliardesimi di secondo in meno. Fin qui sembra tutto facile. Ma non e’ cosi. Visto che stiamo parlando di tempi cosi’ corti c’e’ bisogno di misure molto precise sia della distanza percorsa che dei tempi di volo. Tenendo conto degli errori sistematici e di quelli statistici i 60 nanosecondi misurati sono affetti da un errore di circa 10 ns. Questo significa che la deviazione tra il tempo atteso e quello misurato e’ circa 6 volte l’errore. Basterebbe un errore leggermente piu’ grande per ridurre significativamente questo margine e quindi la probabilita’ che i neutrini viaggino ad una velocita’ superiore a quella della luce. Ecco perche’ i fisici hanno accettato con molto prudenza questo risultato. Tra l’altro questa non e’ la prima volta che vengono fatte misure della velocita’ dei neutrini. Gia’ nel 2007, l’esperimento americano Minos aveva trovato risultati simili anche se con una confidenza piu’ bassa. Usando un fascio di neutrini da 3 GeV avevano riportato una misura relativa della velocita’ dei neutrini di:

contro un valore di

di OPERA che usa neutrini da 17 GeV. Non solo. Nel 1987 un gruppo di astrofisici aveva trovato un limite alla velocita’ relativa inferiore a due miliardesimi usando gli antineutrini provenienti dalla supernova SN1987A. Ma in questo caso i neutrini avevano un energia di solo 10 MeV. E’ possibile che la velocita’ dei neutrini possa dipendere dalla loro energia? Al momento nessuno lo sa. Detto questo, che implicazioni avrebbe questo risultato se venisse confermato? Prima di tutto credo che non sia del tutto esatto dire (come quasi tutte le notizie di queste ore riportano) che la teoria di Einstein sia da mettere in discussione. La relativita’ si basa su un postulato che piu’ o meno dice che la velocita’ della luce e’ la stessa per tutti gli osservatori. Essa e’ invariante rispetto agli osservatori inerziali. Inoltre sempre secondo la relativita’ di Einstein la velocita’ della luce e’ una velocita’ limite. Ma come tutti i limiti e’ possibile tendere ad un punto di accumulazione sia da destra che da sinistra. Questo significa che un qualsiasi oggetto nel nostro Universo si puo’ trovare in 3 diversi regimi di velocita’:

Tutte le particelle che hanno una massa a riposo diversa da zero hanno velocita’ inferiore a quella della luce e le uniche ad avere la velocita’ della luce sono quelle con massa a riposo nulla come i fotoni, i quanti della radiazione elettromagnetica. Ma perche’ una particella con massa diversa da zero non puo’ essere accelerata da zero fino alla velocita’ della luce?

Come sappiamo dalla relativita’ di Einstein, una particella con massa a riposo m e ferma rispetto ad un sistema di riferimento ha un’energia data dalla famosissima formula di Einstein:

Se la particella e’ in moto vale invece la seguente relazione:

dove mγ e’ la massa relativistica della particella. Da questa relazione si puo’ capire perche’ non e’ possibile accelerare una particella fino alla velocita’ della luce. Per v che si avvicina a c, il denominatore dell’equazione precedente tende a zero e l’energia totale all’infinito. Ecco svelato l’arcano. Per accelerare una particella da zero alla velocita’ della luce c’e’ bisogno di una energia infinita perche’ la massa relativistica diventa infinita. Ma il fatto che non e’ possibile accelerare una particella alla velocita’ della luce non significa che non possano esistere delle particelle che fin dalla loro nascita abbiano avuto sempre una velocita’ maggiore di quella della luce. E’ la stessa cosa che dire che i fotoni viaggiano sempre alla velocita’ della luce e che non possono fermarsi mai e non sono mai stati accelerati a quella velocita’. Sono semplicemente nati cosi e cosi moriranno. Particelle con velocita’ superiori a quella della luce sono state ipotizzate teoricamente gia’ anni fa e sono state chiamate tachioni o particelle superluminali. Le particelle del nostro universo invece vengono chiamate tardioni.

Quindi i neutrini potrebbero essere le prime particelle superluminali ad essere state individuate nel nostro Universo. Ma allora perche’ tanto rumore? Perche’ purtroppo i tachioni sono degli oggetti molto bizzarri a cui i fisici non hanno mai creduto realmente. Intanto, dovrebbero avere una massa immaginaria. Si avete capito bene. Una massa quadrata negativa. Questo perche’ se v e’ maggiore di c nell’equazione dell’energia relativistica la quantita’ a denominatore sotto la radice quadrata e’ negativa e questo comporta un numero immaginario.Per far si che l’energia sia una quantità reale bisogna assumere che la massa sia una quantita’ immaginaria, cioe’ una quantita’ pari a i*m il cui quadrato e’ una quantita’ negativa essendo il quadrato di i uguale a -1 (dalle nozioni fondamentali della matematica complessa). Riportando il fattore gamma in funzione della velocita’ v e assumendo la velocita’ della luce pari a 1, si ottiene il grafico riportato sotto.

Nella regione viola, al di sotto della velocita’ della luce si vede chiaramente che quando una particella e’ a riposo il fattore gamma e’ uguale all’unita’ mentre esso tende all’infinito quando la velocita’ si avvicina a quella della luce. Nella regione verde invece (quella dei tachioni), quando la velocita’ e’ superiore a quella della luce si osserva una cosa molto strana. Il fattore gamma e quindi l’energia della particella diventa sempre piu’ piccola man mano che la velocita’ diventa sempre piu’ grande mentre tende all’infinito quando cerchiamo di frenare la particella. Questo e’ esattamente il contrario di quello che vediamo tutti i giorni sotto i nostri occhi. Un mondo veramente strano quello dei tachioni.  

Osserviamo che solo assumendo una massa immaginaria fa si che l’energia sia una quantita’ reale reale essendo il rapporto tra due immaginari un numero reale.

E non finisci qui. Nel mondo fantastico dei tachioni, succederebbero cose molto strane con il principio di causa-effetto. In parole molto semplici i tachioni potrebbero viaggiare all’indietro nel tempo.

Conviene fermarsi qui per non rischiare di entrare nel mondo della fantascienza. Dovrebbe essere chiaro a tutti che se fosse accertato che i neutrini viaggiano ad una velocita’ superiore a quella della luce ci sarebbe da riscrivere una parte della fisica e fare i conti con i tachioni. Si tratta sicuramente di una notizia rivoluzionaria ed esaltante ma bisogna essere cauti ed essere certi che non ci siano stati errori nella misura o spiegazioni alternative. Se si dimostrasse vera sarebbe esaltante e rivoluzionaria. La cosa migliore e’ terminare questo breve resoconto con le parole dei fisici del progetto OPERA ( da me opportunamente riassunte):

Nonostante il profondo significato dei risultati ottenuti, il potenziale impatto che loro possono avere sulla fisica e’ cosi grande che deve spingere la comunita’ scientifica a continuare lo studio della velocita’ dei neutrini per cercare di capire se ci possono essere degli effetti sconosciuti e sistematici che possono spiegare l’anomalia osservata. Deliberatamente non tentiamo alcuna interpretazione teorica o fenomenologica dei risultati ottenuti.

Approfondimenti

T. Adam et al., Measurement of the neutrino velocity with the OPERA detector in the CNGS beam: paper su ArXiv
Minos collaboration, P. Adamson et al., Phys. Rev. D76 (2007) 072005
Presentazione dei risultati al cern di Ginevra: streaming qui
Numeri complessi: http://it.wikipedia.org/wiki/Numero_complesso
E.Recami: Piu' veloci della luce? Una panoramica sui risultati sperimentali, in Il Nuovo Saggiatore, vol.17(1-2) (2001), pp.21-29.
Recami E. e Fracastoro Decker M.: I Tachioni, in Il Nuovo Saggiatore, vol.2(3) (1986), pp. 20-29.
Recami E., Tachyon Mechanics and Causality; A Systematic Thorough Analysis of the Tachyon Causal Paradoxes, in Foundations of Physics, vol.17 (1987), pp.239-296.
E.Recami: Classical Tachyons and Possible Applications, Rivista del Nuovo Cimento, vol.9, fascicolo monografico n.6 (1986), pp.1-178

La matematica e’ un invenzione o una scoperta dell’uomo?

Uno degli aspetti piu' affascinanti della matematica e' che molto spesso quelli che sembrano sviluppi fini a stessi (matematica pura), inaspettatamente trovano applicazione nel mondo fisico per spiegare i fenomeni naturali. Non a caso Einstein si chiedeva: "Come e' possibile che la matematica, un prodotto del pensiero umano indipendente dall'esperienza, riesca a spiegare cosi egregiamente la realta' fisica?".  Allo stesso modo lo scienziato premio nobel per la fisica, Eugene Wigner's, nel 1960 pubblico' un articolo dal titolo " L'irragionevole efficacia della matematica nelle scienze naturali" dove citava diversi esempi: 

1. Le leggi di Newton. Wigner noto' che le leggi di Newton del moto coinvolgono nozioni astratte come per esempio la derivata seconda, semplice come concetto solo per i matematici e contrario al senso comune. Inoltre queste leggi sviluppate inizialmente per corpi in caduta libera sulla superficie terrestre, furono utilizzate negli anni successivi per spiegare tanti altri fenomeni come i moti planetari, sulla base di osservazioni molto esigue.
2. La meccanica quantistica. Il fisico Max Born per primo noto' che alcune regole di calcolo sviluppate ad hoc da Heisenberg erano formalmente identiche a quelle sulle matrici stabilite molti anni prima dai matematici. Piu' tardi questo formalismo matriciale fu applicato a situazioni, quali l'analisi degli atomi di idrogeno e di elio, e quindi ben oltre lo scopo della stima di Heinseberg, e ancora una volta i risultati furono accurati oltre ogni ragionevole aspettativa.
3. L'elettrodinamica quantistica (QED). Wigner noto' che questa teoria puramente matematica era in accordo perfetto con gli esperimenti con una precisione migliore di una parte su mille. In effetti egli fu molto modesto. Una recente applicazione della teoria QED per trovare il momento magnetico dell'elettrone ha ottenuto un valore di 1.001159652201 (piu' o meno 30 nelle ultime due cifre), confrontato a 1.001159652188 (piu' o meno 4 nelle ultime due cifre) e quindi con una precisione migliore di una parte su un miliardo. E' possibile mai che questa sia solo mera coincidenza?

Wigner chiuse il suo articolo affermando che:

« Il miracolo dell'appropriatezza del linguaggio della matematica per la formulazione delle leggi della fisica è un dono meraviglioso che noi non comprendiamo né meritiamo. Dovremmo esserne grati e sperare che esso rimarrà valido nelle ricerche future e che si estenderà, nel bene o nel male, a nostro piacimento, alle più ampie branche del sapere. »

  

"Una nuova prospettiva e' stata formulata di recente dall'astrofisico Mario Livio. In un articolo apparso questo mese sulla rivista americana Scientific American, egli ha cercato di dare una risposta alle due questioni: "la matematica e' un'invenzione o una scoperta?" e "cosa rende la matematica cosi potente da un punto di vista predittivo ed esplicativo?".

Livio e' convinto che la risposta alla prima questione sia ovvia: la matematica e' una fusione intricata di invenzioni e scoperte. La seconda questione e' piu' complessa. Sebbene non ci sia dubbio che la selezione degli argomenti su cui lavorare scelti dai matematici siano stati fondamentali da un punto di vista dell'efficacia della matematica, questi principi matematici non avrebbero potuto funzionare senza verita' universali da scoprire.
Ci sono due facce per "l'irragionevole efficacia" della matematica: una e' quella che Livio chiama attiva e un'altra quella passiva. La faccia attiva si riferisce a quelle situazioni in cui gli scienziati cercano di fare luce nei labirinti dei fenomeni naturali usando la matematica come torcia elettrica. In altre parole, di sicuro alcune leggi della natura sono formulate in termini matematici. Le entita' matematiche, funzioni, equazioni usate in queste leggi vengono sviluppate ad hoc per queste specifiche applicazioni. Newton, per esempio, sviluppo' la branca della matematica chiamata calcolo infinitesimale perche' aveva bisogno di essa per le sue equazioni del moto. Allo stesso modo, oggi i teorici delle stringhe stanno sviluppando tutta una nuova matematica per le loro necessita'. L'efficacia passiva d'altro canto, si riferisce ai casi in cui delle teorie matematiche astratte sviluppate indipendentemente da eventuali applicazioni finali, solo dopo decenni o addirittura centinaia di anni sono state scoperte avere un ruolo fondamentale nella spiegazioni di fenomeni fisici. C'e' una continua interazione tra l'efficacia passiva ed attiva. Mostriamo un esempio.

 I nodi sono diventati un soggetto di investigazione scientifica serio solo quando nel 1860 Lord Kelvin propose un modello di atomo fatto da tubi annodati di etere. Allo scopo di sviluppare qualche cosa di simile alla nostra tavola periodica degli elementi, lord Kelvin dovette classificare i vari tipi di nodi, cioe' trovare quanti tipi differenti di nodi esistono. Questa necessita' fece nascere un grande interesse per la matematica dei nodi, oggi conosciuta come teoria dei nodi. Questo e' un perfetto esempio di quello che Livio chiama l'aspetto attivo dell'efficacia della matematica. I fisici e matematici del tempo, infatti, credendo che i nodi fossero un possibile modello degli atomi si lanciarono in un entusiastico studio della teoria dei nodi.

Un nodo matematico e' molto simile a quello che conosciamo noi per esempio, quando annodiamo uno spago. L'unica differenza e' che i nodi matematici hanno le estremita' congiunte. Uno degli obiettivi principali della teoria dei nodi e' stato sempre quello di voler identificare le proprieta' che distinguono i vari tipi di nodi, cioe' trovare quello che i matematici chiamano i nodi invarianti. Un nodo invariante agisce come un'impronta digitale del nodo; esso non cambia quando sottoposto a deformazione superficiale (vedi immagine seguente).

Solo dopo circa 100 anni dalla nascita della teoria dei nodi, il matematico Vaughan Jones ha trovato un rapporto inaspettato tra i nodi e un altro ramo della matematica astratta, noto come algebre di von Neumann. Cio' ha portato alla scoperta di un invariante denominato polinomio di Jones. Questo polinomio permette di distinguere, per esempio, i nodi e le loro immagini speculari dove invece le teorie precedenti fallivano. In seguito a questa scoperta c'e' stata una sconcertante varieta' di settori in matematica e fisica che hanno mostrato degli impressionanti collegamenti, non ultima la teoria delle stringhe una delle poche teorie che sembra poter conciliare la relativita' generale con la meccanica quantistica. I teorici delle stringhe, Hirosi Ooguri e Cumrun Vafa hanno scoperto che il numero di strutture topologiche che si formano quando interagiscono tra loro molte stringhe e' legato proprio al polinomio di Jones. Inoltre, uno dei fisici delle stringhe piu' noto, Ed Witten, ha dimostrato che il polinomio di Jones offre nuove prospettive nella teoria quantistica dei campi, uno dei settori piu' importanti della fisica moderna. La lezione che emerge da questa breve storia e' notevole. All'inizio e' stata l'efficacia attiva della matematica ad entrare in gioco. I fisici avevano bisogno di un modello per l'atomo, e quando sembro' che i nodi potessero essere uno strumento adatto decollo' una teoria matematica dei nodi. Una volta che Bohr scopri un migliore modello matematico per descrivere l'atomo, i matematici comunque non abbandonarono la teoria dei nodi. Spinti semplicemente dalla loro curiosita', continuarono ad esplorare le proprieta' dei nodi per molti decenni. All'improvviso poi e' arrivata la sorprendente efficacia passiva della matematica. Inaspettatamente, il polinomio di Jones e la teoria dei nodi in generale, si e' rivelato avere delle ampie applicazioni nella teoria delle stringhe. Quello che rende questa storia ancora piu' sorprendente e' il seguente fatto. Quando lord Kelvin inizio' a studiare i nodi lo fece perche' cercava di modellizzare gli atomi, i mattoni fondamentali della materia. Seguendo il cerchio della storia, adesso la teoria dei nodi cerca di dare delle risposte nella teoria delle stringhe, una delle ultime teorie fisiche che tenta di spiegare i costituenti ultimi della materia. Quindi la teoria dei nodi emersa da un tentativo di spiegare la realta' fisica, per anni rimasta intrappolata nel regno astratto della matematica pura e' ritornata di nuovo alla sua origine ancestrale. Tutto questo non e' assolutamente incredibile?   

Livio chiude il suo articolo chiedendosi:

"Perche' esistono delle leggi universali ? O ugualmente: Perche' il nostro universo e' governato da certe simmetrie? Io davvero non conosco le risposte, anche se va notato che forse in un universo senza queste proprieta', la complessita' e la vita non sarebbero mai emerse, e noi non saremmo qui a porci queste domande."  

 

 

Approfondimenti

• Max Jammer, Einstein and Religion, Princeton University Press, 1921.
  
• Mario Livio, "Why Math Works," Scientific American, Aug 2011, pg. 82-83.
  
• Eugene Wigner, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," in Communications in Pure and Applied Mathematics, vol. 13, No. 1 (Feb 1960), John Wiley and Sons, New York.
  
• Felice Russo, L'Universo dei numeri, I numeri dell'universo, Aracne editrice, 2011
  

I numeri primi circolari

Vorrei iniziare questa mia nuova esperienza come “blogger” con un argomento di teoria dei numeri riguardante i numeri primi, gli atomi fondamentali dei numeri naturali. Ricordo che un numero e’ primo se e’ divisibile per 1 e per se stesso. L’uno non e’ considerato un numero primo.

Siete pronti?  Si parte!

Consideriamo un numero in base decimale con k cifre:

e supponiamo che esista un operatore matematico R che fa ruotare le cifre di questo numero in senso orario, cioè:

Con k cifre il numero massimo di differenti numeri che si possono generare è uguale a k. Qui di seguito un esempio per un numero con 3 cifre.

123   312   231  123

Osserviamo che se un numero ha la stessa cifra ripetuta più volte esso rimane lo stesso ad ogni applicazione dell’operatore R, cioè il numero è invariante rispetto a R. Un esempio è il numero 111.

Fin qui nulla di eclatante. Le cose si fanno più interessanti se invece di considerare dei numeri qualsiasi  fissiamo la nostra attenzione ai numeri primi.

Diciamo che un numero primo è circolare se rimane primo ad ogni rotazione ciclica delle sue cifre. Se un  numero primo contiene una cifra pari o uguale a 5, ovviamente, non può essere un primo circolare. I numeri primi circolari possono essere composti solo dalle cifre: 1, 3, 7, 9.  Qui di seguito un esempio per il numero primo   9311:

1193, 3119, 9311, 1931

Poiché i 4 numeri ottenuti sono tutti primi possiamo concludere che 9311 è un primo circolare.  Il più piccolo numero primo tra i quattro è chiamato primeval. In questo caso il primeval è il numero 1193. È possibile costruire una sequenza di tutti i numeri primeval, come mostrato di seguito:

2  3  5  7  11  13  17  37  79  113  197  199  337  1193  3779  11939 19937  193939  199933

dove con

è stato indicato un primo  repunit con n cifre. Si chiama repunit, un numero formato da tanti 1. Un repunit con n cifre può  essere rappresentato  con la seguente formula:

 Ritorniamo alla sequenza dei primeval notando che tutti i termini riportati sono gli unici conosciuti fino ad oggi.

Se escludiamo i repunit, una domanda cui oggi nessuno sa dare una risposta è la seguente: il numero di primeval è finito o infinito? È possibile, comunque,  fare delle congetture, cioè delle ipotesi ragionevoli ma che rimarranno tali fino a, quando qualcuno non le dimostrerà.
In un  mio articolo,  pubblicato sulla rivista Spectrum Vol. 32 nel 2000, ho mostrato che il numero di primi circolari con d cifre  può essere calcolato in  modo approssimato con la seguente formula:

Questa relazione converge rapidamente verso zero e quindi è lecito supporre che il numero di primi circolari sia finito. Ma è solo una congettura.

Nella Tabella sottostante è riportata la stima e il numero effettivo di primi circolari con d cifre ad oggi conosciuti.  

Cosa possiamo dire, invece, dei primi repunit?

Gli unici conosciuti ad oggi sono quelli con 2, 19, 23, 317 e 1031 cifre. Altri tre repunit, invece al momento sono solo dei primi probabili in quanto ancora non hanno passato tutti i test di primalità. Questi numeri hanno  49081, 86453, 109297 e 270343 cifre. Immaginate che file di 1. Notare che tutti i repunit primi hanno un numero di cifre che è anche esso un numero primo.

Anche per i primi repunit, come per i circolari primi, è plausibile pensare che il loro numero sia finito. Ma è proprio cosi?

Al momento nessuno lo sa. Ma sono molti quelli che credono che essi siano infiniti. Per capire il perchè basta dare un’occhiata  al grafico qui sotto dove sull'asse delle x viene riportato il rango dei repunit e sull'asse delle y il logaritmo del logaritmo del repunit.

Qualcuno vuole cimentarsi nella ricerca di numeri primi circolari o dei repunit? Se si fatemi sapere cosa incontrerete nella grande prateria dei numeri primi.