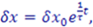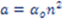E’ molto probabile che la maggior parte del lettori conoscano l’indice di massa corporea. Chi infatti, non si e’ trovato almeno una volta nella sua vita a dover fare una dieta per recuperare il peso forma? La sua definizione risale al 1830 grazie allo scienziato A. Quetelet che derivo’ questa formula per stimare la “grassezza” del corpo umano. La formula e’ molto semplice: si tratta del rapporto tra il peso in chilogrammi e il quadrato dell’altezza espressa in metri.
Facciamo un esempio. Se il mio peso e’ di 100Kg e l’altezza di 1,80 metri allora il mio indice di massa corporea tipicamente espresso con l’acronimo BMI risulta essere di 30,86 Kg/m2.
Questo parametro da molti e’ considerato un buon indice per giudicare se una persona ha o no problemi di peso (obesita’ o anoressia). Nel grafico sottostante e’ riportato il peso in Kg sull’asse delle ordinate e l’altezza in metri su quello delle ascisse. I diversi colori indicano il grado di “grassezza” e di “magrezza” di una persona.
Va precisato, tuttavia, che è errato utilizzare solo altezza e peso come dati sufficienti per calcolare il peso ideale, trascurando caratteristiche morfologiche di base, quali larghezza delle spalle, larghezza ossea del bacino, circonferenza cranica, rapporto tra lunghezza delle gambe e lunghezza del tronco, corporatura di tipo tendenzialmente muscoloso o flaccido e tanti altri fattori, o fattori ancora più basilari come il sesso dell'individuo.Secondo il professore Nick Trefethen, un matematico dell’Universita’ di Oxford, la formula stessa dell’indice di massa corporea contiene un errore come egli ha annunciato in una lettera inviata al The Economist (link):
“Se tutte e tre le dimensioni di un umano scalassero allo stesso modo durante la sua crescita, allora una formula del tipo peso/altezza3 andrebbe bene. Ma non e’ cosi. Comunque peso/altezza2, l’attuale formula del BMI, non e’ realistica.
Un’approssimazione migliore della realta’ e’ data da peso/altezza2.5 che e’ la formula che io propongo. Se si riporta il peso delle persone verso la loro altezza il risultato e’ qualche cosa di molto vicino alla mia formula. “
L’attuale BMI, sempre secondo il professore Trefethen comporta confusione e risultati fuorvianti. A causa del termine altezza2, la formula divide il peso per un numero troppo grande per persone basse e troppo piccolo per perone alte. In questo modo le persone basse sono indotte a pensare che loro sono piu’ magri di quanto non siano nella realta’ e le persone alte di essere piu’ grasse di quello che sono.
La formula proposta e’:
New BMI=(1.3M)/(H2.5)
dove M e’ la massa in Kg e H e’ l’altezza in metri.
Come il professore spiega essendo il nostro mondo tridimensionale, la presenza dell’esponente 2 e’ anomala. Ci si aspetterebbe infatti un esponente pari a 3. Ma le cose non stanno cosi in quanto le misure di altezza e peso delle persone indicano un’esponente pari a 2.5 anche se egli non riporta alcun dato a supporto. Il pre fattore 1.3 deriva dall’assunzione che una persona di peso medio (non riportato) e altezza pari a 1.69 metri debba avere lo stesso BMI della formula di Quetelet. Ovviamente anche in questo caso la scelta e’ del tutto arbitraria. Nel grafico sottostante e’ riportato l’indice BMI verso l’altezza in metri per una persona di peso pari a 75Kg. Da notare come la nuova formula dia un indice BMI sempre piu’ elevato di quello di Quetelet man mano che l’altezza diminuisce. A parita’ di peso piu’ una persona e’ bassa e piu’ e’ alto il suo indice di massa corporea. La differenza tra i due indici invece e’ meno significativa per le persone piu’ alte dove il nuovo indice e’ solo un 10% piu’ basso (non apprezzabile nel grafico).
Al di la delle differenze che la nuova formula introduce come e’ possibile giustificare un andamento del BMI con un altezza elevata ad un esponente pari a 2.5?L’indice BMI lo possiamo vedere come il rapporto tra la massa e il volume del corpo umano. Supponiamo di poter assimilare quest’ultimo ad un cilindro di altezza h ed area di base pari a pi(d/2)2 dove d e’ il diametro del cerchio che circoscrive le spalle e pi e’ la costante pi greco. Il volume di questo cilindro e’ dato da:
V=pi*h(d/2)2 (*)
Se assumiamo che d~h2/3 allora il rapporto M/V e’:
M/V=(4M/pi)*h7/3=(1.27M)/h2.33
che e’ molto prossimo alla formula presentata dal professore Trefethen.
Ma l’assunzione che la larghezza delle spalle scali con l’altezza elevata a 2/3 e’ corretta? L’unico data base con dati di statura e diametro del corpo umano che sono riuscito a trovare sul web e’ un vecchio articolo del Dr. Magnanini del 1900. Utilizzando la tabella N. 3 in esso riportata ho ottenuto una relazione molto prossima a quella che ho ipotizzato sia per il diametro verso l’altezza che per il volume verso l’altezza. Ci si rende conto che questi dati sono molto vecchi e che andrebbero confermati con valori piu’ recenti. Ma al momento e’ il meglio che ho potuto fare.
L’assunzione che nella formula del BMI vada considerato un esponente 2.5 (o meglio 2.33?) anziche’ 2 significa assumere che il volume del corpo umano scala come un frattale di dimensione pari a ~2.5. L’esponente 2.5 indica che il corpo umano non e’ assimilabile ne ad un piano ne ad un cubo, ma sta nel mezzo. Questo non ci deve sorprendere in quanto sappiamo che tutti noi siamo dei frattali. I nostri polmoni, il nostro sistema circolatorio, il nostro cervello sono tutte strutture frattali. La geometria frattale permette di avere figure geometriche con area finita e perimetro infinito, volume finito e superficie infinita. La maggior parte degli oggetti naturali sono composti da molti differenti tipi di frattali intrecciati uno nell’altro, ed ognuno con una sua dimensione Il tipo di relazione ipotizzata tra il volume e l’altezza (o equivalentemente tra diametro ed altezza) e’ molto comune in biologia e’ prende il nome di relazione allometrica. A differenza delle relazioni isomeriche dove la variabile y e una x sono legate tra loro in modo lineare (cioe’ y=kx) quelle allometriche mostrano una dipendenza non lineare (y=bxa con a≠1). Per capire meglio il concetto basta dare un occhiata alle due immagini sottostanti. Assimilando l’albero ad un triangolo in caso di relazione isomerica significa che col trascorrere del tempo i tre lati aumenteranno tutti dello stesso fattore, mentre questo non e’ vero nel caso delle relazioni allometriche.
Relazione isomerica
Relazione allometrica
Le relazioni allometriche del tipo potenza sono una classe di relazioni molto importanti in quanto hanno la proprieta’ di non avere una lunghezza di scala particolare (infatti si chiamano scale-free) e valgono per diversi ordini di grandezza. Oggetti invarianti per scala hanno lo stesso aspetto quando vengono riscalati in modo opportuno (...di nuovo i frattali).Ecco perche’ le relazioni allometriche sono delle leggi di potenza e non un esponenziale. Infatti nel caso che
Y=bxa
Se riscaliamo la x in rx si ha
Y=b(rx)a=braxa=b’xa
che ha la stessa forma funzionale iniziale. Nel caso invece di una legge esponenziale si ha:
y=be-ax
e riscalando la x in rx si ha:
y=be-arx
che come si vede non e’ la stessa forma iniziale in quanto quest’ultima ha una scala caratteristica data da 1/ar contro la scala 1/a di quella iniziale. Una relazione allometrica molto famosa e’ quella che va sotto il nome di legge di Gutenberg-Richter che lega l’intensita’ dei terremoti espressa in magnitudo verso la frequenza con con cui i terremoti si presentano. Essendo scale-free la relazione vale per i terremoti di piccola magnitudo fino ad arrivare a quelli catastrofici. Essa ci dice che ci sono tanti terremoti di piccola intensita’ e raramente quelli catastrofici.