Sono tanti quelli che hanno avuto la possibilità di ammirare la grandiosità delle piramidi di Giza. Si tratta di opere straordinarie su cui ancora molto si discute. Non si sa ancora con certezza, se all’interno le pareti erano ricoperte di pitture e geroglifici come quasi tutte le altre tombe egizie. Se effettivamente fossero strutture legate ad oggetti stellari (vedi per esempio la teoria di Bouval secondo la quale le tre piramidi altro non sono che la rappresentazione sulla terra delle stelle della cintura della costellazione di Orione) o se invece fossero delle semplici tombe.
In questo capitolo, anche noi, ci occuperemo di piramidi, ma di piramidi matematiche i cui mattoni sono le pietre infrangibili della matematica: i numeri primi.
Ma non tutti i primi vanno bene. Per generare la simmetria delle piramidi rispetto all’asse centrale, bisogna considerare solo i primi palindromi. Ricordiamo che i numeri palindromi sono quei numeri che si leggono allo stesso modo da sinistra a destra e viceversa. Partendo col numero primo 2, per esempio, è possibile costruire due piramidi di altezza 5. Diversamente dagli antichi, noi costruiamo le nostre piramidi dall’alto verso il basso.
Ogni gradino è un numero primo palindromo con il precedente gradino che costituisce le cifre centrali. Queste due piramidi sono le più alte che si possono costruire partendo con il numero 2. Le piramidi più alte che si possono costruire partendo con i numeri primi di una sola cifra sono raffigurate di seguito.
Ma è possibile costruire piramidi sempre più alte?
Se invece di considerare come punto di partenza numeri primi ad una cifra, iniziamo le piramidi con numeri primi palindromi con più cifre è possibile costruirne di più alte? E l’altezza di queste piramidi è sempre finita? Abbiamo visto che partendo con un numero primo ad una cifra e aggiungendo ad ogni lato una nuova cifra, l’altezza massima che si riesce ad ottenere è 5. Questo perché dovendo essere ogni gradino un numero primo abbiamo solo 4 possibili scelte per le cifre da aggiungere su ogni lato: 1, 3, 7, 9.
Partendo con numeri primi più grandi probabilmente non aiuta molto di più. Ma ce ne sono così tanti con cui partire che si può avere fortuna. Qui un esempio di tronco di piramide di altezza 9, che ho trovato nel 2000 e pubblicato in internet sul sito dell’Enciclopedia on-line delle sequenze di numeri interi con codice identificativo A046210.
7159123219517
371591232195173
33715912321951733
7337159123219517337
973371591232195173379
39733715912321951733793
3397337159123219517337933
933973371591232195173379339
39339733715912321951733793393
Se invece di aggiungere due cifre, una per ogni lato, consideriamo la possibilità di aggiungerne 4, due per lato, allora partendo con il numero primo 2 è possibile costruire una piramide costituita da ben 26 gradini come mostrato di seguito. Proprio una bella struttura.
2
30203
903020309
3790302030973
98379030203097389
969837903020309738969
9996983790302030973896999
72999698379030203097389699927
997299969837903020309738969992799
9099729996983790302030973896999279909
94909972999698379030203097389699927990949
779490997299969837903020309738969992799094977
7977949099729996983790302030973896999279909497797
17797794909972999698379030203097389699927990949779771
751779779490997299969837903020309738969992799094977977157
7375177977949099729996983790302030973896999279909497797715737
72737517797794909972999698379030203097389699927990949779771573727
987273751779779490997299969837903020309738969992799094977977157372789
3098727375177977949099729996983790302030973896999279909497797715737278903
70309872737517797794909972999698379030203097389699927990949779771573727890307
397030987273751779779490997299969837903020309738969992799094977977157372789030793
3539703098727375177977949099729996983790302030973896999279909497797715737278903079353
36353970309872737517797794909972999698379030203097389699927990949779771573727890307935363
333635397030987273751779779490997299969837903020309738969992799094977977157372789030793536333
3433363539703098727375177977949099729996983790302030973896999279909497797715737278903079353633343
99343336353970309872737517797794909972999698379030203097389699927990949779771573727890307935363334399
La stessa cosa si può fare usando come seme di partenza gli altri numeri primi di una sola cifra. C’è una piramide di altezza 29 per entrambi i numeri di partenza 5 e 7, mentre per il numero primo 3 la massima altezza è 28.
Sicuramente aumentando la dimensione della stringa di numeri da aggiungere ai due lati porterà a piramidi con altezze sempre maggiori. Ma di quanto? Quante piramidi è possibile costruire?
Indichiamo con l(n) il numero di cifre del numero n. Sia f(n,h,d) il numero di piramidi con altezza h, con numero primo iniziale n e con d cifre aggiunte ad ogni passo.
Per esempio, f(2,1,d)=1 in quanto c’è una sola piramide con numero iniziale 2 e altezza 1.
Al contrario f(101,2,2)=4 in quanto ci sono 4 piramidi con numero iniziale 101, altezza 2 e passo 2.
È possibile stimare la funzione f(n,h,d) e quindi calcolare la massima altezza ottenibile?
La risposta è si.
In base al teorema dei numeri primi, il numero di primi tra 2 e x è dato in modo approssimato da x/ln(x). Un’interpretazione di questo teorema è che la probabilità che un numero intero scelto a caso sia primo è dato da 1/ln(x). Quando costruiamo la piramide di numeri primi palindromi spostandoci da un gradino a quello successivo, ci sono 10*d interi da provare e quindi:
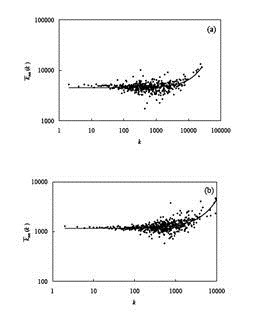
Nella figura di seguito è riportato l’andamento della curva approssimata per il caso n=2 e d=2.
Grafico della funzione f(2,h,2)/f(2,h-1,2). Notare l’ottimo accordo tra i dati reali
e quelli stimati. La coincidenza tra i dati e la curva approssimata è molto buona.
Osservare che man mano che h cresce il numero delle piramidi comincia a decrescere rapidamente e tende verso zero.
Per questo motivo, due studiosi di numeri primi, G.L. Honaker e Chris Caldwell, hanno congetturato che:
Congettura: Tutte le piramidi prime palindrome con un fissato passo d, hanno un’altezza finita.
Essi hanno inoltre trovato una formula per f(n,h,d) data da:
Osservare che per d=3 e n=2 questa relazione predice che ci dovrebbero essere circa 1030 possibili piramidi. Questo fa capire che voler cercare le piramidi più alte con un programma per computer è impensabile. Considerando, comunque, un numero limitato di piramidi (un massimo di 160), Honaker e Caldwell hanno trovato un altezza massima di 94, 101, 102, e 100 per i numeri primi di partenza 2, 3, 5,e 7 rispettivamente. Se fissiamo il passo d, questo limita le piramidi ad avere un’altezza finita. E se invece permettiamo a d di prendere qualsiasi valore? Argomenti analoghi a quelli riportati precedentemente suggeriscono che per qualsiasi numero primo palindromo di partenza si dovrebbe essere capaci di costruire piramidi tanto alte quanto si vuole. Chiaramente l’altezza h delle piramidi in media è proporzionale allo step d. C’è un caso particolare molto interessante. Supponiamo che per ogni gradino della piramide, il numero palindromo da utilizzare, sia il più piccolo possibile indipendentemente da d. In questo caso partendo da 2 la piramide inizialmente dovrebbe essere la seguente:
2
727
37273
333727333
93337273339
309333727333903
1830933372733390381
92183093337273339038129
3921830933372733390381293
1333921830933372733390381293331
18133392183093337273339038129333181
Questa piramide può essere considerata come una sequenza dove ogni termine è rappresentato da un gradino. Cioè: a1=2, a2=727, a3=37273 ........
Questa sequenza può anche essere condensata scrivendo a1 seguito dalle cifre che sono aggiunte sulla sinistra ad ogni stadio della piramide.
2, 7, 3, 33, 9, 30, 18, 92, 3, 133, 18, 117, 17, 15, 346, 93, 33, 180, 120, 194, 126, 336, 331, 330, 95, 12, 118, 369, 39, 32, 165, 313, 165, 134, 13, 149, 195, 145, 158, 720, 18, 396, 193, 102, 737, 964, 722, 156, 106, 395, 945, 303, 310, 113, 150, 303, 715, 123
Un’altra sequenza di numeri primi palindromi può essere generata cercando di dare una risposta ad una questione che l’autore ha pubblicato su internet nel 2000 (sequenza A046210) e che recita:
Qual è il più piccolo numero primo palindromo che genera una piramide di altezza massima n?
La sequenza considerando d=1, inizia con:
11, 131, 2, 929, 10301, 16361, 10281118201, 35605550653, 7159123219517…
11 è il più piccolo numero primo che genera una piramide di altezza 1.
Infatti, tutti i numeri che si possono formare con le cifre 2, 3, 7, 9 non sono primi.
Il numero primo successivo 131, è il più piccolo numero primo che forma una piramide di altezza 2 e cosi via.
Come continua questa sequenza? Ad oggi nessuno lo sa, anche se nuove scoperte possono essere dietro l’angolo.