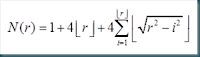Numeri geometrici

 

Possono i numeri avere una forma geometrica?

Anche se e’ chiaro di no, alcuni di essi possono essere rappresentati da punti disposti come figure geometriche regolari. Questi numeri vengono chiamati numeri figurati o numeri poligonali.
I numeri figurati più conosciuti sono i numeri quadrati, cioè i numeri 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121,…….
Essi si chiamano così perché possono essere disposti all’interno di quadrati come quelli riportati sotto.

Gli angoli rossi sono quelli che gli antichi Greci chiamavano “gnomon”. Ogni quadrato e’ formato dal quadrato precedente indicato in blu più lo gnomon. I numeri appartenenti allo gnomon dei numeri quadrati sono: 1, 3, 5, 7, 9, 11,…. Praticamente i numeri dispari.

Da qui discende facilmente che l'ennesimo numero quadrato e’ dato dalla somma del quadrato precedente piu' i numeri dispari consecutivi. Allo stesso modo e’ possibile trasformare in termini matematici quello che abbiamo visto con la rappresentazione geometrica, cioè che e’ vera la seguente formula ricorsiva per i numeri quadrati Q:

Q_k+1=Q_k+2k+1

dove k=0, 1, 2, 3, 4…. e Q₀=0

Il numero di rappresentazioni di un numero n tramite k quadrati, distinguendo il segno e l’ordine, viene indicato con r_k(n); si tratta di una funzione di n chiamata la funzione della somma dei quadrati. Per esempio, consideriamo il numero di modi in cui e’ possibile rappresentare il numero 5 come somma di 2 quadrati:

e quindi r₂(5)=8. Allo stesso modo il numero 4 puo’ essere scritto come somma di tre quadrati come segue:

e quindi r₂(4)=6.

Diversi grandi matematici hanno contribuito a determinare un’espressione analitica di questa funzione. Jacobi ci riusci’ nel 1829 per k=2,4,6, e 8. La soluzione per k=10 e 12, invece, fu trovata da Liouville e in seguito da Eisenstein. Glaisher nel 1907, riusci a sviluppare una tabella di  r_2s(n) per 2s fino a 18. Il grande Ramanujan, estese il risultato di Glaisher fino a 2s=24.

La funzione  r₂(n) a volte indicata come r(n) e’ intimamente connessa al problema del cerchio di Gauss.

Questo problema consiste nel contare, per un cerchio di raggio r, il numero dei punti del reticolo N(r), all’interno dei confini del cerchio (confine incluso) con centro nell’origine (vedi figura 1).

 

Figura 1: Problema del cerchio di Gauss.

L’esatta soluzione di questo problema e’ data dalla formula:

dove la funzione

indica la parte intera del numero n. I primi valori di N(r) per r=0,1,2,3…. sono 1, 5, 13, 29, 49, 81, 113, 149…….

La serie N(r) e’ legata alla funzione della somma di due quadrati r(n) in quanto si puo’ dimostrare che:

In figura 2, viene riportata la rappresentazione della funzione N(r)/r²  in funzione di r. Osservare l’andamento asintotico della funzione dopo aver attraversato una zona per bassi valori di r con grosse oscillazioni.

 

Figura 2: Andamento del rapporto N(r) e il quadrato di r

I numeri 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, ... sono invece i cosiddetti numeri triangolari in quanto possono essere rappresentati tramite triangoli regolari.

Se con T_k indichiamo il k-esimo numero triangolare si può verificare che vale la seguente relazione:

con T₀=0.

Questa relazione ricorsiva può essere espansa per dimostrare che il k-esimo numero triangolare altro non e’ che la somma di tutti numeri da 1 a k.

Poiché la somma dei primi k numeri e’ data da k(k+1)/2 possiamo scrivere che:

Osservare che a partire dai numeri triangolari si possono ottenere i numeri quadrati. E’ facile, infatti, dimostrare che:

Schematicamente questa relazione può essere rappresentata nel seguente modo:

Qui l’n-1_esimo numero triangolare e’ rappresentato dai triangoli bianchi, l’n_simo numero triangolare dal numero di triangoli neri mentre il numero totale dei triangoli e’ l’ennesimo numero quadrato.

Un'altra relazione dimostrata da Conway e Guy nel 1996, lega i numeri triangolari a quelli quadrati.

Si può verificare che essa e’ vera osservando che e’ sempre possibile dividere un quadrato in 8 triangoli a parte un tassello.

Nel 1638, Fermat propose che ogni numero intero positivo, e’ la somma di almeno tre numeri triangolari, quattro numeri quadrati, cinque numeri pentagonali e cosi via.

Egli riportò di avere una dimostrazione, anche se essa non e’ mai stata trovata.

In seguito Gauss provò che il caso dei numeri triangolari era vero e annoto’ l’evento sul suo diario (10 Luglio 1796) con la scritta ormai famosa:
 

Il caso dei numeri quadrati fu dimostrato da Jacobi e Lagrange nel 1772, mentre l’intero teorema e’ stato dimostrato solo nel 1813 da Cauchy.

Allo stesso modo dei numeri triangolari e numeri quadrati e’ possibile costruire numeri pentagonali, esagonali, ettagonali ….. In generale possiamo parlare di numeri poligonali. Questi numeri sono caratterizzati da due parametri: il numero E dei vertici e il numero k del rango (il primo, secondo, terzo etc). Il minimo valore per questi due parametri e’ 3 ed 1 rispettivamente.

Con G(E,k) indichiamo il numero poligonale con E vertici e allo stadio k.

I numeri:

G(3,k) rappresentano i numeri triangolari

G(4,k) i numeri quadrati

G(5,k) i numeri pentagonali

G(6,k) i numeri esagonali

G(7,k) i numeri ettagonali

G(8,k) i numeri ottagonali

e cosi via. I numeri poligonali sono numeri i cui punti che li rappresentano possono essere disposti all’interno di poligoni regolari. Allo stadio k=1 ogni numero poligonale e’ costituito da un solo punto, cioè G(E,1)=1. Per k maggiore o uguale a 2   il numero poligonale appartenente alla famiglia G(E,k) evolve da quello precedente G(E,k-1) mettendo insieme una “catena” aperta di nuovi punti ai k-2 lati del vecchio pattern cosicché i vertici andranno a formare un nuovo poligono con esattamente k punti su ognuno dei suoi lati.

Nei seguenti esempi in blu vengono riportati i precedenti pattern e in rosso le catene aperte dei nuovi punti.

Esempio di numeri pentagonali.

Esempio di numeri esagonali.

Da queste figure si può facilmente dimostrare che:

La persistenza dei numeri e altre amenita’ dall’enciclopedia OEIS

   

Sicuramente sara’ capitato a molti di voi che amano la matematica di imbattersi almeno una volta nel sito del Dr. Neil Sloane dei Laboratori AT&T del New Jersey in America. Si tratta del piu’ grande data base di numeri esistente al mondo. Si chiama “On line Encyclopedia of Integer Sequences” con circa 200.000 sequenze numeriche. Questo l’indirizzo web. Una sequenza e’ una lista di numeri, eventualmente infinita, che puo’ essere calcolata utilizzando delle semplici regole.

La sequenza piu’ famosa e’ sicuramente quella di Fibonacci dove ogni termine e’ dato dalla somma dei due termini precedenti: 1, 1, 2, 3, 5, 8, 13, 21, 34,.....

Il Dr. Sloane ha lavorato a questa enciclopedia per circa 40 anni ed oggi e’ consultata gratuitamente tramite il web da diversi scienziati nel mondo. Gli astronomi, per esempio, che cercano possibili vite extra-terresti analizzando i segnali radio che arrivano dall’Universo, la consultano per capire se si tratta di una sequenza casuale o no.

Essa aiuta anche le compagnie di telefoni mobili quando cercano di eliminare le interferenza tra diverse chiamate. In effetti, quando facciamo una chiamata, ci viene assegnata una certa frequenza che non deve interferire con quelle di altre persone.

Frequenze basate su sequenze di numeri che non si ripetono mai, individuabili grazie al data base di Sloane, garantiscono al cliente l’assenza di disturbi di interferenza.

Un altro aiuto viene dato agli esperti di crittografia che utilizzano la fattorizzazione dei numeri primi per trasmettere messaggi segreti.

All’interno di questo grande contenitore online, si possono trovare successioni di numeri di diverso tipo. Da quelle semplici a quelle difficili da calcolare, da quelle ordinate a quelle disordinate, da quelle basate sul calcolo combinatorio  a quelle ricreazionali. Anche io negli anni passati ho dato un piccolo contributo a questa enciclopedia  inserendo alcune mie sequenze che potete consultare  a questo link.

Neil Sloane ha una lista di quelle che lui ritiene le sue favorite. Vediamo quali sono.

La prima e’ la sequenza di Recaman, che inizia come la sequenza di Fibonacci per poi diventare significativamente diversa. Questa sequenza e’ molto difficile da analizzare in quanto non mostra alcuna regolarita’, non aumenta, non diminuisce e ne’ oscilla in modo regolare.

Se provassimo a graficare i numeri di Fibonacci, questi crescerebbero in modo prevedibile, con una velocita’ ben determinata. La sequenza di Recaman, invece, barcolla come un ubriaco, andando su e giu’ in modo del tutto casuale. Il suo grafico assomiglia allo scarabocchio di un bambino.

La regola alla base e’ molto semplice:

Supponendo di partire con 1, si ottiene facilmente:

1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, .......

Nel database di Sloane, in genere, le sequenze che dipendono dalla scelta della base non vengono mantenute anche se ci sono delle eccezioni. Partiamo, per esempio, con un numero n; se esso e’ palindromo (cioe’ se si legge allo stesso modo da sinistra a destra e viceversa, come 121, 25652...) ci fermiamo; altrimenti aggiungiamo il numero n a se stesso con le cifre al contrario. Ripetiamo questa operazione fino a quando non raggiungiamo un numero palindromo, oppure assegniamo -1 se non lo raggiungeremo mai. Partendo con 19, otteniamo:

19 –> 19+91=110 –>110+011=121

che e’ un palindromo, e quindi ci fermiamo e il diciannovesimo termine della sequenza sara’ 121. La sequenza inizia con:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11, 33, 44, 55, 66, 77, 88, 99, 121, 22, 33, 22, 55, 66, 77, . . . .

E se partiamo col numero 196 cosa succede?. In questo caso otteniamo:

196, 887, 1675, 7436, 13783, 52514, 94039, 187088, 1067869, 10755470, 18211171, . . . .

che sembra non raggiungere mai un numero palindromo. Sarebbe interessante avere una dimostrazione di cio’, ma al momento non esiste. Questo e’ uno di quei problemi che sembrano troppo difficili da risolvere per la matematica del XXI secolo.

Un’altra sequenza molto amata da Sloane, e’ quella chiamata “Powertrains” . In questo caso ogni termine della sequenza e’ legato al numero di passaggi necessari per arrivare ad un numero ad una sola cifra partendo da un numero qualsiasi n e moltiplicando tra loro le sue cifre. Partendo con 679, per esempio, sono necessari 5 passaggi per arrivare a 6:

679 –> 378 –> 168 –> 48 –> 32 –>6

Il numero di passaggi e’ chiamato la persistenza del numero; nel caso di 679 la persistenza e’ uguale a 5. I piu’ piccoli numeri naturali con persistenza 1,2,3,4,.... sono dati dalla sequenza:

10, 25, 39, 77, 679, 6788, 68889, 2677889, 26888999, 3778888999, 277777788888899

Sloane, in un articolo del 1973 ha congetturato che questa sequenza e’ finita e fino ad oggi non e’ stato trovato nessun numero naturale con persistenza maggiore di 11.

Tutti sono invitati alla ricerca. Qualcuno dei lettori potrebbe scontrarsi con un numero n con persistenza maggiore di 11 ed entrare nel guinness dei primati della matematica.

Nel 2007, John Conway, l’autore del gioco della Vita, ha proposto una variazione al concetto di persistenza suggerendo di considerare nel caso in cui un numero n ha un’espansione decimale del tipo abcd..., il numero a^bc^d.... che termina in un esponente o una base a seconda che il numero di cifre contenute in n e’ pari o dispari. Si assume che 0⁰ sia uguale ad 1. Questa sequenza comincia con:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 1, 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1, 5, 25, 125, 625, 3125, 15625,…

e il suo grafico e’ mostrato in figura 1.

Figura1: Rappresentazione della sequenza powertrain. Sull’asse y e’ riportato il logaritmo di ogni termine della sequenza piu’ uno.

Se consideriamo la mappa n à Powertrain(n) ci accorgiamo che alcuni punti sono dei punti fissi (o attrattori) come per esempio 2592 essendo 2⁵·3⁴ = 2592 –> 2⁵·9² = 2592. La successione degli attrattori  del Powertrain e’ data da:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 2592, 24547284284866560000000000

e Sloane ha congetturato che non ci sono altri termini. Di sicuro questo e’ vero per 10¹⁰⁰  in quanto e’ stato verificato con una ricerca esaustiva al computer. Ancora una volta regole molto semplici possono dar origine a questioni che potrebbero rimanere senza una risposta per secoli.

Un altra sequenza interessante, che solleva un problema veramente difficile da risolvere e’ la cosiddetta sequenza di Lagarias, definita come:

dove H(n) e’ l’ennesimo numero armonico dato da:

e σ(n) la somma dei divisori di n (per esempio σ(6)=12 in quanto i divisori di 6 sono 1, 2, 3, 6). I primi termini sono riportati nell’ enciclopedia di Sloane e sono:

0, 0, 1, 0, 4, 0, 7, 2, 7, 5, 13, 0, 17, 9, 12, 8, 23, 5, 27, 8, 21, 20, 34, 1, 33, 25, . . .

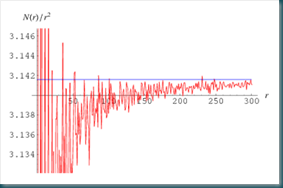
Jeff Lagarias, da cui la sequenza prende il nome, nel 2001 ha dimostrato che se a(n) e’ sempre maggiore o uguale a zero, questo equivale a dire che la famosa ipotesi di Riemann,  e’ vera. In figura 2, viene mostrata un’immagine dell’andamento di questa sequenza per diversi valori di n.

Figura2: Rappresentazione della sequenza di Lagarias.

Continuiamo il nostro viaggio e vediamo quale e’ il nostro prossimo incontro. Si tratta della cosiddetta sequenza EKG. I primi due termini sono 1 e 2, e i termini successivi vengono calcolati considerando il numero positivo piu’ piccolo non presente gia’ nella successione e che ha un fattore comune non banale con il termine precedente. Poiche’ a(2)=2, allora a(3) deve essere pari, ed e’ quindi uguale a 4. a(4) deve avere un fattore comune con 4 e quindi non puo’ che essere uguale a 6. Il piu’ piccolo numero non presente nella sequenza e che ha un fattore in comune con 6 e’ 3, cosicche’ a(5)=3 e cosi’ via. I primi 18 termini di questa successione sono:

1, 2, 4, 6, 3, 9, 12, 8, 10, 5, 15, 18, 14, 7, 21, 24, 16, 20……..

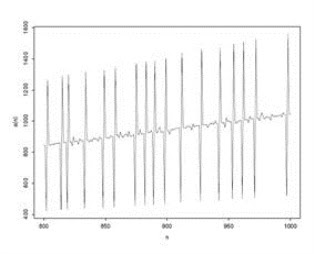
E’ chiaro che se nella sequenza compare un numeri primo p, allora il termine immediatamente precedente o immediatamente successivo sara’ uguale a 2p. Inoltre, Lagarias, Rains e Sloane hanno notato che ogni numero primo p e’ sempre preceduto da 2p e seguito da 3p. Questo e’ stato provato essere vero per i primi 10.000.000 termini della successione. Ma non sono riusciti a trovare una dimostrazione di cio’. Ancora un altro problema aperto su cui potersi cimentare. La sequenza e’ stata chiamata EKG in quanto essa assomiglia ad un elettrocardiogramma quando riportata su grafico come mostrato in figura3.

Figura3: I primi 100 termini della sequenza EKG sopra, e i termini da 800 a 1000 sotto.

Sebbene i primi termini di questa sequenza sembrano ondeggiare, se grafichiamo gli stessi termini della figura 3, senza unire i punti tra di loro con delle linee, otteniamo l’immagine della figura 4.

  Figura4: I primi 1000 termini della sequenza EKG senza unire i punti successivi.

Si puo’ vedere come i valori della sequenza si raggruppano lungo tre linee quasi rette. Questo e’ un comportamento simile a quello dei numeri primi, che inizialmente sembrano imprevedibili, per poi tendere sempre piu’ ad una curva data da ~n·ln(n). C’e’ una precisa congettura per quanto riguarda le tre rette della figura 4, che stabilisce che la maggior parte dei valori della sequenza EKG si stabilizzano intorno alla linea a(n)~n(1+1/(3ln(3)) centrale, ed occasionalmente solo quando a(n)=p, cioe’ in corrispondenza dei numeri primi, vengono prodotti i punti della linea al di sopra a(n)=3p e al di sotto a(n)=p di quella centrale. E’ stato dimostrato che la sequenza ha essenzialmente una crescita lineare nel senso che esistono due costanti c₁ e c₂ tali che c₁n<a(n)<c₂n per tutti i valori di n. Questo e’ tutto quello che si conosce sulla sequenza EKG. Come si intuisce c’e’ ancora tanto lavoro da fare.

E non finisce qui. La prossima sequenza non e’ da meno dell’EKG. Semplice da definire ma difficile da analizzare e tante questioni ancora aperte su cui poter lavorare. Si tratta del problema del quadrato approssimato. Prima di tutto indichiamo col simbolo I(x), il piu’ piccolo intero maggiore o uguale a x. Se partiamo con qualsiasi frazione piu’ grande di 1, come per esempio 8/7, e applichiamo continuamente il prodotto x·I(x) e’ possibile arrivare ad un numero intero.

Poiche’ 8/7=1.142.., I(8/7)=2 e quindi x·I(x)=16/7. Riapplicando lo stesso procedimento alla frazione 16/7 si ottiene 48/7 e poi 48. Per arrivare ad un numero intero sono stati necessari 3 passaggi. La questione che sorge e’: per qualsiasi frazione iniziale, e’ sempre possibile raggiungere un numero intero? Lagarias e Sloane, in un articolo pubblicato sul giornale Experimental Math del 2004, hanno mostrato che quasi tutte le frazioni maggiori di 1 raggiungono un numero intero, e che se il denominatore e’ uguale a 2 allora tutte le frazioni maggiori di 1 raggiungono un numero intero. Comunque una prova completa ancora non esiste. Il problema ha delle similitudini con quello di Collatz che abbiamo analizzato in uno dei post  precedenti, e questo spiega la difficolta’ nel risolverlo.

I numeri coinvolti sono numeri che crescono velocemente. Se partiamo dalla frazione 6/5, per esempio, l’applicazione successiva del prodotto x·I(x), genera la sequenza:

che raggiunge un numero intero con 57735 cifre, dopo 18 passaggi. Se la frazione iniziale ha il denominatore uguale a 2, allora e’ possibile determinare in quanti passaggi si raggiunge un numero intero. Ma se il denominatore e’ gia’ uguale a 3, non sappiamo cosa accade.

Partendo con frazioni della forma (k+1)/k, con k un qualsiasi numero intero, sembra necessario un numero di passaggi veramente lungo primo di approdare ad un numero intero. E’ divertente notare che se k=199, la frazione 200/199 raggiunge un numero intero enorme, approssimativamente uguale a :

cioe’ un numero con circa 10⁴³⁵ cifre. Diversamente da quanto credono la maggior parte delle persone molta della matematica utilizzata per puri scopi teorici, trova poi applicazione nel mondo di tutti i giorni. E’ il caso del classico problema della “dissezione” che e’ stato applicato con successo nel campo delle comunicazioni ottiche.

Dato un poligono con n lati, e’ sempre possibile tagliarlo in un numero finito di pezzi che possono essere arrangiati, senza essere sovrapposti, a formare un quadrato della stessa area.

Ma qual’e’ il minimo numero d(n) di pezzi richiesti?

Per il caso n=3, quello che cerchiamo e’ il minimo numero di pezzi in cui e’ possibile dividere un triangolo equilatero in un quadrato. Al momento il numero minimo conosciuto e’ 4, come mostrato da Dudeney nel 1902 (vedi figura 5). E’ improbabile che si possa fare meglio di cosi ma fino ad oggi nessuno e’ riuscito a provarlo.

Figura5: Un triangolo puo’ essere dissezionato in 4 pezzi che possono poi essere arrangiati a formare un quadrato con la stessa area del triangolo.

Nessuno conosce con certezza i valori di d(n), eccetto chiaramente d(4) che e’ uguale a 1. Si conoscono solo i limiti superiori riportati come sempre nel sito web di Sloane:

4, 1, 6, 5, 7, 5, 9, 7,….

Qualcuno vuole tentare ad abbassare questi limiti?

Esistono altre due sequenze che nascono da due problemi di analisi combinatoria molto interessanti. Il primo si chiama il problema dei “meandri” e il secondo il problema dei “francobolli”. Entrambe queste sequenze di numeri, sono fondamentali, facilmente descrivibili, compaiono in diverse parti della matematica e sono complicate da calcolare.

Nel caso dei francobolli la questione e’ la seguente.

Consideriamo una striscia di francobolli, come mostrato in figura 6. Ci sono n francobolli numerati con 1,2,3,4...n a partire dalla sinistra e ognuno di essi ha una faccia superiore in verde e una faccia inferiore in nero. Tra due francobolli c’e’ una piccola striscia perforata (colore viola nella figura) che facilita la divisione dei francobolli.

Figura6: Striscia di francobolli.

Una tale striscia di francobolli puo’ essere piegata lungo le perforazioni in diversi modi per creare una pila di n francobolli. Assumiamo che le perforazioni siano perfettamente elastiche e quindi possano essere stirate a qualsiasi distanza. Quanti modi diversi esistono per piegare una tale striscia?

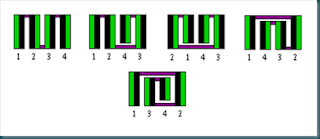
Di seguito viene riportato l’esempio di tutti i possibili piegamenti che si possono ottenere con 4 francobolli.

Alcuni di queste configurazioni sono quasi identiche ad altre, come per esempio, 1234 e 4321. Con lo scopo di rimuovere alcune delle simmetrie, e’ possibile restringere gli orientamenti a quelli in cui il primo francobollo nella sequenza ha il valore piu’ basso dell’ultimo. In questo modo 1234 sara’ permesso mentre 4321 no. Qui sotto viene mostrato il diagramma dei possibili piegamenti dei francobolli con lunghezza 4 rimuovendo le sequenze non permesse. Ci sono esattamente la meta’ degli oggetti del caso precedente.

  Comunque in questo diagramma, ancora esiste un altro tipo di simmetria come quella tra 3214 e 1432. Rimuovendo anche questo tipo di simmetria quello che rimane e’ riportato nell’immagine che segue.

In definitiva la sequenza e’ data da:

1, 1, 2, 5, 14, 38, 120, 353, 1148, 3527, ……

L’altra sequenza, quella dei meandri parte dalla questione: in quanti modi diversi un fiume che scorre da SE a NE, attraversa una strada n volte?

Per n=5 ci sono 8 modi diversi di attraversamento come mostrato nello schema sottostante.

I termini di questa sequenza sono:

1, 1, 2, 3, 8, 14, 42, 81, 262, 538, 1828, ….

Anche se non sono state passate in rassegna tutte le sequenze favorite di Sloane, ci fermiamo qui invitando il lettore interessato a visitare il sito online, a proporre nuove sequenze e a lavorare sui quesiti ancora aperti. Ottima palestra per chi vuole mantenere allenato il proprio cervello.

Considerazioni allometriche sembrano indicare un piccolo errore nella formula del BMI proposta dal professore Trefheten

 

E’ molto probabile che la maggior parte del lettori conoscano l’indice di massa corporea. Chi infatti, non si e’ trovato almeno una volta nella sua vita a dover fare una dieta per recuperare il peso forma? La sua definizione risale al 1830 grazie allo scienziato A. Quetelet che derivo’ questa formula per stimare la “grassezza” del corpo umano. La formula e’ molto semplice: si tratta del rapporto tra il peso in chilogrammi e il quadrato dell’altezza espressa in metri.

Facciamo un esempio. Se il mio peso e’ di 100Kg e l’altezza di 1,80 metri allora il mio indice di massa corporea tipicamente espresso con l’acronimo BMI risulta essere di 30,86 Kg/m2.

Questo parametro da molti e’ considerato un buon indice per giudicare se una persona ha o no problemi di peso (obesita’ o anoressia). Nel grafico sottostante e’ riportato il peso in Kg sull’asse delle ordinate e l’altezza in metri su quello delle ascisse. I diversi colori indicano il grado di “grassezza” e di “magrezza” di una persona.

Va precisato, tuttavia, che è errato utilizzare solo altezza e peso come dati sufficienti per calcolare il peso ideale, trascurando caratteristiche morfologiche di base, quali larghezza delle spalle, larghezza ossea del bacino, circonferenza cranica, rapporto tra lunghezza delle gambe e lunghezza del tronco, corporatura di tipo tendenzialmente muscoloso o flaccido e tanti altri fattori, o fattori ancora più basilari come il sesso dell'individuo.

Secondo il professore Nick Trefethen, un matematico dell’Universita’ di Oxford, la formula stessa dell’indice di massa corporea contiene un errore come egli ha annunciato in una lettera inviata al The Economist (link):

“Se tutte e tre le dimensioni di un umano scalassero allo stesso modo durante la sua crescita, allora una formula del tipo peso/altezza³ andrebbe bene. Ma non e’ cosi. Comunque peso/altezza², l’attuale formula del BMI, non e’ realistica.

Un’approssimazione migliore della realta’ e’ data da peso/altezza^2.5 che e’ la formula che io propongo. Se si riporta il peso delle persone verso la loro altezza il risultato e’ qualche cosa di molto vicino alla mia formula. “

L’attuale BMI, sempre secondo il professore Trefethen comporta confusione e risultati fuorvianti. A causa del termine altezza², la formula divide il peso per un numero troppo grande per persone basse e troppo piccolo per perone alte. In questo modo le persone basse sono indotte a pensare che loro sono piu’ magri di quanto non siano nella realta’ e le persone alte di essere piu’ grasse di quello che sono.

La formula proposta e’:

New BMI=(1.3M)/(H^2.5)

dove M e’ la massa in Kg e H e’ l’altezza in metri.

Come il professore spiega essendo il nostro mondo tridimensionale, la presenza dell’esponente 2 e’ anomala. Ci si aspetterebbe infatti un esponente pari a 3. Ma le cose non stanno cosi in quanto le misure di altezza e peso delle persone indicano un’esponente pari a 2.5 anche se egli non riporta alcun dato a supporto. Il pre fattore 1.3 deriva dall’assunzione che una persona di peso medio (non riportato) e altezza pari a 1.69 metri debba avere lo stesso BMI della formula di Quetelet. Ovviamente anche in questo caso la scelta e’ del tutto arbitraria. Nel grafico sottostante e’ riportato l’indice BMI verso l’altezza in metri per una persona di peso pari a 75Kg. Da notare come la nuova formula dia un indice BMI sempre piu’ elevato di quello di Quetelet man mano che l’altezza diminuisce. A parita’ di peso piu’ una persona e’ bassa e piu’ e’ alto il suo indice di massa corporea. La differenza tra i due indici invece e’ meno significativa per le persone piu’ alte dove il nuovo indice e’ solo un 10% piu’ basso (non apprezzabile nel grafico).

Al di la delle differenze che la nuova formula introduce come e’ possibile giustificare un andamento del BMI con un altezza elevata ad un esponente pari a 2.5?

L’indice BMI lo possiamo vedere come il rapporto tra la massa e il volume del corpo umano. Supponiamo di poter assimilare quest’ultimo ad un cilindro di altezza h ed area di base pari a pi(d/2)² dove d e’ il diametro del cerchio che circoscrive le spalle e pi e’ la costante pi greco. Il volume di questo cilindro e’ dato da:

V=pi*h(d/2)² (*)

Se assumiamo che d~h^2/3 allora il rapporto M/V e’:

M/V=(4M/pi)*h^7/3=(1.27M)/h^2.33

che e’ molto prossimo alla formula presentata dal professore Trefethen.

Ma l’assunzione che la larghezza delle spalle scali con l’altezza elevata a 2/3 e’ corretta? L’unico data base con dati di statura e diametro del corpo umano che sono riuscito a trovare sul web e’ un vecchio articolo del Dr. Magnanini del 1900. Utilizzando la tabella N. 3 in esso riportata ho ottenuto una relazione molto prossima a quella che ho ipotizzato sia per il diametro verso l’altezza che per il volume verso l’altezza. Ci si rende conto che questi dati sono molto vecchi e che andrebbero confermati con valori piu’ recenti. Ma al momento e’ il meglio che ho potuto fare.

L’assunzione che nella formula del BMI vada considerato un esponente 2.5 (o meglio 2.33?) anziche’ 2 significa assumere che il volume del corpo umano scala come un frattale di dimensione pari a ~2.5. L’esponente 2.5 indica che il corpo umano non e’ assimilabile ne ad un piano ne ad un cubo, ma sta nel mezzo. Questo non ci deve sorprendere in quanto sappiamo che tutti noi siamo dei frattali. I nostri polmoni, il nostro sistema circolatorio, il nostro cervello sono tutte strutture frattali. La geometria frattale permette di avere figure geometriche con area finita e perimetro infinito, volume finito e superficie infinita. La maggior parte degli oggetti naturali sono composti da molti differenti tipi di frattali intrecciati uno nell’altro, ed ognuno con una sua dimensione

Il tipo di relazione ipotizzata tra il volume e l’altezza (o equivalentemente tra diametro ed altezza) e’ molto comune in biologia e’ prende il nome di relazione allometrica. A differenza delle relazioni isomeriche dove la variabile y e una x sono legate tra loro in modo lineare (cioe’ y=kx) quelle allometriche mostrano una dipendenza non lineare (y=bx^a con a≠1). Per capire meglio il concetto basta dare un occhiata alle due immagini sottostanti. Assimilando l’albero ad un triangolo in caso di relazione isomerica significa che col trascorrere del tempo i tre lati aumenteranno tutti dello stesso fattore, mentre questo non e’ vero nel caso delle relazioni allometriche.

 

Relazione isomerica

Relazione allometrica

Le relazioni allometriche del tipo potenza sono una classe di relazioni molto importanti in quanto hanno la proprieta’ di non avere una lunghezza di scala particolare (infatti si chiamano scale-free) e valgono per diversi ordini di grandezza. Oggetti invarianti per scala hanno lo stesso aspetto quando vengono riscalati in modo opportuno (...di nuovo i frattali).

Ecco perche’ le relazioni allometriche sono delle leggi di potenza e non un esponenziale. Infatti nel caso che

Y=bx^a

Se riscaliamo la x in rx si ha

Y=b(rx)^a=br^ax^a=b’x^a

che ha la stessa forma funzionale iniziale. Nel caso invece di una legge esponenziale si ha:

y=be^-ax

e riscalando la x in rx si ha:

y=be^-arx

che come si vede non e’ la stessa forma iniziale in quanto quest’ultima ha una scala caratteristica data da 1/ar contro la scala 1/a di quella iniziale. Una relazione allometrica molto famosa e’ quella che va sotto il nome di legge di Gutenberg-Richter che lega l’intensita’ dei terremoti espressa in magnitudo verso la frequenza con con cui i terremoti si presentano. Essendo scale-free la relazione vale per i terremoti di piccola magnitudo fino ad arrivare a quelli catastrofici. Essa ci dice che ci sono tanti terremoti di piccola intensita’ e raramente quelli catastrofici.

La super-formula della Natura

Da sempre la forma delle piante e degli organismi ha  affascinato e incuriosito scienziati e ricercatori di tutto il mondo. In natura sono molto comuni le forme sferiche, circolari e cilindriche anche se non mancano forme anche molto piu’ complesse.

Molte di queste oggi possono essere descritte tramite degli appropriati algoritmi capaci di generare delle strutture virtuali. Tuttavia non e’ possibile trovare un algoritmo che riesca a descrivere esattamente una struttura naturale.

Nel 2003, comunque, un botanico belga, Johan Gielis, ha scoperto una “super-formula” capace di descrivere molte figure geometriche presenti in Natura semplicemente variando alcuni parametri caratteristici.

Per un certo valore di tali parametri si ottiene un cerchio, per un altro un quadrato, per un altro ancora un triangolo, e cosi via. Gielis, nel suo articolo pubblicato sul giornale, American Journal of Botany, mostra come molte delle forme della Natura, possono essere interpretate come dei semplici cerchi modificati.

La formula e’ data da:

Si tratta dell’equazione parametrica di una curva espressa in coordinate polari, dove r e’ il raggio e theta  l’angolo. Al variare dei parametri a, b, m, n1, n2 e n3 questa curva puo’ trasformarsi in quadrati, cerchi, ellissi, e tante altre figure da scoprire.

La variabile m definisce i zero-goni (m=0), mono-goni (m=1) e bi-goni (m=2) come anche  triangoli, quadrati e poligoni con un numero di simmetrie rotazionali maggiore. Il valore di m permette agli assi ortogonali di piegarsi all’interno e all’esterno come in un ventaglio.

I valori di n1 e n2 determinano se la forma e’ iscritta o circoscritta dal cerchio unitario. Per n2=n3<2 la forma e’ iscritta (sotto-poligoni) mentre per n2=n3>2 la forma e’ circoscritta dal cerchio unitario (super-poligoni).

Nelle tabelle di seguito vengono mostrate alcune forme che possono essere generate con la super-formula.

Esempio di varie forme ottenute con la super-formula per diversi valori dei suoi parametri

Famiglie di curve generate dalla super-formula con a=b=1, e valori di n1=n2=n3 che vanno da 1 a 8.

Una grande varieta’ di forme dai diversi regni della natura (come per esempio il regno animale e vegetale) possono essere modellate con la super-formula. Mai nessuno era riuscito ad inglobare in una singola formula cosi tante forme diverse in Natura come si puo’ vedere nella figura 3. Le diverse forme della Natura, in questo caso, altro non sono che il risultato di una combinazione di numeri. Un’ appropriata estensione della super-formula permette di descrivere anche forme piu’ complesse ed irregolari che si trovano nel nostro mondo.

Ricorrendo alle parole del suo scopritore Gielis possiamo dire che: la super-formula permette di catturare la semplicita’ matematica e la bellezza di molte forme naturali che differiscono semplicemente per il valore di 5 parametri; essa permette una semplificazione della complessita’ di certe forme e di acquistare una nuova conoscenza sulla simmetria della Natura. Visto che c’e’ una perfetta corrispondenza con le forme naturali, continua Gielis, e’ possibile postulare che la super-formula riveli la geometria base della Natura e quindi essa possa diventare un giorno un potente mezzo per studiare il mondo intorno a noi.

Al momento ancora non e’ chiaro se la super-formula di Gielis avra’ un impatto o no sulle attuali teorie biologiche riguardanti le forme e le simmetrie naturali. Cio’ nondimeno, questa formula fornisce a tutti delle nuove opportunita’ per divertenti e colorate esplorazioni grafiche.

La straordinaria coincidenza tra le forme della Natura e quelle della super-formula.

L’asimmetria del tempo.

 

Analizzando i dati collezionati in 10 anni di esperimenti (miliardi di collisioni tra particelle) i ricercatori della collaborazione Babar, hanno trovato che particelle di un certo tipo (chiamate mesoni Bo) si trasformano in particelle di un altro tipo con ritmi diversi a secondo della direzione del tempo, una violazione della simmetria del tempo ed una conferma che qualche processo subatomico ha una direzione preferenziale del tempo. I dati sono stati pubblicati sul giornale Physical Review Letters. Si tratta di risultati significativi con un errore minore di 1 su 10^43 (ben oltre la soglia per dichiarare una scoperta).

Nell’immagine semplificata riportata qui sotto, due diversi mesoni B stanno passando da uno stato all’altro (rappresentato dai diversi colori); comunque il B-blu cambia nel B-rosso piu’ rapidamente di quanto faccia il rosso-B in blu-B (un processo che va indietro nel tempo come mostrato dall’orologio al contrario). Per queste trasformazioni il tempo e’ stato provato essere asimmetrico. I cambiamenti avvengono con un ritmo diverso a seconda della freccia del tempo in accordo con I risultati dell’esperimento Babar.

Vediamo un attimo che cosa e’ la collaborazione Babar. Si tratta di un esperimento designato per studiare alcune delle questioni fondamentali dell’Universo esplorando I suoi costituenti fondamentali: le particelle elementari. Originariamente l’esperimento era stato realizzato per spiegare quali fossero le differenze tra materia e antimateria e del perche’ l’Universo contiene piu’ materia che antimateria. Ma durante gli anni di servizio, Babar ha fornito altre risposte comunque fondamentali per la comprensione dell’Universo come:

• Ci sono altre particelle oltre a quelle gia’ scoperte?
• Come e’ possibile migliorare la nostra comprensione delle proprieta’ delle particelle e di come loro interagiscono?
• Le particelle fondamentali si legano insieme in modi che noi ancora non conosciamo?
• Quali sono I parametri che descrivono il mondo delle particelle?
• Le particelle di materia oscura interagiscono con le normali particelle in qualche altro modo oltre che con la gravita’?

Ma come funziona l’esperimento Babar?

Utilizzando l’acceleratore SLAC si fanno scontrare elettroni e positroni (elettroni con carica positiva) a differenti energie, generando dei mesoni B che vivono per un corto periodo di tempo prima di decadere (vedi schizzo sottostante). Gli esperimenti per stabilire l’asimmetria del tempo sono stati fatti con questi mesoni B.

Gran parte delle nostre conoscenze fisiche derivano dalla nozione di simmetria. La proprieta’ fondamentale di simmetria alla base del cosiddetto modello standard e’ descritta dal teorema CPT L’acronimo si riferisce a delle particolari trasformazioni:

1) Charge conjugation: scambio della carica da positiva a negativa e viceversa

2) Parity operation: scambio della destra con la sinistra e viceversa (e’ come guardare la realta’ allo specchio)

3) Time reversal: fare andare indietro il tempo nel senso di sostituire nelle relazioni fisiche tutte le t con –t).

Si presume che le leggi della fisica siano simmetriche rispetto alle trasformazioni CPT cioe’ debbano rimanere invariate (le stesse) quando applichiamo l’operazione CPT. Ma cosa dovrebbe accadere alla materia se ad essa applichiamo le trasformazioni CPT? Dovremmo ottenere dell’antimateria.

Per ogni particella della materia ordinaria deve esistere una particella di antimateria con la stessa massa, vita media e spin ma con carica e momento magnetico opposto. 
Un esempio e’ costituito dai positroni o antielettroni e dagli antiprotoni (dei protoni negativi) che insieme formano un atomo di antidrogeno.  

Ma perche’ e’ cosi importante il teorema CPT e la sua eventuale violazione? La risposta sta nell’asimmetria tra materia e antimateria presente nel nostro universo. Cerchiamo di approfondire questo tema.

La materia orindaria come tutti sanno e’ fatta di atomi che a loro volta sono costituiti da un nucleo centrale con degli elettroni che gli orbitano intorno. I nuclei a loro volta sono fatti di protoni e neutroni i cui costituenti finali sono i cosiddetti quarks (up e down in diverse combinazioni).In definitiva quindi tutto cio’ che e’ all’interno del nostro universo e’ fatto di quarks ed elettroni. Queste sono quelle che noi chiamiamo le particelle elementari.

Oltre alla materia esiste anche quella che I fisici chiamano l’antimateria. Essa e’ uguale alla materia ordinaria a differenza della carica elettrica che e’ di segno opposto. Da un punto di vista teorico e’ possibile avere degli antinuclei, antiatomi e anche anti-solidi. Ma dov’e’ l’antimateria nell’universo? Secondo la meccanica quantistica che regola I fenomeni a scala atomica e subatomica quando materia e antimateria si incontrano si annichilano trasformando la loro energia in luce.

>Anche se l’antimateria sembra essere qualche specie di materia esotica, essa viene utilizzata per esempio negli ospedali per la PET (positron emission tomography).

Ritornando al nostro universo, perche’ oggi la stragrande maggioranza degli oggetti sono fatti di materia e non di antimateria? Poiche’ materia ed antimateria si annichilano, subito dopo il Big Bang essendo la quantita’ di materia ed antimateria la stessa noi avremmo dovuto avere un universo vuoto con all’interno solo luce. Ma noi sappiamo che non e’ cosi. E allora come sono andate le cose?

La risposta sembra venire dai risultati sperimentali di Babar che indicano che molto probabilmente le leggi della fisica per la materia e antimateria non sono esattamente le stesse avendo cosi all’inizio del nostro universo uno sbilanciamento piccolo verso la materia e con la scomparsa dell’antimateria dopo l’interazione con la materia ordinaria con conseguente emissione di luce. E questa asimmetria potrebbe essere dovuta proprio alla violazione delle trasformazioni CP e CPT. Qui di seguito un esempio di trasformazione CP utilizzando un quadro di Escher.