Possono i numeri avere una forma geometrica?
Anche se e’ chiaro di no, alcuni di essi possono essere rappresentati da punti disposti come figure geometriche regolari. Questi numeri vengono chiamati numeri figurati o numeri poligonali.
I numeri figurati più conosciuti sono i numeri quadrati, cioè i numeri 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121,…….
Essi si chiamano così perché possono essere disposti all’interno di quadrati come quelli riportati sotto.
Gli angoli rossi sono quelli che gli antichi Greci chiamavano “gnomon”. Ogni quadrato e’ formato dal quadrato precedente indicato in blu più lo gnomon. I numeri appartenenti allo gnomon dei numeri quadrati sono: 1, 3, 5, 7, 9, 11,…. Praticamente i numeri dispari.
I numeri figurati più conosciuti sono i numeri quadrati, cioè i numeri 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121,…….
Essi si chiamano così perché possono essere disposti all’interno di quadrati come quelli riportati sotto.
Gli angoli rossi sono quelli che gli antichi Greci chiamavano “gnomon”. Ogni quadrato e’ formato dal quadrato precedente indicato in blu più lo gnomon. I numeri appartenenti allo gnomon dei numeri quadrati sono: 1, 3, 5, 7, 9, 11,…. Praticamente i numeri dispari.
Da qui discende facilmente che l'ennesimo numero quadrato e’ dato dalla somma del quadrato precedente piu' i numeri dispari consecutivi. Allo stesso modo e’ possibile trasformare in termini matematici quello che abbiamo visto con la rappresentazione geometrica, cioè che e’ vera la seguente formula ricorsiva per i numeri quadrati Q:
Qk+1=Qk+2k+1
dove k=0, 1, 2, 3, 4…. e Q0=0
Qk+1=Qk+2k+1
dove k=0, 1, 2, 3, 4…. e Q0=0
Il numero di rappresentazioni di un numero n tramite k quadrati, distinguendo il segno e l’ordine, viene indicato con rk(n); si tratta di una funzione di n chiamata la funzione della somma dei quadrati. Per esempio, consideriamo il numero di modi in cui e’ possibile rappresentare il numero 5 come somma di 2 quadrati:
e quindi r2(5)=8. Allo stesso modo il numero 4 puo’ essere scritto come somma di tre quadrati come segue:
e quindi r2(4)=6.
Diversi grandi matematici hanno contribuito a determinare un’espressione analitica di questa funzione. Jacobi ci riusci’ nel 1829 per k=2,4,6, e 8. La soluzione per k=10 e 12, invece, fu trovata da Liouville e in seguito da Eisenstein. Glaisher nel 1907, riusci a sviluppare una tabella di r2s(n) per 2s fino a 18. Il grande Ramanujan, estese il risultato di Glaisher fino a 2s=24.
La funzione r2(n) a volte indicata come r(n) e’ intimamente connessa al problema del cerchio di Gauss.
Questo problema consiste nel contare, per un cerchio di raggio r, il numero dei punti del reticolo N(r), all’interno dei confini del cerchio (confine incluso) con centro nell’origine (vedi figura 1).
L’esatta soluzione di questo problema e’ data dalla formula:
indica la parte intera del numero n. I primi valori di N(r) per r=0,1,2,3…. sono 1, 5, 13, 29, 49, 81, 113, 149…….
Figura 1: Problema del cerchio di Gauss.
L’esatta soluzione di questo problema e’ data dalla formula:
indica la parte intera del numero n. I primi valori di N(r) per r=0,1,2,3…. sono 1, 5, 13, 29, 49, 81, 113, 149…….
La serie N(r) e’ legata alla funzione della somma di due quadrati r(n) in quanto si puo’ dimostrare che:
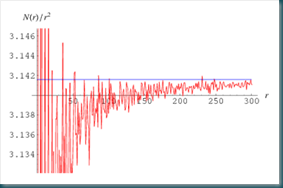
In figura 2, viene riportata la rappresentazione della funzione N(r)/r2 in funzione di r. Osservare l’andamento asintotico della funzione dopo aver attraversato una zona per bassi valori di r con grosse oscillazioni.
I numeri 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, ... sono invece i cosiddetti numeri triangolari in quanto possono essere rappresentati tramite triangoli regolari.
Se con Tk indichiamo il k-esimo numero triangolare si può verificare che vale la seguente relazione:
Figura 2: Andamento del rapporto N(r) e il quadrato di r
I numeri 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, ... sono invece i cosiddetti numeri triangolari in quanto possono essere rappresentati tramite triangoli regolari.
Se con Tk indichiamo il k-esimo numero triangolare si può verificare che vale la seguente relazione:
con T0=0.
Questa relazione ricorsiva può essere espansa per dimostrare che il k-esimo numero triangolare altro non e’ che la somma di tutti numeri da 1 a k.
Poiché la somma dei primi k numeri e’ data da k(k+1)/2 possiamo scrivere che:
Osservare che a partire dai numeri triangolari si possono ottenere i numeri quadrati. E’ facile, infatti, dimostrare che:
Schematicamente questa relazione può essere rappresentata nel seguente modo:
Qui l’n-1_esimo numero triangolare e’ rappresentato dai triangoli bianchi, l’n_simo numero triangolare dal numero di triangoli neri mentre il numero totale dei triangoli e’ l’ennesimo numero quadrato.
Un'altra relazione dimostrata da Conway e Guy nel 1996, lega i numeri triangolari a quelli quadrati.
Si può verificare che essa e’ vera osservando che e’ sempre possibile dividere un quadrato in 8 triangoli a parte un tassello.
Nel 1638, Fermat propose che ogni numero intero positivo, e’ la somma di almeno tre numeri triangolari, quattro numeri quadrati, cinque numeri pentagonali e cosi via.
Si può verificare che essa e’ vera osservando che e’ sempre possibile dividere un quadrato in 8 triangoli a parte un tassello.
Nel 1638, Fermat propose che ogni numero intero positivo, e’ la somma di almeno tre numeri triangolari, quattro numeri quadrati, cinque numeri pentagonali e cosi via.
Egli riportò di avere una dimostrazione, anche se essa non e’ mai stata trovata.
In seguito Gauss provò che il caso dei numeri triangolari era vero e annoto’ l’evento sul suo diario (10 Luglio 1796) con la scritta ormai famosa:
Il caso dei numeri quadrati fu dimostrato da Jacobi e Lagrange nel 1772, mentre l’intero teorema e’ stato dimostrato solo nel 1813 da Cauchy.
Il caso dei numeri quadrati fu dimostrato da Jacobi e Lagrange nel 1772, mentre l’intero teorema e’ stato dimostrato solo nel 1813 da Cauchy.
Allo stesso modo dei numeri triangolari e numeri quadrati e’ possibile costruire numeri pentagonali, esagonali, ettagonali ….. In generale possiamo parlare di numeri poligonali. Questi numeri sono caratterizzati da due parametri: il numero E dei vertici e il numero k del rango (il primo, secondo, terzo etc). Il minimo valore per questi due parametri e’ 3 ed 1 rispettivamente.
Con G(E,k) indichiamo il numero poligonale con E vertici e allo stadio k.
I numeri:
G(3,k) rappresentano i numeri triangolari
G(4,k) i numeri quadrati
G(5,k) i numeri pentagonali
G(6,k) i numeri esagonali
G(7,k) i numeri ettagonali
G(8,k) i numeri ottagonali
e cosi via. I numeri poligonali sono numeri i cui punti che li rappresentano possono essere disposti all’interno di poligoni regolari. Allo stadio k=1 ogni numero poligonale e’ costituito da un solo punto, cioè G(E,1)=1. Per k maggiore o uguale a 2 il numero poligonale appartenente alla famiglia G(E,k) evolve da quello precedente G(E,k-1) mettendo insieme una “catena” aperta di nuovi punti ai k-2 lati del vecchio pattern cosicché i vertici andranno a formare un nuovo poligono con esattamente k punti su ognuno dei suoi lati.
e cosi via. I numeri poligonali sono numeri i cui punti che li rappresentano possono essere disposti all’interno di poligoni regolari. Allo stadio k=1 ogni numero poligonale e’ costituito da un solo punto, cioè G(E,1)=1. Per k maggiore o uguale a 2 il numero poligonale appartenente alla famiglia G(E,k) evolve da quello precedente G(E,k-1) mettendo insieme una “catena” aperta di nuovi punti ai k-2 lati del vecchio pattern cosicché i vertici andranno a formare un nuovo poligono con esattamente k punti su ognuno dei suoi lati.





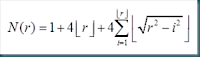
















Nessun commento:
Posta un commento