Quanto sono frequenti i terremoti? C’e’ la possibilita’ di prevederli?

La domanda piu’ frequente rivolta ai sismologi dalla gente comune e’ la seguente: e’ possibile prevedere i terremoti? E se no perche’?

A parte i giudici dell’Aquila, nessuno al mondo puo’ affermare che i terremoti siano prevedibili. Nel corso di questo articolo cercheremo di capire il perche’. Quello che i geofisici hanno capito in anni di studio e’ che la dinamica della Terra puo’ essere modellizzata con la tettonica delle placche e che i terremoti non sono l’effetto di eventi casuali ma piuttosto il prodotto finale di una lunga serie di movimenti e stress che avvengono all’interno della terra in punti specifici.

Quindi detto cosi, i terremoti dovrebbero essere prevedibili. Ma nonostante tutti gli sforzi dei ricercatori  non esiste ancora un metodo che riesca a predire con assoluta certezza, il giorno, l’ora e la magnitudo di un terremoto. La Terra  e’ un sistema troppo complesso (non complicato) per riuscire a modellare il suo comportamento a livello microscopico. Molti scienziati, pensano che questo problema sia praticamente irrisolvibile. Prima di un terremoto, gli stress di una faglia (frattura tra due blocchi di roccia) possono rimanere in equilibrio critico per un tempo anche molto lungo. Riuscire a sapere quando una faglia subira’ il movimento relativo delle parti ad essa adiacenti (cioe’ quando avviene un terremoto) dipende da cosi tanti fattori aggiuntivi (alcuni microscopici altri macroscopici) oltre agli stress che la previsione diventa impossibile.

Lungo una faglia ci possono essere essenzialmente tre movimenti relativi che vanno sotto il nome di faglia normale, faglia inversa e faglia trascorrente rispettivamente.

 

Un’analogia puo’ essere quella della previsione dei movimenti della sabbia all’interno di una clessidra. Possiamo predire con grande accuratezza quanto tempo sara’ necessario alla sabbia per svuotare la parte superiore della clessidra. Possiamo anche predire la forma che la sabbia prendera’ una volta caduta nella camera inferiore ma non possiamo predire dove andra’ a finire ogni granello quando esso cade attraverso il foro della clessidra.

Il primo ad analizzare la dinamica di un mucchietto di sabbia e’ stato il fisico danese Per Bak che grazie ai suoi studi ha scoperto come molti sistemi dinamici naturali, fuori dall’equilibrio, possono auto-organizzarsi in uno stato critico governato da una legge di potenza.

L’apparato sperimentale ideato da Bak molto simile ad una clessidra è costituito da un piatto sul quale vengono fatti cadere uno alla volta dei granelli di sabbia. Gradualmente i granelli caduti formano un mucchietto i cui pendii lentamente diventano sempre più ripidi. Quando la pendenza supera un certo valore si formano delle valanghe. Man mano che si aggiunge altra sabbia la dimensione media di queste valanghe aumenta e alcuni granelli finiscono oltre il bordo del piatto. Il mucchietto cessa di crescere quando la quantità di sabbia aggiunta è in media uguale a quella che cade al di fuori del piatto ed è a questo punto che il sistema ha raggiunto lo stato critico.

A questo punto aggiungendo al mucchietto anche un solo granello di sabbia si possono innescare valanghe di qualunque dimensione.

Tracciando un grafico in scala logaritmica in cui si pone sull’asse y il numero di valanghe e sull’asse x la loro dimensione (il numero di granelli coinvolti) si ottiene una retta: questo vuol dire che il fenomeno e governato da una legge di potenza.

Se la forma del mucchietto è tale per cui la pendenza è inferiore a quella critica le valanghe sono più piccole di quelle che si verificano nello stato critico permettendo così alla sabbia di raggiungere lo stato critico. Se la pendenza è superiore a quella critica le valanghe sono più imponenti di quelle allo stato critico facendo crollare il mucchietto di sabbia fino allo stato critico.

I mucchietti supercritici proprio come quelli subcritici sono attratti verso lo stato critico. Quindi il sistema si auto-organizza in uno stato critico dove anche una piccola perturbazione puo’ generare una catastrofe. Questo modello sembra governare terremoti, valanghe, tsunami, economia e altri fenomeni. L’auto-organizzazione implica la validita’ di una legge di potenza, il che significa che non esiste nessuna scala particolare, cioe’ i terremoti di bassa intensita’ sono molto piu’ frequenti di quelli catastrofici. Il meccanismo alla base dei terremoti e’ lo stesso sia per quelli catastrofici che per quelli di bassa intensita’.

Sebbene la previsione dei terremoti al momento e’ troppo difficile (e forse lo sara’ per sempre come io credo) e’ possibile calcolare la probabilita’ che avvenga un terremoto in una particolare regione della Terra. Questo fa si che i progettisti degli edifici in regioni a rischio seguano delle regole piu’ stringenti rispetto a quelle utilizzate in zone a basso rischio sismico.

Qualsiasi mappa della sismicita’ mondiale come quella mostrata qui sotto, mostra che i terremoti per la maggior parte tendono a formare dei clusters con il 90% di essi disposti lungo le frontiere delle placche terrestri.

 

Occasionalmente comunque, ci sono sequenze di terremoti che capitano in posti dove non era stata osservata nessuna sismicita’ fino ad allora. Con molta probabilita' questo e’ dovuto al fatto che gli strumenti per registrare i terremoti sono nati circa 100 anni fa e quindi in zone di bassa sismicita’ non c’e’ stato tempo a sufficienza per raccogliere una quantita’ di dati statisticamente significativi. Ad ogni modo la sfida maggiore per i geofisici non e’ tanto l’identificazione delle regioni a rischio quanto riuscire a stimare la frequenza e l’energia degli eventi sismici di una particolare regione.

L’intensita’ di un terremoto e’ espressa in magnitudo M che e’ legata all’energia E rilasciata dall’evento sismico ( log₁₀E = 11.8 + 1.5M ). Un aumento della magnitudo di un’unita’ implica un aumento dell’energia di un fattore 32. Fortunatamente per gli esseri umani i terremoti catastrofici sono molto meno frequenti di quelli piccoli. Nella tavola seguente sono riportate le intensita’ espresse in magnitudo dei terremoti e la loro media annuale. Per esempio mediamente in un anno avremo sulla terra un terremoto catastrofico con una magnitudo superiore a 8.

 

 

Il numero di vittime generato da un terremoto non dipende necessariamente dalla loro magnitudo. Terremoti moderati possono generare piu’ vittime di un terremoto forte se questi avvengono in aree dove le costruzioni sono fatiscenti o non costruite con criteri antisismici. Una frattura generata nel suolo da un terremoto aumenta approssimativamente con la sua magnitudo secondo la relazione:

log10(Area) = (1.05M)-2.95.

Un terremoto di magnitudo 5 generera’ una frattura con un raggio di circa 8 Km, un terremoto di magnitudo 6 invece una frattura con un raggio di circa 30 Km e un terremoto di magnitudo 8 una frattura con un raggio di circa 300 Km.

La distribuzione del numero di terremoti in funzione della magnitudo e’ stata trovata seguire una legge di potenza: quando graficata su una scala semilogaritmica la distribuzione e’ lineare. I primi ad accorgersi di questo comportamento furono Gutenberg e Richter nel 1944 che introdussero la famosa equazione che oggi porta il loro nome:

log10 N = a – bM

Qui N e’ il numero cumulativo di terremoti con magnitudo superiore o uguale ad M. a e b sono due costanti. Il grafico sottostante e’ un esempio di legge G-R per I terremoti registrati in Italia dal 1900 al 2006. Il grafico mostra la distribuzione Frequenza-Magnitudo (FMD in inglese) in accordo al database dell’INGV.

La costante b indica la pendenza della FMD e descrive la relativa intensita’ dei terremoti. Un valore alto di b indica una larga proporzione di terremoti deboli e viceversa. Il valore a (intercetta della retta con l’asse x) indica l’attivita’ sismica. Osservare che per piccole magnitudo la retta non segue la legge di potenza G-R in quanto e’ difficile riuscire a captare i terremoti di piccola intensita’. Nel nostro caso il valore di b e’ circa 1.1 e quello di a circa 8.65 considerando solo I terremoti con M>=5.

 

 

FMD degli eventi registrati in Italia dal 1900 al 2006 ( dati estratti dal database del INGV)

Correlazione tra il logN e magnitudo per I sismi avvenuti in  Italia dal 1900 al 2006. 

La pendenza del fit lineare rappresenta il coefficiente b (1.132) della relazione G-R e l’intercetta il valore a (8.656). Le equazioni fin qui descritte ci dicono anche un’altra cosa molto importante: i terremoti di bassa intensita’ non possono essere considerati come una valvola di sfogo per evitare i terremoti catastrofici. In una regione, il fatto di avere tanti terremoti di piccola intensita’ non esclude la possibilita’ che ci possa essere un terremoto catastrofico. Questo perche’ come abbiamo visto passando da un terremoto di magnitudo M ad uno di magnitudo M+1 comporta un’energia piu’ grande di un fattore 32 rispetto al terremoto di magnitudo M. Allo stesso modo pero’ la legge G-R prevede che passando da una magnitudo M ad M-1 il numero di terremoti aumenti di un fattore 10. Quindi ci possiamo aspettare solo 10 terremoti con magnuitudo M-1 rispetto ai 32 necessari per smaltire l’energia di un terremoto di magnitudo M. Ovviamente se il parametro b della legge G-R fosse molto vicino 1.5 allora sarebbe possibile scaricare l’energia accumulata dalla crosta terrestre tramite tanti piccoli terremoti.

Il parametro b dell’equazione di G-R e’ molto prossimo ad 1 anche se non per tutte le zone del mondo. Basta per esempio considerare i terremoti avuti dal 2009 al 2013 nella regione Abruzzo per vedere che il parametro b e’ pari a 0.975 con una variazione del 14% rispetto al valore ottenuto considerando l’Italia intera. Questo significa che l’Abruzzo e’ una regione dove e’ piu’ alta la probabilita’ di terremoti rispetto alla media italiana essendo il valore del parametro b piu’ piccolo. Osservare come il fattore moltiplicativo dipenda da 10^-b e quindi piccole variazioni in b comportano grandi variazioni nel numero di terremoti.

 

FMD degli eventi sismici registrati in Abruzzo dal 2009 al 2013

Correlazione logN e magnitudo per I terremoti dell’Abruzzo tra il 2009 e il 2013. La pendenza del fit lineare rappresenta il coefficiente b (0.975) della relazione G-R e l’intercetta il valore a (5.853)

 

L’importanza della distribuzione FMD sta nel fatto che essa puo’ essere utilizzata per fare previsioni probabilistiche del pericolo di un sisma.  Riscrivendo la legge  di  G-R possiamo calcolare la probabilita’ che si verifichi un terremoto di magnitudo M maggiore di un certo valore di soglia Mt:

P(M>M_t) = 10(a-bM)/ dT

dove dT e’ il periodo temporale di osservazione (1900-2006 = 106 anni nel nostro caso). Usando a=8.656 e b=1.132 per il caso dei terremoti italiani dal 1900 al 2006 troviamo che un terremoto con magnitudo 6 o maggiore ha una probabilita’ annuale di circa 18%. In altre parole in Italia ci possiamo aspettare un terremoto con magnitudo di 6 o piu’ circa ogni 6 anni. Questo valore e’ confermato dall’analisi statistica dei terremoti Italiani con magnitudo maggiore o uguali a 6 nel periodo in considerazione. Come si vede dal grafico l’intervallo di tempo medio e’ di 6.57 anni, molto prossimo ai ~6 anni trovati con la legge di G-R. Dal grafico della probabilita’ cumulata si osserva anche che c’e’ una probabilita’ del 90% di avere un terremoto di intensita’ uguale o superiore a 6 nell’arco di 10 anni.

 

 

Come  gia' detto e’ molto importante il valore di a e b nella  legge  di   G-R. Qui sotto l’andamento della probabilita’ annuale di avere un terremoto di magnitudo maggiore o uguale a 6 in funzione del valore di b avendo assunto a=8.656. Un valore di b molto piccolo fa si che aumenti significativamente la probabilita’ annuale di un terremoto. Osserviamo anche che con un valore di b superiore a ~1.4 la probabilita’ di avere terremoti di intensita’ uguale o superiore a 6 e’ praticamente nulla. Da tutto cio’ si capisce che e’ molto importante stabilire con buona precisione il valore di a e b di una data regione per avere previsioni affidabili. Ma questo non e’ un impresa facile; questi valori sembrano cambiare non solo spazialmente ma anche temporalmente. Sono stati individuati infatti fino a 4 tipi di comportamento nel tempo. Nel primo il valore di b diminuisce prima dei grandi sismi. Nel secondo il valore di b prima aumenta e poi improvvisamente diminuisce prima di un evento catastrofico. Nel terzo modello il valore di b varia durante tutta la fase di assestamento mentre nel quarto modello il valore di b varia significativamente tra una regione e l’altra e durante lunghi periodi di tempo indipendentemente dall’intensita’ del sisma.

 

Andamento della probabilita’ annuale di un terremoto di magnitudo maggiore o uguale a 6, 7, 8 e 9 in Italia in funzione del valore di b avendo fissato a=8.656

Un esempio per tutti. In una piccola cittadina della California, Parkfield, sono stati documentati 6 terremoti di magnitudo 6 tra il 1857 e il 1966. In base a quanto detto ci si aspettava un terremoto di intensita’ pari a 6 intorno al 1988. Ma questo terremoto non c’e’ mai stato almeno fino ad oggi.

 

In prima approssimazione i terremoti non mostrano nessuna regolarita’ temporale e quindi e’ giusto assumere come distribuzione dei tempi di attesa una distribuzione di Poisson. Se mediamo i terremoti su una regione abbastanza vasta questa assunzione e’ pienamente verificata. Per esempio, il tasso globale di terremoti di magnitudo maggiore di 5 e’ quasi costante come richiesto da una distribuzione di Poisson.

 

Numero annuale di terremoti con magnitudo maggiore di 5 come ricavato dal database sella NEIC.

 

Questa distribuzione fu scoperta dal francese Simeon Denis Poisson nel 1837; essa permette il calcolo della probabilita’ del verificarsi o no di un certo numero di eventi in un intervallo temporale definito purche’ tali eventi si manifestino con un un tasso medio costante e siano indipendenti nel tempo.

Secondo quanto trovato da Poisson, la probabilita’ P di avere n terremoti in un intervallo temporale t e’ data da:

P(n, t,dt) = (t /dt )ⁿ e^{-t/ dt}/ n!

dove dt e’ il tempo medio tra un terremoto e l’altro (il suo inverso e’ il tasso). Quindi la probabilita’ che non si verifichi nemmeno un terremoto in un intervallo temporale t e’ data da:

P(0, t, dt) = e^{-t/d t}

oppure la probabilita’ che se ne verifichi almeno 1 e’ data da:

P(n>=1, t,dt) =1- P(0, t, dt) = 1- e^{-t/ dt}

Usando per esempio la distribuzione di Poisson per eventi con magnitudo maggiore di 7 e un tasso di 0.05 terremoti al giorno possiamo stabilire che la probabilita’ che ci sia un evento in 14 giorni e’ del 50% e del 90% in 46 giorni.

Comunque le scosse di assestamento che si presentano dopo ogni evento principale e gli sciami sismici sono chiari eventi che violano l’assunzione di una distribuzione poissoniana. Dopo una scossa principale ci saranno sempre delle scosse di assestamento che si verificano nelle vicinanza della frattura principale

Un esempio e’ il terremoto dell’Aquila dove dopo la scossa principale avvenuta il 6 Aprile 2009 con magnitudo 6.3 l’attivita’ sismica e’ continuata per anni decadendo secondo la cosiddetta legge di Omori

N=At^-a

dove A ed a sono due costanti, N e’ il numero di scosse e t il tempo trascorso rispetto alla scossa principale.

Dopo questa breve analisi cosa possiamo dire sulla previsione dei terremoti? E’ solo questione di tempo? Oggi non siamo capaci di prevedere i terremoti e chiunque afferma il contrario verra’ smentito dal prossimo catastrofico sisma non predetto. Ma un giorno ci riusciremo? Forse si ma non domani. Forse tra 10, 20 anni o forse mai. La natura per poter essere “creativa” deve stare all’edge del caos. Questo e’ vero per tutti i sistemi complessi che mostrano una grande resilienza e adattabilita’ a spesa dell’imprevedibilita’. Non si puo’ volere tutto dal nostro universo…………

La vita prima della Terra

La legge di Moore, nota a tutti quelli che lavorano nel campo della tecnologia, fu formulata da Gordon Moore, cofondatore di Intel con Robert Noyce in un articolo pubblicato su una rivista specializzata dove illustrava come nel periodo 1959-1965 il numero di componenti elettronici (come per esempio il numero dei transistors) all’interno di un chip raddoppiava ogni anno.

Nel 1975 questa previsione si rivelo’ corretta e prima della fine del decennio i tempi si allungarono a 2 anni, e alla fine degli anni ottanta fu elaborata nella sua versione definitiva, ovvero la complessita’ dei processori raddoppia ogni 18 mesi.

Un processo simile si verifica anche per le pubblicazioni scientifiche. Tra il 1960 e il 1990 queste hanno quasi raddoppiato il loro numero ogni 15 anni. Estrapolando questa correlazione indietro nel tempo si trova che l’inizio delle pubblicazioni scientifiche e’ da ricercare intorno al 1710 che e’ prossimo ai tempi di Isaac Newton (morto nel 1727). Un altro andamento simile alla legge di Moore  si ritrova per il numero di cifre decimali di pi greco come si vede nel grafico sottostante (il numero di cifre decimali conosciute raddoppia ogni 22.5 mesi).
 

L’algoritmo utilizzato per trovare nuove cifre decimali di pi greco si basa su una formula sviluppata dal grande matematico indiano Srinivasa Ramanujan:
 

Questa serie fornisce un incremento di accuratezza di 14 cifre per ogni approssimazione successiva.

Due genetisti, Alexei Sharov del National Institute on Aging in Baltimore, e Richard Gordon del Gulf Specimen Marine Laboratory in Florida, hanno pensato di utilizzare la legge di Moore rimpiazzando i transistors con i nucleotidi, i mattoni del DNA e del RNA, e i circuiti con il materiale genetico.

In questo modo hanno trovato che il rate con cui la vita e’ passata dai procarioti agli eucarioti e poi a creature piu’ complesse come vermi, pesci e mammiferi e’ di circa 376 milioni di anni. Questo significa che la complessita’ delle vita raddoppia ogni 376 milioni di anni.

Estrapolando all’indietro questa relazione e’ possibile individuare quando nel passato esisteva solo una coppia di basi (complessita’ zero) cioe' quando e’ iniziata la vita. Il risultato ottenuto dai due scienziati e’ a dir poco sbalorditivo. La vita ha avuto origine 9.7±2.5 miliardi di anni fa.

Poiche’ si crede che la Terra si sia formata circa 4.5 miliardi di anni fa questo implica che la vita e’ nata prima della Terra in qualche parte dell’Universo a noi sconosciuta e poi migrata sul nostro pianeta. E’ possibile che spore batteriche congelate (che possono sopravvivere per milioni di anni  in queste condizioni estreme) siano arrivate sulla Terra grazie a delle comete o dei meteoriti (panspermia).

Sharov e Gordon sono convinti che la loro ipotesi spiega il paradosso di Fermi secondo il quale se l’universo e’ popolato da vita intelligente perche’ non abbiamo evidenza di cio’?

La risposta potrebbe essere: se la vita ha avuto bisogno di circa 10 miliardi di anni per evolvere al livello di complessita’ associato agli umani, allora noi potremmo essere tra i primi se non i primi esseri intelligenti nella nostra galassia. E questa e’ la ragione del perche’ quando rivolgiamo lo sguardo allo spazio esterno non vediamo segni di altre specie intelligenti.

Ovviamente il risultato dei due genetisti non e’ una dimostrazione scientifica. Non c’e’ modo di conoscere se la complessita’ organica e’ aumentata ad un tasso costante in ogni istante della storia dell’universo. Si tratta semplicemente di un esercizio mentale piu’ che di una teoria. Comunque secondo I due autori la contaminazione con spore batteriche dallo spazio appare l’ipotesi piu’ plausibile per spiegare la comparsa della vita sulla Terra. Secondo Sharov la probabilita’ che la vita sia apparsa prima della nascita della terra e’ del 99% e c’e’ solo un 1% che invece non sia cosi.

Sicuramente si tratta di una idea controversa che suscitera’ molte discussioni tra i teorici evoluzionisti. Allo stesso tempo pero’ e’ un’idea provocante, interessante ed eccitante. Tutte buone ragioni per portare avanti il dibattito che e’ gia’ iniziato.

Secondo alcuni studiosi, infatti nel grafico utilizzato da Sharov e Gordon sono stati inseriti solo alcuni punti scelti accuratamente, non riportando per esempio felci,  cipolle o alcuni protisti semplicemente perche’ avrebbero “rovinato” la correlazione avendo un genoma piu’ grande di quello dei mammiferi. Bisognera’ aspettare per capire chi ha ragione.  

L’articolo originale puo’ essere trovato al seguente link: full report

 

La riconquistata socialita’ dei numeri primi

 

I numeri primi sono diventati meno solitari di quanto si pensasse. Questo grazie all’annuncio del prof. Zhang fatto qualche settimana fa e riguardante la dimostrazione che il numero di primi che nelle loro vicinanze hanno qualche altro primo sono infiniti anche se questa distanza puo’ essere grande fino a 70.000.000.

Questa dimostrazione e’ legata ad una delle piu’ famose congetture sui numeri primi mai risolta: quella dei numeri primi gemelli.

Un numero naturale e’ un primo se e’ divisibile solo per 1 e per se stesso. La sequenza inizia con 2, 3, 5, 7, 11, 13, 17, 19, 23,…… I numeri primi sono gli atomi della Teoria dei numeri, le entita’ indivisibili di cui sono fatti tutti I numeri. In quanto tali essi sono stati oggetto di intensi studi da parte dei matematici. Uno dei primi Teoremi in Teoria dei numeri e’ quello di Euclide che secondo la tradizione provo’ che il numero dei primi e’ infinito.

Ma parlare di infinita’ non basta. Per esempio le potenze di 2 sono infinite e allo stesso tempo sono molto rare. Infatti ce ne sono solo 10 nei primi 1000 numeri naturali (1,2,4,8,16,32,64,128,512). Anche i numeri pari sono infiniti e di sicuro sono meno rari delle potenze di 2 in quanto nei primi 1000 numeri naturali ne abbiamo 500. E’ i numeri primi? Assodato che ne sono infiniti, qual’e’ la loro densita’? Essi si posizionano tra i numeri pari e le potenze di 2. Piu’ comuni delle potenze di 2 ma  meno rari dei numeri pari. Tra i primi N numeri interi, circa N/log(N) sono primi; questo e’ il cosiddetto Teorema dei numeri primi provato alla fine del secolo 19-mo da Hadamard e de la Vallee Poussin. Questo significa che i numeri primi diventano sempre meno comuni man mano che i numeri diventano piu’ grandi anche se la decrescita e’ molto lenta.

Detto cio’ e’ naturale pensare che piu’ un tipo di numero e’ comune e piu’ piccola e’ la distanza tra di essi. Se siamo interessati ai numeri pari, siamo sicuri di trovarne uno ogni 2 numeri naturali. Infatti la gap come si suole indicare la distanza in inglese e’ sempre uguale a 2. Per le potenze di 2 abbiamo una storia completamente diversa. Le distanze successive crescono esponenzialmente e ci sono gaps finite di qualsiasi lunghezza.

Questi 2 problemi sono semplici. La questione delle gap tra i numeri primi invece e’ molto ma molto piu’ complicata. A prima vista sembra che i numeri primi siano disposti a caso tra i numeri naturali ma non e’ esattamente cosi. Infatti la distribuzione dei numeri primi non e’ completamente casuale.

I numeri primi gemelli sono quelli che hanno una distanza di 2 come 3 e 5, 5 e 7, 11 e 13 e cosi via. La piu’ grande coppia di numeri primi gemelli ad oggi conosciuta e’ data da:

3,756,801,695,685 × 2^666,669 + 1 e 3,756,801,695,685 × 2^666,669 – 1

La congettura dei numeri primi gemelli stabilisce che esistono infinite coppie di tali numeri.

Nonostante la sua semplicita’ una dimostrazione di tale affermazione resiste all’attacco di matematici di tutto il mondo fin da quando la congettura venne enunciata nel 1849 dal matematico francese Alphonse de Polignac.

L’aspetto affascinante della Teoria dei numeri e’ proprio questo: le congetture sono cosi’ semplici che possono essere comprese da tutti. Ma dimostrarle e’ tutta un altra storia.

In generale per cercare di aprire un varco in una congettura della Teoria dei numeri i matematici cercano di rispondere a delle domande piu’ semplici che possono aiutare nella dimostrazione delle congettura. Questo e’ vero anche per la congettura dei primi gemelli. Una domanda a cui i matematici hanno cercato di dare una risposta e’ la seguente: esistono infinite coppie di primi con una distanza finita tra loro anche se molto grande e quindi maggiore di 2?

Ed e’ a questa domanda che il professore Zhang dell’Universita’ del New Hampshire afferma di aver dato una risposta definitiva. Infatti egli ha trovato che esistono infinite coppie di primi con distanza minore di 70.000.000 cioe’ in termini tecnici:

lim(n—>∞) inf (p_n+1-p_n)<C

con C=7X10⁶

Per sfortuna dei primi solitari la distanza e’ ancora molto grande; ma Zhang ribadisce che questo e’ un limite superiore ed essere passati dall’infinito a 70 milioni e’ gia’ un grande successo. Inoltre il professore e’ convinto di poter migliorare a breve questo limite e portarlo al di sotto di un milione anche se rimane ben lontano dal 2 della congettura dei primi gemelli.

Il lavoro del professore Zhang e’ stato pubblicato sulla rivista degli Annali di Matematica (Annals of Mathematics) e adesso bisogna aspettare il parere dei matematici che rivisiteranno il lavoro prima di poter cantare vittoria.

In queste ultime settimane un’altra famosa congettura sembra mostrare qualche barlume di speranza per una sua dimostrazione. Si tratta della congettura forte di Goldbach che afferma che ogni numero pari maggiore di 2 e’ la somma di 2 numeri primi. Harald Helfgott (link) della Scuola Normale Superiore di Parigi ha provato un problema legato a questa congettura. Si tratta della congettura debole di Goldbach che stabilisce che ogni numero dispari maggiore di 5 puo’ essere scritto come la somma di 3 primi. Entrambe le congetture furono formulate da Goldbach in una corrispondenza con Eulero. Ovviamente una dimostrazione della congettura di Goldbach indirettamente proverebbe anche quella dispari ma non vale il contrario. Quindi al momento la congettura di Goldbach rimane ancora in attesa di una dimostrazione anche se il risultato di Helfgot e’ un altro tassello importante per la soluzione del puzzle. La dimostrazione di Helfgott (sempre che venga confermata dalla comunita dei matematici) segue il risultato ottenuto da Vinogradov che nel 1937 mostro’ che la congettura debole di Goldbach era vera per ogni n maggiore di una costante e che nonostante tutti gli sforzi era rimasto sempre un numero molto grande da poter permettere la verifica della congettura per gli interi al di sotto di questa costante con i computer piu’ potenti al mondo.

La bellezza dell’invarianza di scala

 

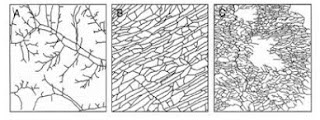
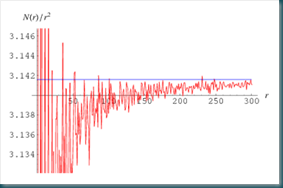
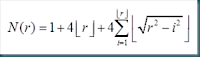In questo nuovo post parleremo di frattali. Si tratta di oggetti geometrici che presentano una struttura complessa e dettagliata ad ogni livello di ingrandimento. Godono della proprietà di invarianza di scala, in altre parole sono “auto somiglianti” , cioè ogni piccola porzione del frattale può essere vista come una riproduzione su scala ridotta dell’intera figura. Un esempio di oggetto frattale a noi familiare e’ il cavolbroccolo romano mostrato in figura 1.

 

Figura 1. Un esempio di oggetto frattale: il cavolbroccolo.

Nel 1623, Galileo Galilei nel suo Saggiatore scriveva: Il libro dell’Universo e’ scritto in lingua matematica e i caratteri sono triangoli, cerchi ed altre figure geometriche, senza i quali mezzi e’ impossibile a intenderne umanamente parole; senza questi e’ un aggirarsi vanamente in un oscuro labirinto.

Che l’Universo fosse scritto in lingua matematica, il grande fisico toscano aveva ragione. Ma sui caratteri no. Basta guardare il mondo che ci circonda per capire che gli oggetti non sono rappresentabili con la semplice geometria euclidea (figura 2).

 

Figura 2. Gli oggetti reali con le forme della geometria classica.

Cio’ spinse il matematico B. Mandelbrot nel 1975 ad osservare che la geometria euclidea e’ incapace di descrivere la natura nella sua complessita’, in quanto si limita a descrivere tutto cio’ che e’ regolare, mentre osservando la natura vediamo che le montagne non sono coni, le nuvole non sono delle sfere, le coste non sono cerchi; si tratta di oggetti geometricamente molto complessi. Da qui nasce la geometria frattale. Una delle proprietà tipica dei frattali, oltre all’auto somiglianza, e’ la loro dimensione non intera che e’ abbastanza inusuale per noi abituati a giocherellare con la geometria Euclidea. Vediamo di che cosa si tratta.

Per prima cosa dobbiamo capire che cosa si intende per dimensione. Aristotele affermava: “..... delle grandezze, quella che ha una dimensione e’ linea, quella che ne ha due e’ superficie, quella che ne ha tre e’ corpo, e al di fuori di questo non si hanno altre grandezze......” . Quindi:

1. Un punto non ha alcuna dimensione: ne’ lunghezza, ne’ larghezza ne’ altezza.

2. Una retta ha una sola dimensione: la lunghezza che si estende fino all’infinito in entrambe le direzioni.

3. Il piano ha due dimensioni: lunghezza e larghezza, e si estende fino all’infinito in entrambe le direzioni.

4. Lo spazio ha tre dimensioni: lunghezza, larghezza e altezza che si estendono fino all’infinito in tutte e tre le direzioni.

Ma c’e’ una definizione matematica di dimensione?

La risposta e’ si. Con un esempio cerchiamo di arrivare all’equazione che ci permette di ricavare questa grandezza.

Supponiamo di avere un cubo come quello mostrato in figura 3, e supponiamo di raddoppiare la lunghezza del suo lato. Così facendo otteniamo 8 copie dell’originale, cioè: 8=2³. Ma il 3 altro non e’ che la dimensione dello spazio. La stessa cosa per esempio e’ vera nel caso di un rettangolo e di una retta.

 

Figura 3. Raddoppiando la lunghezza del lato di un cubo si ottengono 8 copie dell’originale.

 

Quindi in generale abbiamo:

N=S^D

dove N e’ il numero di copie dell’oggetto che otteniamo ingrandendo un suo lato di S volte e D la dimensione dell’oggetto. Se, per esempio, ingrandiamo ogni lato di un rettangolo 5 volte, otteniamo 25 copie dell’originale e quindi la dimensione D e’ quel numero con cui elevando il 5 otteniamo 25, cioè D=2. Adesso siamo pronti per calcolare la dimensione di un oggetto frattale. Allo scopo utilizzeremo il triangolo di Sierpinski che e’ un frattale che si costruisce nel seguente modo. Iniziamo con un triangolo.

Disegniamo le linee che uniscono i punti centrali di ogni lato e rimuoviamo il triangolo che si forma al centro.

All’interno di questo triangolo, abbiamo 3 nuovi triangoli.

Ripetiamo l’operazione precedente per questi 3 triangoli (cioè uniamo tra loro i punti centrali di ogni lato del triangolo e rimuoviamo il triangolo centrale). Il risultato e’ il seguente.

Se ripetiamo l’operazione diverse volte otteniamo il triangolo di Sierpinski.

Calcoliamo, adesso, la dimensione di questo oggetto osservando che raddoppiando la lunghezza del lato del triangolo abbiamo tre copie esatte dell’originale e questo a qualsiasi passo della costruzione.

Quindi, sostituendo questi numeri all’interno dell’equazione N=S^D , otteniamo:

3=2^D

Questa equazione può essere risolta utilizzando il concetto di logaritmo e cioè:

Log(3)=Log(2^D)=Dlog(2)    da cui si ricava    D=Log(3)/Log(2)=1.585

La dimensione del triangolo di Sierpinski e’ data da un numero che sta tra 1 e 2. Cioè questo oggetto geometrico e’ qualche cosa che sta quasi a metà tra una retta e un piano. La geometria frattale non ‘e semplicemente il frutto di una speculazione teorica, ma trova anche interessanti applicazioni nella realtà. Nel corpo umano strutture riconducibili a frattali sono osservabili nelle reti di vasi sanguigni, di fibre nervose e di strutture canalizzate. Il sistema frattale più studiato e' l'albero bronchiale, che trasporta i gas respiratori da e verso i polmoni (figura 4). Nel cuore, le strutture frattali hanno un ruolo vitale nella meccanica della contrazione e nella conduzione dello stimolo elettrico eccitatorio. Una rete frattale di arterie e vene coronarie trasporta sangue da e verso il cuore (figura 5). Recentemente la geometria frattale e’ stata utilizzata anche per spiegare alcune anomalie del flusso sanguigno coronarico, la cui interruzione può causare l'infarto miocardico.

 

Figura 4. La struttura frattale dei bronchi.

 

Figura 5. La struttura frattale del cuore.

Si cerca di applicare la matematica dei frattali anche allo studio dei tumori, in quanto, si e’ scoperto che nell’organismo colpito da tale patologia tendono a formarsi vasi sanguigni che nutrono le cellule tumorali seguendo uno schema frattale (figura 6).

 

Figura 6. La struttura frattale dei vasi sanguigni di un tumore.

Oggi, nonostante la migliorata conoscenza dei meccanismi che regolano i tumori, la maggior parte delle diagnosi ancora si basa sull’ispezione visiva delle immagini radiologiche. Queste immagini, ovviamente vengono interpretate in modo qualitativo da medici che sono stati addestrati a classificare strutture irregolari. Un approccio piu’ riproducibile e quantitativo, da affiancare all’osservazione del medico, puo’ essere quello dell’analisi delle immagini con software adeguati. E qui entra in gioco la geometria frattale che viene utilizzata per misurare l’irregolarita’ delle strutture tumorali. Come gia’ detto, si e’ scoperto che la vascolarizzazione dei tumori, e’ piu’ caotica di quella normale (figura 7). Da esperimenti effettuati, si e’ visto che i vasi sanguigni dei tumori hanno dimensioni intorno ad 1.89, mentre le normali arterie e vene hanno una dimensione frattale di 1.70. La dimensione frattale dei tumori puo’ essere ottenuta usando un processo di crescita statistica conosciuto come percolazione invasiva. La percolazione normalmente, viene associata con il movimento dell’acqua attraverso le fessure del suolo. In termini tecnici, una percolazione invasiva e’ un algoritmo che modella l’espansione di una rete attraverso un mezzo con eterogeneita’ resistive distribuite in modo casuale. La rete (network) risultante si espande sempre nei siti meno resistenti, generando strutture con vuoti e strutture tortuose su larga scala. Nel 1995 alcuni ricercatori hanno dimostrato che la percolazione invasiva riusciva a mimare correttamente la transizione da una normale vascolarizzazione a quella irregolare di un tumore.

 

Figura 7. Immagine di arterie e vene normali A, normali capillari sottocutanei B, vascolarizzazione di un tumore C.

Nella figura 8, vengono riportate alcune fasi della crescita di una percolazione invasiva. I quadratini con diversi colori rappresentano la diversa intensita’ delle eterogeneita’. Il nero corrisponde alla massima intensita’ e viceversa il bianco alla minima. Il punto nero rappresenta la cella iniziale e i vari segmenti la rete percolativa. Il punto iniziale si muove orizzontalmente o verticalmente di un solo passo alla volta e nella cella con minima intensita’ (A). Nella figura B viene riportata la rete percolativa dopo un certo numero di passi. Notare la somiglianza con la vascolarizzazione di un tumore.

 

’Figura 8. Simulazione percolazione invasiva. Per i dettagli vedere testo.

Anche nel mondo vegetale si trovano svariati esempi di strutture frattali: i rami delle piante, le radici di un albero, le felci (figura 13), le nuvole, le ramificazioni di un fulmine (figura 14), i fiocchi di neve (vedi figura 15), e addirittura i raggruppamenti delle galassie nell’universo.

 

Figura 13. Albero e felci frattali.

 

Figura 14. Sulla sinistra e al centro due tipologie di fulmini. Sulla destra un frattale ramificato.

 

Figura 15. Fiocco di neve frattale. Le diverse fasi di costruzione di questo oggetto.

Cerchiamo di approfondire un attimo quest’ultimo concetto.

Se si osserva il cielo stellato, ad un primo sguardo sembra che le stelle ricoprano uniformemente la volta celeste. Ma restando per un po’ al buio l’occhio subito comincia a distinguere una zona del cielo piu’ luminosa e densa di quelle circostanti: si tratta della Via Lattea, la nostra Galassia. Come tutti sapranno, le galassie sono insieme di miliardi di stelle tenute insieme dalla gravita’. Sono un po’ come le cellule del nostro organismo. Queste galassie, a loro volta, formano degli ammassi di galassie che a loro volta sembrano organizzati in superammassi (vedi figura 16). E’ lecito chiedersi, allora, se questo gioco delle matrioske sia presente su scale sempre piu’ grandi.

 

Figura 16. L’universo ripreso dal telescopio Hubble.

Se cosi fosse, questo vorrebbe dire che la materia luminosa nell’universo non sarebbe distribuita in modo uniforme, bensi’ in un alternanza di spazi pieni e di spazi vuoti, cioe’ un universo frattale. Questa tesi, sostenuta oggi da diversi cosmologi, e’ stata avanzata per la prima volta dal professore Luciano Pietronero dell’Universita’ la Sapienza di Roma. Osservando la figura 17, si puo’ notare come la distribuzione delle galassie alterna addensamenti e vuoti a tutte le scale di lunghezza a noi accessibili con gli strumenti che oggi sono a nostra disposizione. Questa e’ precisamente la caratteristica di una struttura frattale.

 

Figura 17. La trama frattale delle galassie

Ma nessuno ci puo’ assicurare che la distribuzione delle galassie non diventi omogenea aumentando il volume dell’universo osservato.La questione dell’omogeneita’ della materia luminosa e’ di cruciale importanza per la cosmologia. Proprio sull’omogeneita’ si basa infatti uno dei principi piu’ importanti della cosmologia attuale: il principio cosmologico.

Di cosa si tratta?

Il modello cosmologico standard, una versione del quale prevede il Big Bang, e’ quello che ad oggi riesce meglio a spiegare l’origine e l’evoluzione dell’universo. Quindi, e’ chiaro, che se la distribuzione della materia si rivelasse frattale a tutte le scale, il modello cosmologico standard andrebbe rivisto completamente. Comunque, la maggior parte degli scienziati sono convinti che le galassie piu’ vicine a noi hanno effettivamente una distribuzione frattale, che pero’ tende all’omogeneita’ man mano che ci si addentra in regioni dell’universo sempre piu’ lontane nello spazio e nel tempo. Insomma, l’universo sarebbe comunque omogeneo su grande scala.

Luciano Pietronero e i suoi colleghi, tuttavia, ritengono che alla base dell’approccio di questi scienziati ci sia una certa riluttanza a mettere in discussione il Principio cosmologico. Puo’ essere utile, allora, tentare di capire come e perche’ si siano formate le strutture luminose che osserviamo. Indicazioni importanti, probabilmente non verranno solo dalle ricerche nell’infinitamente grande, ma anche da quelle nell’infinitamente piccolo, come gli esperimenti con l’LHC (Large Hadron Collider) che sono in corso al CERN di Ginevra. In uno di questi esperimenti si cerchera’ di riprodurre le condizioni iniziali del Big Bang.

Numeri geometrici

 

Possono i numeri avere una forma geometrica?

Anche se e’ chiaro di no, alcuni di essi possono essere rappresentati da punti disposti come figure geometriche regolari. Questi numeri vengono chiamati numeri figurati o numeri poligonali.
I numeri figurati più conosciuti sono i numeri quadrati, cioè i numeri 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121,…….
Essi si chiamano così perché possono essere disposti all’interno di quadrati come quelli riportati sotto.

Gli angoli rossi sono quelli che gli antichi Greci chiamavano “gnomon”. Ogni quadrato e’ formato dal quadrato precedente indicato in blu più lo gnomon. I numeri appartenenti allo gnomon dei numeri quadrati sono: 1, 3, 5, 7, 9, 11,…. Praticamente i numeri dispari.

Da qui discende facilmente che l'ennesimo numero quadrato e’ dato dalla somma del quadrato precedente piu' i numeri dispari consecutivi. Allo stesso modo e’ possibile trasformare in termini matematici quello che abbiamo visto con la rappresentazione geometrica, cioè che e’ vera la seguente formula ricorsiva per i numeri quadrati Q:

Q_k+1=Q_k+2k+1

dove k=0, 1, 2, 3, 4…. e Q₀=0

Il numero di rappresentazioni di un numero n tramite k quadrati, distinguendo il segno e l’ordine, viene indicato con r_k(n); si tratta di una funzione di n chiamata la funzione della somma dei quadrati. Per esempio, consideriamo il numero di modi in cui e’ possibile rappresentare il numero 5 come somma di 2 quadrati:

e quindi r₂(5)=8. Allo stesso modo il numero 4 puo’ essere scritto come somma di tre quadrati come segue:

e quindi r₂(4)=6.

Diversi grandi matematici hanno contribuito a determinare un’espressione analitica di questa funzione. Jacobi ci riusci’ nel 1829 per k=2,4,6, e 8. La soluzione per k=10 e 12, invece, fu trovata da Liouville e in seguito da Eisenstein. Glaisher nel 1907, riusci a sviluppare una tabella di  r_2s(n) per 2s fino a 18. Il grande Ramanujan, estese il risultato di Glaisher fino a 2s=24.

La funzione  r₂(n) a volte indicata come r(n) e’ intimamente connessa al problema del cerchio di Gauss.

Questo problema consiste nel contare, per un cerchio di raggio r, il numero dei punti del reticolo N(r), all’interno dei confini del cerchio (confine incluso) con centro nell’origine (vedi figura 1).

 

Figura 1: Problema del cerchio di Gauss.

L’esatta soluzione di questo problema e’ data dalla formula:

dove la funzione

indica la parte intera del numero n. I primi valori di N(r) per r=0,1,2,3…. sono 1, 5, 13, 29, 49, 81, 113, 149…….

La serie N(r) e’ legata alla funzione della somma di due quadrati r(n) in quanto si puo’ dimostrare che:

In figura 2, viene riportata la rappresentazione della funzione N(r)/r²  in funzione di r. Osservare l’andamento asintotico della funzione dopo aver attraversato una zona per bassi valori di r con grosse oscillazioni.

 

Figura 2: Andamento del rapporto N(r) e il quadrato di r

I numeri 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, ... sono invece i cosiddetti numeri triangolari in quanto possono essere rappresentati tramite triangoli regolari.

Se con T_k indichiamo il k-esimo numero triangolare si può verificare che vale la seguente relazione:

con T₀=0.

Questa relazione ricorsiva può essere espansa per dimostrare che il k-esimo numero triangolare altro non e’ che la somma di tutti numeri da 1 a k.

Poiché la somma dei primi k numeri e’ data da k(k+1)/2 possiamo scrivere che:

Osservare che a partire dai numeri triangolari si possono ottenere i numeri quadrati. E’ facile, infatti, dimostrare che:

Schematicamente questa relazione può essere rappresentata nel seguente modo:

Qui l’n-1_esimo numero triangolare e’ rappresentato dai triangoli bianchi, l’n_simo numero triangolare dal numero di triangoli neri mentre il numero totale dei triangoli e’ l’ennesimo numero quadrato.

Un'altra relazione dimostrata da Conway e Guy nel 1996, lega i numeri triangolari a quelli quadrati.

Si può verificare che essa e’ vera osservando che e’ sempre possibile dividere un quadrato in 8 triangoli a parte un tassello.

Nel 1638, Fermat propose che ogni numero intero positivo, e’ la somma di almeno tre numeri triangolari, quattro numeri quadrati, cinque numeri pentagonali e cosi via.

Egli riportò di avere una dimostrazione, anche se essa non e’ mai stata trovata.

In seguito Gauss provò che il caso dei numeri triangolari era vero e annoto’ l’evento sul suo diario (10 Luglio 1796) con la scritta ormai famosa:
 

Il caso dei numeri quadrati fu dimostrato da Jacobi e Lagrange nel 1772, mentre l’intero teorema e’ stato dimostrato solo nel 1813 da Cauchy.

Allo stesso modo dei numeri triangolari e numeri quadrati e’ possibile costruire numeri pentagonali, esagonali, ettagonali ….. In generale possiamo parlare di numeri poligonali. Questi numeri sono caratterizzati da due parametri: il numero E dei vertici e il numero k del rango (il primo, secondo, terzo etc). Il minimo valore per questi due parametri e’ 3 ed 1 rispettivamente.

Con G(E,k) indichiamo il numero poligonale con E vertici e allo stadio k.

I numeri:

G(3,k) rappresentano i numeri triangolari

G(4,k) i numeri quadrati

G(5,k) i numeri pentagonali

G(6,k) i numeri esagonali

G(7,k) i numeri ettagonali

G(8,k) i numeri ottagonali

e cosi via. I numeri poligonali sono numeri i cui punti che li rappresentano possono essere disposti all’interno di poligoni regolari. Allo stadio k=1 ogni numero poligonale e’ costituito da un solo punto, cioè G(E,1)=1. Per k maggiore o uguale a 2   il numero poligonale appartenente alla famiglia G(E,k) evolve da quello precedente G(E,k-1) mettendo insieme una “catena” aperta di nuovi punti ai k-2 lati del vecchio pattern cosicché i vertici andranno a formare un nuovo poligono con esattamente k punti su ognuno dei suoi lati.

Nei seguenti esempi in blu vengono riportati i precedenti pattern e in rosso le catene aperte dei nuovi punti.

Esempio di numeri pentagonali.

Esempio di numeri esagonali.

Da queste figure si può facilmente dimostrare che: