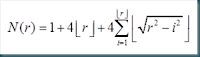In questo nuovo post parleremo di frattali. Si tratta di oggetti geometrici che presentano una struttura complessa e dettagliata ad ogni livello di ingrandimento. Godono della proprietà di invarianza di scala, in altre parole sono “auto somiglianti” , cioè ogni piccola porzione del frattale può essere vista come una riproduzione su scala ridotta dell’intera figura. Un esempio di oggetto frattale a noi familiare e’ il cavolbroccolo romano mostrato in figura 1.
Figura 1. Un esempio di oggetto frattale: il cavolbroccolo.
Nel 1623, Galileo Galilei nel suo Saggiatore scriveva: Il libro dell’Universo e’ scritto in lingua matematica e i caratteri sono triangoli, cerchi ed altre figure geometriche, senza i quali mezzi e’ impossibile a intenderne umanamente parole; senza questi e’ un aggirarsi vanamente in un oscuro labirinto.
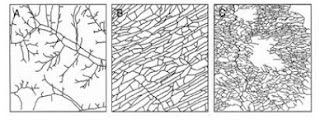
Che l’Universo fosse scritto in lingua matematica, il grande fisico toscano aveva ragione. Ma sui caratteri no. Basta guardare il mondo che ci circonda per capire che gli oggetti non sono rappresentabili con la semplice geometria euclidea (figura 2).
Figura 2. Gli oggetti reali con le forme della geometria classica.
Cio’ spinse il matematico B. Mandelbrot nel 1975 ad osservare che la geometria euclidea e’ incapace di descrivere la natura nella sua complessita’, in quanto si limita a descrivere tutto cio’ che e’ regolare, mentre osservando la natura vediamo che le montagne non sono coni, le nuvole non sono delle sfere, le coste non sono cerchi; si tratta di oggetti geometricamente molto complessi. Da qui nasce la geometria frattale. Una delle proprietà tipica dei frattali, oltre all’auto somiglianza, e’ la loro dimensione non intera che e’ abbastanza inusuale per noi abituati a giocherellare con la geometria Euclidea. Vediamo di che cosa si tratta.
Per prima cosa dobbiamo capire che cosa si intende per dimensione. Aristotele affermava: “..... delle grandezze, quella che ha una dimensione e’ linea, quella che ne ha due e’ superficie, quella che ne ha tre e’ corpo, e al di fuori di questo non si hanno altre grandezze......” . Quindi:
1. Un punto non ha alcuna dimensione: ne’ lunghezza, ne’ larghezza ne’ altezza.
2. Una retta ha una sola dimensione: la lunghezza che si estende fino all’infinito in entrambe le direzioni.
3. Il piano ha due dimensioni: lunghezza e larghezza, e si estende fino all’infinito in entrambe le direzioni.
4. Lo spazio ha tre dimensioni: lunghezza, larghezza e altezza che si estendono fino all’infinito in tutte e tre le direzioni.
Ma c’e’ una definizione matematica di dimensione?
La risposta e’ si. Con un esempio cerchiamo di arrivare all’equazione che ci permette di ricavare questa grandezza.
Supponiamo di avere un cubo come quello mostrato in figura 3, e supponiamo di raddoppiare la lunghezza del suo lato. Così facendo otteniamo 8 copie dell’originale, cioè: 8=23. Ma il 3 altro non e’ che la dimensione dello spazio. La stessa cosa per esempio e’ vera nel caso di un rettangolo e di una retta.
Figura 3. Raddoppiando la lunghezza del lato di un cubo si ottengono 8 copie dell’originale.
Quindi in generale abbiamo:
N=SD
dove N e’ il numero di copie dell’oggetto che otteniamo ingrandendo un suo lato di S volte e D la dimensione dell’oggetto. Se, per esempio, ingrandiamo ogni lato di un rettangolo 5 volte, otteniamo 25 copie dell’originale e quindi la dimensione D e’ quel numero con cui elevando il 5 otteniamo 25, cioè D=2. Adesso siamo pronti per calcolare la dimensione di un oggetto frattale. Allo scopo utilizzeremo il triangolo di Sierpinski che e’ un frattale che si costruisce nel seguente modo. Iniziamo con un triangolo.
Disegniamo le linee che uniscono i punti centrali di ogni lato e rimuoviamo il triangolo che si forma al centro.
All’interno di questo triangolo, abbiamo 3 nuovi triangoli.
Ripetiamo l’operazione precedente per questi 3 triangoli (cioè uniamo tra loro i punti centrali di ogni lato del triangolo e rimuoviamo il triangolo centrale). Il risultato e’ il seguente.
Se ripetiamo l’operazione diverse volte otteniamo il triangolo di Sierpinski.
Calcoliamo, adesso, la dimensione di questo oggetto osservando che raddoppiando la lunghezza del lato del triangolo abbiamo tre copie esatte dell’originale e questo a qualsiasi passo della costruzione.
Quindi, sostituendo questi numeri all’interno dell’equazione N=SD , otteniamo:
3=2D
Questa equazione può essere risolta utilizzando il concetto di logaritmo e cioè:
Log(3)=Log(2D)=Dlog(2) da cui si ricava D=Log(3)/Log(2)=1.585
La dimensione del triangolo di Sierpinski e’ data da un numero che sta tra 1 e 2. Cioè questo oggetto geometrico e’ qualche cosa che sta quasi a metà tra una retta e un piano. La geometria frattale non ‘e semplicemente il frutto di una speculazione teorica, ma trova anche interessanti applicazioni nella realtà. Nel corpo umano strutture riconducibili a frattali sono osservabili nelle reti di vasi sanguigni, di fibre nervose e di strutture canalizzate. Il sistema frattale più studiato e' l'albero bronchiale, che trasporta i gas respiratori da e verso i polmoni (figura 4). Nel cuore, le strutture frattali hanno un ruolo vitale nella meccanica della contrazione e nella conduzione dello stimolo elettrico eccitatorio. Una rete frattale di arterie e vene coronarie trasporta sangue da e verso il cuore (figura 5). Recentemente la geometria frattale e’ stata utilizzata anche per spiegare alcune anomalie del flusso sanguigno coronarico, la cui interruzione può causare l'infarto miocardico.
Figura 4. La struttura frattale dei bronchi.
Figura 5. La struttura frattale del cuore.
Si cerca di applicare la matematica dei frattali anche allo studio dei tumori, in quanto, si e’ scoperto che nell’organismo colpito da tale patologia tendono a formarsi vasi sanguigni che nutrono le cellule tumorali seguendo uno schema frattale (figura 6).
Figura 6. La struttura frattale dei vasi sanguigni di un tumore.
Oggi, nonostante la migliorata conoscenza dei meccanismi che regolano i tumori, la maggior parte delle diagnosi ancora si basa sull’ispezione visiva delle immagini radiologiche. Queste immagini, ovviamente vengono interpretate in modo qualitativo da medici che sono stati addestrati a classificare strutture irregolari. Un approccio piu’ riproducibile e quantitativo, da affiancare all’osservazione del medico, puo’ essere quello dell’analisi delle immagini con software adeguati. E qui entra in gioco la geometria frattale che viene utilizzata per misurare l’irregolarita’ delle strutture tumorali. Come gia’ detto, si e’ scoperto che la vascolarizzazione dei tumori, e’ piu’ caotica di quella normale (figura 7). Da esperimenti effettuati, si e’ visto che i vasi sanguigni dei tumori hanno dimensioni intorno ad 1.89, mentre le normali arterie e vene hanno una dimensione frattale di 1.70. La dimensione frattale dei tumori puo’ essere ottenuta usando un processo di crescita statistica conosciuto come percolazione invasiva. La percolazione normalmente, viene associata con il movimento dell’acqua attraverso le fessure del suolo. In termini tecnici, una percolazione invasiva e’ un algoritmo che modella l’espansione di una rete attraverso un mezzo con eterogeneita’ resistive distribuite in modo casuale. La rete (network) risultante si espande sempre nei siti meno resistenti, generando strutture con vuoti e strutture tortuose su larga scala. Nel 1995 alcuni ricercatori hanno dimostrato che la percolazione invasiva riusciva a mimare correttamente la transizione da una normale vascolarizzazione a quella irregolare di un tumore.
Figura 7. Immagine di arterie e vene normali A, normali capillari sottocutanei B, vascolarizzazione di un tumore C.
Nella figura 8, vengono riportate alcune fasi della crescita di una percolazione invasiva. I quadratini con diversi colori rappresentano la diversa intensita’ delle eterogeneita’. Il nero corrisponde alla massima intensita’ e viceversa il bianco alla minima. Il punto nero rappresenta la cella iniziale e i vari segmenti la rete percolativa. Il punto iniziale si muove orizzontalmente o verticalmente di un solo passo alla volta e nella cella con minima intensita’ (A). Nella figura B viene riportata la rete percolativa dopo un certo numero di passi. Notare la somiglianza con la vascolarizzazione di un tumore.
’Figura 8. Simulazione percolazione invasiva. Per i dettagli vedere testo.
Anche nel mondo vegetale si trovano svariati esempi di strutture frattali: i rami delle piante, le radici di un albero, le felci (figura 13), le nuvole, le ramificazioni di un fulmine (figura 14), i fiocchi di neve (vedi figura 15), e addirittura i raggruppamenti delle galassie nell’universo.
Figura 13. Albero e felci frattali.
Figura 14. Sulla sinistra e al centro due tipologie di fulmini. Sulla destra un frattale ramificato.
Figura 15. Fiocco di neve frattale. Le diverse fasi di costruzione di questo oggetto.
Cerchiamo di approfondire un attimo quest’ultimo concetto.
Se si osserva il cielo stellato, ad un primo sguardo sembra che le stelle ricoprano uniformemente la volta celeste. Ma restando per un po’ al buio l’occhio subito comincia a distinguere una zona del cielo piu’ luminosa e densa di quelle circostanti: si tratta della Via Lattea, la nostra Galassia. Come tutti sapranno, le galassie sono insieme di miliardi di stelle tenute insieme dalla gravita’. Sono un po’ come le cellule del nostro organismo. Queste galassie, a loro volta, formano degli ammassi di galassie che a loro volta sembrano organizzati in superammassi (vedi figura 16). E’ lecito chiedersi, allora, se questo gioco delle matrioske sia presente su scale sempre piu’ grandi.
Figura 16. L’universo ripreso dal telescopio Hubble.
Se cosi fosse, questo vorrebbe dire che la materia luminosa nell’universo non sarebbe distribuita in modo uniforme, bensi’ in un alternanza di spazi pieni e di spazi vuoti, cioe’ un universo frattale. Questa tesi, sostenuta oggi da diversi cosmologi, e’ stata avanzata per la prima volta dal professore Luciano Pietronero dell’Universita’ la Sapienza di Roma. Osservando la figura 17, si puo’ notare come la distribuzione delle galassie alterna addensamenti e vuoti a tutte le scale di lunghezza a noi accessibili con gli strumenti che oggi sono a nostra disposizione. Questa e’ precisamente la caratteristica di una struttura frattale.
Figura 17. La trama frattale delle galassie
Ma nessuno ci puo’ assicurare che la distribuzione delle galassie non diventi omogenea aumentando il volume dell’universo osservato.La questione dell’omogeneita’ della materia luminosa e’ di cruciale importanza per la cosmologia. Proprio sull’omogeneita’ si basa infatti uno dei principi piu’ importanti della cosmologia attuale: il principio cosmologico.
Di cosa si tratta?
Il modello cosmologico standard, una versione del quale prevede il Big Bang, e’ quello che ad oggi riesce meglio a spiegare l’origine e l’evoluzione dell’universo. Quindi, e’ chiaro, che se la distribuzione della materia si rivelasse frattale a tutte le scale, il modello cosmologico standard andrebbe rivisto completamente. Comunque, la maggior parte degli scienziati sono convinti che le galassie piu’ vicine a noi hanno effettivamente una distribuzione frattale, che pero’ tende all’omogeneita’ man mano che ci si addentra in regioni dell’universo sempre piu’ lontane nello spazio e nel tempo. Insomma, l’universo sarebbe comunque omogeneo su grande scala.
Luciano Pietronero e i suoi colleghi, tuttavia, ritengono che alla base dell’approccio di questi scienziati ci sia una certa riluttanza a mettere in discussione il Principio cosmologico. Puo’ essere utile, allora, tentare di capire come e perche’ si siano formate le strutture luminose che osserviamo. Indicazioni importanti, probabilmente non verranno solo dalle ricerche nell’infinitamente grande, ma anche da quelle nell’infinitamente piccolo, come gli esperimenti con l’LHC (Large Hadron Collider) che sono in corso al CERN di Ginevra. In uno di questi esperimenti si cerchera’ di riprodurre le condizioni iniziali del Big Bang.