Cucinare una pizza: questione di fisica e non solo

Cuocere una pizza puo’ apparire un processo molto semplice a chi come noi e’ abituato a vedere questo disco di pasta uscire velocemente da un forno ed essere servito a tavola per la gioia di chi attende. Eppure in questo semplice processo c’e’ tanta fisica che tre studiosi hanno provato ad analizzare in un loro articolo apparso su arxiv nel mese di Giugno. Il loro obiettivo e’ stato quello di analizzare e confrontare la cottura di una pizza in un forno a legna e in uno elettrico. I principi e le equazioni chiamate in causa sono quelle della termodinamica, una branca della fisica.

Quando si parla di pizza, tutti pensano a Napoli anche se l’origine della pizza è molto piu’ antica. Nel Neolitico tra la Cina e le Americhe c’era gia’ l’abitudine di preparare delle focacce non lievitate fatte con farina di grano tenero (farro, orzo) che venivano poi cotte su pietre riscaldate. La parola pizza compare per la prima volta su una pergamena latina dove viene riportata una lista di donazioni fatte da un proprietario terriero al vescovo di Gaeta. Il documento datato al 996 d.C. stabiliva il dono di 12 pizze ogni Natale e Pasqua. La pizza comunque come la conosciamo oggi di sicuro e’ un invenzione dei napoletani, che aggiunsero gli ingredienti universalmente associato oggi alla pizza: pomodoro e mozzarella. I napoletani iniziarono ad usare il pomodoro dopo che Colombo ritorno’ dalle Americhe. Esso appare per la prima volta in un libro di cucina “Cuoco galante” del 1819, scritto dal cuoco Vincenzo Corrado. La mozzarella invece viene citata per la prima volta nel libro di ricette “Opera” del 1570 a cura di Bartolomeo Scappi. Diversi documenti dimostrano che fino al 18 secolo la pizza napoletana era un semplice disco di pasta cotto o fritto, con sopra lardo, formaggio pecorino, olive, sale o piccoli pesci chiamati cecinielli. Durante il 19 secolo ci furono fino a 200 pizzaioli sparsi per i vicoletti di Napoli a vendere le loro pizze cotte o fritte con sopra pomodoro e basilico. Nel 1889, dopo l’unificazione dell’Italia, il pizzaiolo Raffaele Esposito decise di fare un dono alla regina di Italia aggiungendo al pomodoro e al basilico, la mozzarella. La combinazione dei tre colori bianco, rosso e verde simboleggiava la bandiera italiana e da allora in poi questa pizza e’ venne chiamata Pizza Margherita. Raffaele certamente non poteva pensare che un semplice impasto potesse diventare uno degli oggetti più famosi al mondo. Oggi in Italia esistono diversi tipi di pizza a seconda della regione in cui viene preparata. Dalla pizza margherita, marinara e calzone della regione campana alla pizza di sfrigoli dell’abruzzo o alla sfinciuni siciliana solo per citarne alcune. Veniamo adesso alla studio vero e proprio. Quale e’ il segreto di una buona pizza? Come molti pizzaioli riportano, il forno a legno dovrebbe essere superiore a quello elettrico. La temperatura tipica per una pizza alla romana e’ tra 325-330 gradi centigradi mentre per quella napoletana e’ intorno ai 400 gradi. Con queste temperature una pizza è pronta in circa due minuti e un minuto rispettivamente. Assumendo che in un forno possono andare due pizze in contemporanea, in un ora e’ possibile fare tra le 50 e le 60 pizze romane. Nelle ore di picco, comunque i pizzaioli sono abituati ad alzare la temperatura del forno, arrivando anche a 390 gradi per ridurre cosi il tempo di cottura che passa da due minuti a circa 50 secondi e servendo cosi più clienti. Questa operazione quasi innocua, in effetti altera la qualità della pizza in quanto il fondo e la crosta vengono bruciate e il pomodoro non è cotto abbastanza. Poiché non è sempre possibile trovare una pizzeria con il forno a legna, e’ interessante analizzare i possibili vantaggi del forno a legna rispetto a quello elettrico e se c’è la possibilità di migliorare le prestazioni di quest’ultimo per fare una pizza decente. Iniziamo col richiamare alcune dei concetti di base sulla trasmissione del calore. Quando si parla di calore si ha in mente l’energia di un sistema associata al moto caotico degli atomi, molecole o altre particelle di cui e’ composto. Comunque va precisato che il calore come il lavoro non e’ una variabile di stato di un sistema in quanto dipende da come esso ha raggiunto il suo stato, cioe’ dipende dallo stato iniziale, quello finale e dal modo in cui tale variazione e’ stata compiuta. Come il lavoro, il calore e’ un modo conveniente per descrivere un trasferimento di energia. La quantita’ di calore necessaria ad aumentare la temperatura di una massa unitaria di un materiale di un grado Kelvin e’ chiamata calore specifico del materiale:

c=dQ/M*dT

Qui M e’ la massa del sistema e dQ e’ la quantita’ di calore richiesto per far variare la temperatura dT. Il calore specifico e’ misurato in J/(Kg*K).

In caso di contatto tra due sistemi con due temperature diverse, il calore fluira’ da quello piu’ caldo a quello piu’ freddo. Il flusso di calore q e’ la quantita’ di calore dQ che passa attraverso un’ area S per unita’ di tempo dt e nella direzione in cui cambia la temperatura:

q=dQ/(S*dt)

Nel caso piu’ semplice di un sistema omogeneo, combinando le due equazioni precedenti otteniamo:

q=(c*M*dT)/(S*dt)

Ricordando adesso la definizione di densita’ di materia rho=M/V=M/(S*dx) otteniamo:

q=c*rho*dx*dT/dt=c*rho*((dx)²/dt)*(dT/dx)=-k*dT/dx

dove k e’ la conducibilita’ termica e il termine dx²/dt e’ la diffusivita’ termica.

Questa equazione e’ conosciuta con il nome di legge di Fourier ed e’ valida per piccole variazioni di temperatura. Vediamo adesso come il calore penetra in un mezzo dalla superficie di contatto. Rifacendoci all’immagine precedente assumiamo che durante il tempo t la temperatura nel piccolo cilindro di lunghezza L e sezione S sia cambiata di un dT. Utilizzando la legge di Fourier e sostituendo dx con L otteniamo:

c*rho*L*(dT/t)=k*(dT/L)

Risolvendo rispetto ad L si ha:

L=((k*t)/(c*rho))^1/2 =(csi*t)^1/2

cioe’ il fronte di temperatura entra nel mezzo come la radice quadrata del tempo t. Il parametro csi e’ chiamato diffusivita’ termica. Ovviamente l’approccio semplicistico utilizzato ha portato ad un risultato non preciso in quanto l’equazione di Fourier richiede la soluzione di equazioni differenziali. Comunque la differenza tra la soluzione trovata e quella reale sta solo in una costante pi greco:

L=(pi*csi*t)^1/2

Torniamo adesso ai due sistemi in contatto tra loro. Il primo con parametri k₁, c₁, rho₁ e temperatura T₁ e il secondo con parametri k₂, c₂, rho₂ e T₂. Indichiamo con T_o la temperatura all’interfaccia tra i due sistemi. Come detto precedentemente il calore fluisce dal corpo piu’ caldo a quello piu’ freddo, portando cosi la temperatura dei due mezzi alla temperatura di interfaccia T_o:

k₁*((T₁-T_o)/L₁)=k₂*(T_o-T₂)/L₂ (*)

cioe’

k₁*((T₁-T_o)/(pi*csi₁*t)^1/2)=k₂*((T_o-T₂)/(pi*csi₂*t)^1/2)

Risolvendo rispetto a T_o otteniamo

T_o=(T₁+n₂₁*T₂)/(1+n₂₁)

dove n₂₁=(k₂/k₁)*(csi₁/csi₂)^1/2

Notiamo che T_o non dipende dal tempo e quindi rimane costante durante il processo di trasferimento di calore. Nel caso di mezzi uguali con diverse temperature si ottiene

T_o=(T₁+T₂)/2

Cioe’ la temperatura all’interfaccia e’ semplicemente il valore medio delle due temperature. Siamo adesso pronti per passare allo studio del forno a legna. Iniziamo col calcolare la temperatura all’interfaccia tra il fondo della pizza e i mattoni del forno. I parametri necessari vengono riportati in questa tabella.

Assumendo che la temperatura iniziale dell’impasto sia di 20 gradi (T_i=20 C) e che la temperatura all’interno del forno di una pizzeria romana sia di 330 gradi (T_r=330 C) possiamo calcolare la temperatura all’interfaccia pizza- mattoni del forno:

T_ir=(T_r+n₂₁*T_i)/(1+n₂₁)=(330+0.65*20)/1.65=208 C

Con queste temperature mediamente una pizza romana e’ pronta in circa 2 minuti. Ripetiamo adesso lo stesso calcolo per il forno elettrico la cui superficie dove viene poggiata la pizza e’ fatta di acciaio. Questa volta il coefficiente n₂₁ sara’ 0.1 per cui la temperatura all’interfaccia pizza – superficie forno sara’:

T_ir=(330+0.1*20)/1.1=300 C

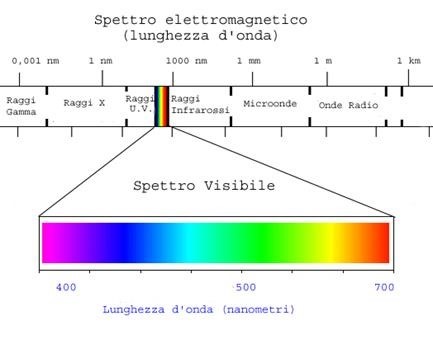
Effettivamente la temperatura all’interfaccia e’ alta e questa determinera’ le classiche bruciature che tutti noi almeno una volta abbiamo visto sul fondo di una pizza. Nel caso della pizza napoletana questa temperatura sara’ ancora piu’ alta essendo la temperatura tipica del forno a legna di circa 400-450 gradi. A quale temperatura allora, nel caso di una pizza romana, dovrebbe essere impostato il forno elettrico per avere sul fondo della pizza la stessa temperatura di un forno a legna? Basta imporre nell’ultima equazione T_ir a 208 gradi e ricavare T_r. Con semplici passaggi si ottiene 230 gradi, una temperatura decisamente piu’ bassa dei 330 gradi del forno a legna. Se fosse tutto qui, allora con un semplice aggiustamento di temperatura la pizza cotta col forno elettrico potrebbe essere equiparabile a quella del forno a legna. Poiche’ e’ ben noto a tutti che questo non e’ vero vuol dire che c’e’ qualche altra cosa che non abbiamo considerato. Ma cosa? I possibili modi di trasmissione del calore. Fin qui abbiamo considerato solo il meccanismo della conduzione. Ma ci deve essere almeno un altro modo. Il sole non e’ in contatto con noi, eppure il suo calore arriva a noi. Come? Grazie alla radiazione termica, cioe’ ai raggi infrarossi. L’energia termica che arriva su un cm2 di superficie per secondo e’ data dalla cosiddetta legge di Stefan-Boltzmann:

I=sigma*T⁴

dove la costante sigma vale 5.67E-8 W/(m²K⁴). L’intensita’ I e’ misurata in W/m² e la temperatura in gradi Kelvin. Poiche’ i forni a legna hanno la volta a doppia corona riempita con sabbia, la temperatura al suo interno rimane costante e cioe’ T_r=330 C=603 K essendo T(K)=273+T(C) la relazione per passare da gradi centigradi a quelli Kelvin. Essendo tutte le parti del forno alla stessa temperatura questo significa che esso e’ pieno di radiazione infrarossa che investe la pizza da tutte le parti. Grazie alla legge di S-B possiamo calcolare questa quantita’:

I=5.67E-8*603⁴ =7.5 kW/m²

cioe’ ogni secondo su un cm² della pizza arrivano circa 0.75 joule di radiazione infrarossa. Va notato comunque che anche la pizza allo stesso tempo emette una radiazione data da I=sigma*(T_pizza)⁴. Quanto vale T_pizza? Poiche’ la maggior parte del tempo di cottura richiesto vien speso per far evaporare l’acqua dall’impasto possiamo assumere che la temperatura della pizza T_pizza sia di 100 gradi, cioe’ 373 gradi Kelvin che risulta in una radiazione termica di circa 1.1 kW/m². Circa il 15% della radiazione ricevuta dalla pizza viene riemessa nel forno. Per il forno elettrico nonostante la temperatura sia piu’ bassa (230 C) la corrispondente energia termica incidente su 1 cm² e’ piu’ del doppio di quella del forno a legna:

I=5.67E-8*(503)⁴=3.6 kW/m²

mentre quella emessa dalla pizza rimane la stessa di prima. Calcoliamo adesso la quantita’ di calore che arriva per cm2 sul fondo della pizza grazie alla conduzione. Possiamo farlo utilizzando l’equazione (*):

q(t)=k*(T₁-T_o)/(pi*csi*t)^1/2

dove T₁ e’ la temperatura del forno. Contrariamente alla legge di Stefen-Boltzmann il trasferimento di calore per conduzione dipende dal tempo t. Quindi la quantita’ di calore trasferita ad 1 cm2 di pizza in un tempo di cottura t_c e’ dato da:

Q(t_c)=2*k*(T₁-T_o)*(t_c/(pi*csi))^1/2

che sommata a quella per irraggiamento ci da’:

Q_tot(t_c)=sigma*(T₁⁴-T_e⁴)*t_c+2*k*(T₁-T_o)*(t_c/(pi*csi))^1/2

dove T_e e’ la temperatura di evaporazione dell’acqua dall’impasto della pizza (100 gradi) e T₁ la temperatura del forno. Per poter ricavare il tempo di cottura t_c c’e’ bisogno di determinare la quantita’ totale di calore che arriva sulla pizza per cm². Per fare questo dobbiamo tener presente che come detto in precedenza Q_tot serve per portate l’impasto dalla temperatura di 20 gradi fino a 100 gradi che secondo la legge di Fourier e’ dato da:

Q=c*rho*d*(100-20)=80*c*rho*d

dove c e rho sono il calore specifico e la densita’ dell’impasto e d lo spessore della pizza. Ancora non abbiamo finito. Durante la cottura c’e’ l’evaporazione dell’acqua dall’impasto come anche dal pomodoro, mozzarella e gli altri ingredienti utilizzati e quindi possiamo scrivere:

Q’=a*c_a*rho’*d

dove a e’ la frazione di massa dell’acqua evaporata, rho’ la densita’ dell’acqua e c_a il calore latente di evaporazione dell’acqua. Q+Q’ e’ la quantita’ di calore per unita’ di area richiesta per portare l’acqua all’ebollizione e poi in fase vapore. Se forniamo calore ad un liquido esso aumenta la sua temperatura fino al momento in cui non raggiunge il suo punto di ebollizione. Durante il passaggio di stato la temperatura del liquido resta invece invariata nonostante l'apporto di calore. Il calore fornito non viene utilizzato per aumentare l'energia cinetica delle particelle, ma si trasforma in un aumento di energia potenziale delle particelle gassose.

Tale calore, assorbito dal sistema senza produrre un aumento di temperatura, è noto come calore latente.

Dall’equazione:

Q+Q’=Q_tot

possiamo ricavare t_c, il tempo di cottura. Per fare questo pero’ bisogna conoscere la quantita’ di acqua che e’ evaporata durante la cottura della pizza. Una buona assunzione e’ un 20% di perdita di acqua cioe’ a=0.2. Inserendo tutti i valori riportati sino ad ora si ottiene finalmente il tempo di cottura in forno a legna per una pizza romana. Questo risulta essere di 125 secondi. Per il forno elettrico un calcolo analogo porta ad un tempo ottimale di cottura di circa 170 secondi. Effettivamente per una pizza romana i tempi di cottura con un forno a legna si aggirano intorno ai 2 minuti come effettivamente riportato dai pizzaioli di questa citta’. Con questa equazione possiamo anche calcolare quanto tempo e’ necessario per la cottura di una pizza in un forno a legna se la temperatura del forno e’ quella usata dai napoletani e cioe’ di circa 400. In questa caso ci sarebbe una riduzione dei tempi di cottura con un aumento della produttivita’ di circa il 50% (il tempo di cottura si aggira intorno a 82 secondi). Questa la fisica. Interviene poi l’esperienza del pizzaiolo con un magico trucco. Quando sulla pizza ci sono elementi con un alto contenuto di acqua come uova, alici, vegetali il pizzaiolo, una volta verificato che il fondo della pizza e’ cotto la prende con la pala in legno o alluminio e la tiene sollevata dai mattoni del forno per circa 30 secondi. In questo modo si espone la superficie della pizza alla sola radiazione termica. Si evita cosi la bruciatura del fondo della pizza e si ottiene la corretta cottura della superficie. Come spesso si fa in fisica, allo scopo di ottenere dei buoni risultati senza complicare eccessivamente il modello, e’ stato trascurato il terzo modo di trasferimento del calore, quello per convezione visto che il suo effetto e’ trascurabile.

Nonostante tutti gli sforzi tecnologici da parte dei costruttori di forni elettrici (utilizzazione di materiale ceramico come fondo invece dell’acciaio, rotazione della pizza durante la cottura, forni a convezione per simulare il movimento dei gas all’interno di un forno a legna) il forno a legna rimane lo strumento ideale per cuocere una pizza. L’odore del pomodoro e della mozzarella che cuociono misto all’odore della legna che brucia e’ un qualche cosa di unico ed eccezionale che mai nessuna tecnologia potra’ sostituire. Buona pizza a tutti.

La vastita’ del cosmo

Oggi grazie al progresso tecnologico, gli astronomi riescono ad andare indietro nel tempo ed osservare l’universo subito dopo il Big Bang (circa 380000 anni dopo). Questo perche’ la velocita’ della luce e’ costante e quindi un raggio luminoso di una stella per arrivare a noi impieghera’ un tempo tanto maggiore quanto piu’ e’ lontana da noi. Questo sembra indicare che l’intero universo sia alla portata dei nostri telescopi. Essendo l’eta’ del nostro Universo di 13.7 miliardi di anni questo significa che gli astronomi possono orientare i loro telescopi in ogni direzione dello spazio ottenendo cosi una sfera visibile di 13.7 miliardi di anni luce e con la terra al suo centro. Ma noi sappiamo che l’universo si sta espandendo e questo fa si che il diametro dell’universo osservabile sia di ben 92 miliardi di anni luce. Ma come e’ possibile?

Per rispondere dobbiamo partire dalla ben nota legge di Hubble. Questa stabilisce che la velocita' di recessione delle Galassie e' proporzionale alla loro distanza cioe':

Vr=H*d

dove la costante di proporzionalita' H oggi e' chiamata costante di Hubble e le cui dimensioni sono quelle di un inverso del tempo. La migliore stima conosciuta oggi per questa costante e' :

~ 67 (Km/s)/Mpc

dove Mpc (Mega parsec) e' una misura di distanza equivalente a 3*10²² metri. Volendo esprimere la costante di Hubble in 1/sec abbiamo:

H=(67*1000)/(3*10²²)=67/3*10³*10^-22=67/3*10^-19=22.3*10^-19 1/sec

Detto cio' dobbiamo fare una precisazione: nella relativita' di Einstein non sono le galassie ad allontanarsi tra loro ma lo spazio tra di esse a dilatarsi (da ogni punto del cosmo "emerge' di continuo nuovo spazio). Possiamo fare l'esempio classico del palloncino con sopra incollate delle monetine. Quest'ultime rappresentano le nostre galassie e la superficie del palloncino il tessuto spazio-temporale del cosmo. Se gonfiamo il palloncino (espansione dell'universo) la sua superficie aumenta e le monetine si allontaneranno sempre di piu' senza pero' che le loro dimensioni cambino. Questo e' quello che succede alle galassie "incastonate" nella trama dello spazio tempo. Quest'ultimo si dilata, le galassie si allontanano ma le loro dimensioni rimangono inalterate. Questa dilatazione del cosmo implica alcuni problemi con la misura di distanza. Se l'universo fosse statico allora due galassie qualsiasi sarebbero ad una certa distanza immutabile nel tempo essendo tutto fermo. In questo caso supponendo che una delle galassie sia la nostra, la seconda galassia sarebbe ad una certa distanza da noi e la luce emessa da ques'ultima arriverebbe a noi dopo un tempo dato dalla distanza diviso la velocita' della luce (massima velocita' possibile per gli oggetti all'interno dell'universo). Quando la luce ci raggiunge la galassia che l'ha emessa starebbe sempre li alla stessa distanza di quando la luce e' partita. Ma noi sappiamo che l'universo non e' statico ma e' in espansione e in questo momento sta addirittura accelerando. Questo significa che quando una stella o una galassia emette la luce si troveranno ad una certa distanza chiamiamola d₁ da noi. Una volta che I fotoni partono alla volta della nostra terra, il corpo che ha emesso la luce trovandosi "incastrato" nella trama dello spazio tempo subira' una dilatazione che lo portera' ad allontanarsi dalla terra seguendo la legge di Hubble. Quando i fotoni arriveranno sulla Terra il corpo che l'ha emessi sara' adesso ad una distanza d₁+d₂ dove d₂ e' la distanza coperta dall'oggetto nel tempo in cui i fotoni sono arrivati sulla terra. Questa distanza d_c=d₁+d₂ viene chiamata distanza comovente che e' ben diversa dal concetto di distanza che abbiamo noi quando misuriamo per esempio la lunghezza di un'asta con lo spazio tempo che fa da spettatore. Supponiamo adesso che una stella emetta un fotone da una distanza di 13 miliardi di anni luce. Questo vuol dire che il fotone arrivera' sulla terra dopo 13 miliardi di anni. Ma durante tutti questi anni la stella ha continuato ad allontanarsi da noi a causa dell'espansione dell'universo e quindi si trovera' ben piu' lontana dei 13 miliardi di anni luce iniziali. Ma a che velocita' si espande lo spazio tempo? C'e' un limite cosi come per gli oggetti nell'universo? La risposta e' no. Lo spazio tempo non e' soggetto al vincolo della velocita' della luce. Partendo dalla legge di Hubble possiamo calcolare a quale distanza dalla Terra una galassia "incastonata" nello spazio tempo raggiunge la velocita' della luce. Partendo dalla legge di Hubble e sostituendo c a Vr:

c=H*d

d=c/H=13.4 miliardi di anni luce

Per distanze superiori a questa chiamata raggio di Hubble le galassie si allontanano radialmente dalla terra ad una velocita' maggiore della luce. Questo raggio ci dice che per tutto quello che si trova al di la' di esso non potremo piu' avere nessuna informazione. Questo limite e' anche chiamato orizzonte degli eventi. In cosmologia esiste anche un' altra definizione molto importante che va sotto il nome di "universo osservabile". ovvero quella regione del cosmo da cui abbiamo potuto ricevere anche in passato un segnale luminoso. Come gia' detto se l'universo fosse statico tale regione si estenderebbe per 13.7 miliari di anni luce perche' questa sarebbe la distanza percorsa dalla luce dal Big Bang ad oggi. Ma l'universo nel frattempo si e' dilatato e secondo le equazioni differenziali della relativita' generale di Einstein, il raggio di tale regione sarebbe di ~46 miliardi di anni luce. Questa equazione differenziale lega la distanza comovente al redshift z e non e' risolvibile in forma chiusa ma solo analiticamente. La forma matematica della distanza comovente in funzione del redshift e' una sigmoide che parte da zero e tende a saturare al valore di ~46 miliardi anni luce per valori di z intorno a 1000. Quindi il diametro dell'universo osservabile e' di circa 90 miliardi di anni luce. Chiudiamo con un esempio pratico. Consideriamo la galassia Z8-GND 5296 con un parametro di redshift z di 7.5 (misurato dal telescopio Hubble alcuni anni fa). Grazie alla relazione che lega la velocita' radiale di un corpo con lo spostamento della lunghezza d'onda della radiazione ricevuta rispetto a quella emessa (parametro redshift z):

Vr=[((z+1)²-1)/((z+1)²+1)]*c

possiamo ricavare la velocita' di recessione della galassia Z8-GND 5296 che risulta essere di 3*10⁸ m/s. Utilizzando la legge di Hubble possiamo stabilire la distanza rispetto alla terra pari a

d=Vr/H=0.13*10²⁵ metri

d=0.13*10²⁷*10^-16=0.13*10¹¹=13*10⁹ anni luce

essendo

1 m=10^-16 anni luce

Quindi la galassia Z8-GND 5296 si stava allontanando da noi ad una velocita' di 300 milioni di m/s, e si trovava ad una distanza di 13 miliardi di anni luce quando ha emesso la luce che Hubble ha raccolto. La luce raccolta e' stata emessa appena 700 milioni di anni dopo il Big Bang. E in questo momento dove si trova questa Galassia? Poiche' l'universo sta accelerando di sicuro ad una distanza maggiore di quando la luce raccolta da Hubble parti per il suo lungo viaggio verso la terra e cioe' maggiore di 13 miliardi di anni luce. Utilizzando il grafico di cui abbiamo gia' parlato che lega la distanza comovente con il parametro z si calcola infatti un valore di circa 30 miliardi di anni luce. In definitiva, come conseguenza dell'espansione dell'universo che puo' avvenire ad una velocita' maggiore di quella della luce ci troviamo nella situazione in cui per molte galassie non potremo avere piu' nessun tipo di contatto trovandosi queste al di la' dell'universo osservabile. Per altre riceveremo ancora un segnale e quindi saranno visibili fino a quando non oltrepasseranno l'universo osservabile e altre ancora che oggi non sono visibili perche' troppo lontane, che appariranno ai nostri occhi appena la luce ci raggiungera'. Questo l’universo osservabile. E quello che e’ nascosto a noi quanto e’ grande? Dipende dalla sua forma. Secondo la relativita’ generale la foma a sua volta dipende da quanta materia/energia c’e’ nell’Universo visto che essa curva il tessuto spazio-temporale. Gli scienziati hanno calcolato una densita’ critica d_c direttamente proporzionale al quadrato della costante di Hubble H, cioe’

d_c=k_*H²

dove k e’ una costante. Il rapporto tra la densita’ misurata e quella critica in genere viene indicata con la lettera greca omega. La densita’ critica e’ quella che rende l’energia cinetica dell’espansione uguale all’energia potenziale gravitazionale del volume che si sta espandendo. Consideriamo una sfera piena di galassie centrata nella nostra posizione. Sia r il raggio di questa sfera e d la densita’ di materia al suo interno. Una galassia di massa m e a distanza r subira’ un’attrazione della materia contenuta in tale sfera di massa totale M, e quindi l’energia potenziale dell’espansione sara’

(G_*m_*M)/r=(G_*m_*d_*4/3_*p_*r³)/r

dove G e’ la costante gravitazionale e p la costante pi-greco (3.14…).

Uguagliando questo valore a quello dell’energia cinetica:

1/2_*mv²=1/2_*m_*H² _*r²

dove H e’ la costante di Hubble, otteniamo che la densita’ critica e’ data da:

d_c = (3/8_*H²)/(p_*G)=10^-29 g/cm³

Se la densita’ dell’Universo fosse minore di quella critica cioe’ se omega fosse negativa, allora non ci sarebbe abbastanza materia per fermare l’espansione del cosmo, che continuerebbe per sempre. La forma risultante sarebbe curvata come la superficie di una sella. Questo e’ conosciuto come un Universo aperto.

Se la densita’ fosse maggiore di quella critica (omega positiva) allora ci sarebbe abbastanza materia per fermare l’espansione dell’Universo. In questo caso l’Universo risulterebbe chiuso e finito e avrebbe una forma sferica. Una volta che l’universo arresta la sua espansione iniziera’ a contrarsi e le galassie ad avvicinarsi sempre di piu’. Probabilmente in questo caso l’Universo subira’ un processo inverso del Big Bang, chiamato Big Crunch. Questo e’ conosciuto come un Universo chiuso. Se l’Universo invece contenesse una quantita’ di materia tale da far si che la densita’ sia uguale a quella critica, allora il tasso di espansione diminuira’ lentamente in un tempo infinito. In questo caso l’Universo e’ considerato piatto e di dimensione infinita.

Detto cio’ e’ ovvio che ci chiediamo quale e’ il valore della densita’ o anche del parametro omega dell’Universo.

Per stabilirlo bisogna conoscere quanta materia e radiazioni ci sono nel cosmo. La materia ordinaria e’ presente in diverse forme: pianeti, stelle, polveri, gas interstellare e intergalattico. Se valutiamo la densita’ di questa materia al massimo otteniamo circa il 5% della densita’ critica. Anche la radiazione e’ presente in grande quantita’ come energia elettromagnetica o come particelle relativistiche. Ma essa rende conto di meno del 1% della densita’ critica. Quindi se nell’universo ci fossero solo queste due forme di massa-energia, la densita’ sarebbe inferiore a quella critica, e l’universo continuerebbe ad espandersi senza fine. Sappiamo, pero’, che nell’Universo esiste un’altra forma di massa-energia, la cosiddetta “materia oscura”. Essa e’ stata introdotta per spiegare i movimenti delle stelle nelle galassie e delle galassie negli ammassi di galassie. Le stelle periferiche di una galassia per esempio, si muovono cosi’ velocemente che volerebbero via se non ci fosse una quantita’ significativa di materia superiore a quella visibile all’interno della galassia, capace di attirarle verso il centro compensando la forza centrifuga. Cosa sia la materia oscura ancora non si sa e non si sa nemmeno quanta ce ne sia. Le misure piu’ recenti tendono a convergere ad una stima di circa il 25% della densita’ critica.

Esiste un quarto contributo possibile alla composizione dell’Universo, che e’ stato ipotizzato per spiegare l’osservazione dell’accelerazione dell’espansione dell’Universo. Questo significa che nell’universo deve essere presente una strana forma di energia a pressione negativa che e’ stata chiamata energia oscura. Questa produce una repulsione e quindi aiuta l’espansione dell’Universo, facendola accelerare non appena diventa la forma di energia dominante. In base ai calcoli piu’ recenti tale energia dovrebbe costituire circa il 70% della densita’ critica e quindi essere la componente piu’ importante del nostro Universo. Una forma di energia con le stesse caratteristiche di quella oscura potrebbe essere l’energia del vuoto, misurata sperimentalmente e dovuta alla creazione e annichilazione continua di particelle-antiparticelle. La fisica fondamentale pero’ prevede un valore per questa energia decisamente piu’ alto di quello misurato e quindi al momento non esiste una teoria soddisfacente del fenomeno. A causa delle grosse incertezze sulla materia oscura e sull’energia oscura e’ praticamente impossibile stabilire se la densita’ totale dell’Universo sia superiore, inferiore o uguale a quella critica. Bisogna trovare quindi un modo indipendente per stimare la densita’ dell’Universo. Gli scienziati hanno pensato di usare la geometria e curvatura dello spazio tempo, misurando gli effetti che questa produce sui raggi di luce provenienti da distanze enormi. Come gia’ detto prima, la massa-energia presente nel nostro Universo secondo la relativita’ generale tendera’ a curvare lo spazio-tempo sia a grandi che a piccole scale. Dalle equazioni della relativita’ generale ci aspettiamo una curvatura positiva se il parametro omega e’ maggiore di 1, nulla se omega e’ uguale a 1 e negativa se omega e’ minore di 1. La curvatura su larga scala agira’ sui raggi di luce di oggetti molto lontani. Se la curvatura dello spazio tempo fosse positiva i raggi di luce convergerebbero e quindi le sorgenti apparirebbero piu’ grandi come succede quando viene utilizzata una lente di ingrandimento. In caso di curvatura negativa accadrebbe esattamente il contrario con le sorgenti che apparirebbero piu’ piccole, come dietro ad una lente divergente. Se esistesse un metodo per stabilire se la luce proveniente da sorgenti lontanissime viaggia in linea retta oppure no, potremmo determinare la geometria globale dell’Universo e quindi omega. Questo approccio e' stato tentato a lungo in passato, utilizzando le galassie lontane come sorgenti dei raggi di luce. Ma le galassie piu' lontane sono anche viste in un’ epoca piu' antica della loro evoluzione, e risultano essere irregolari, per cui e' difficile capire se eventuali deformazioni delle loro immagini siano dovute ad una eventuale curvatura dei raggi di luce durante il loro cammino, o siano piuttosto il risultato della irregolarita' delle sorgenti. Come si fa allora a misurare la curvatura dell’Universo? Ricorrendo a quella che gli scienziati chiamano radiazione cosmica di fondo. Vediamo di cosa si tratta. L’universo subito dopo il Big Bang subi’ tutta una serie di transizioni fino ad arrivare in uno stato di plasma (elettroni, protoni, nuclei di He e fotoni) dopo 380000 anni. A causa della diminuzione di temperatura in questo momento l’Universo cessa di essere un plasma e si formano i primi atomi cosi come li conosciamo noi. I fotoni smettono di interagire con le altre particelle (con la temperatura diminuisce la loro energia) e da questo momento in poi non potranno fare altro che iniziare a vagare per il cosmo senza piu’ interagire con la materia. Dunque ancora oggi dopo 13.7 miliardi di anni di vita questa radiazione pervade l’intero Universo ( si tratta di microonde come quelle dei forni usati in cucina) e che noi chiamiamo radiazione cosmica di fondo o piu’ semplicemente radiazione fossile. Oggi per ogni metro cubo di spazio ci sono circa 200 milioni di fotoni fossili e questi non avendo interagito con nulla trasportano informazioni relative all’Universo di 380000 anni dopo il Big Bang. La temperatura o energia di questa radiazione oggi e’ di solo 2.725 gradi Kelvin (cioe’ circa 270 gradi sotto lo zero) mentre all’inizio era di circa 3000 K. Il raffreddamento della radiazione fossile e’ avvenuto in conseguenza del fatto che tutte la dimensioni dell’Universo sono aumentate di un fattore dato dal rapporto 3000/2.725=1100. Ricordiamo infatti che dalla prima legge della termodinamica in caso di processo adiabatico se il volume di un gas aumenta allora la temperatura diminuisce. Una misura accurata della radiazione fossile e’ stata eseguita prima dal satellite WMAP e dopo dal satellite Planck, che oltre al valore medio della temperatura di 2.725 K hanno anche misurato delle piccolissime fluttuazioni di temperatura dipendenti dalla direzione da cui proviene la radiazione. Si tratta di fluttuazioni veramente piccolissime (decimillesimo di grado) ma nonostante cio’ sono molto importanti per dare diverse risposte sull’Universo appena nato. In effetti WMAP/Plank hanno scattato una fotografia dello stato termico dell’Universo come si presentava circa 13.7 miliardi di anni fa

Dall’analisi della mappa della radiazione fossile si e’ scoperto che approssimativamente tutte le macchie che indicano una fluttuazione di temperatura hanno le stesse dimensioni. Ma come mai ci sono queste fluttuazioni? Esse hanno avuto origine in una frazione di secondo dopo il Big Bang e consistevano di addensamenti o di rarefazioni locali di materia e di fotoni. La materia contenuta in queste fluttuazioni tendeva ad attrarre materia verso il centro grazie alla forza gravitazionale mentre i fotoni tendevano a farla espandere a causa della pressione di radiazione. Si trattava quindi di sistemi non in equilibrio che si espandevano e si contraevano rispetto alla loro posizione di equilibrio. In pratica l’Universo vibrava come vibra l’aria a causa di un suono. Al momento del disaccoppiamento tra materia e radiazione ogni fluttuazione e’ stata sorpresa in qualche istante della sua oscillazione. Poiche’ la crescita e contrazione avvengono ad una velocita’ pari a c/3^1/2 dove c e’ la velocita’ della luce, al momento del disaccoppiamento della materia le dimensioni di tali fluttuazioni erano:

3*10⁸/3^1/2 m/s * 380000 *3*10⁷ s=2*10²¹ m

A partire da quel momento l’estensione delle fluttuazioni e’ cresciuta insieme all’universo espandendosi di circa 1100 volte (cosi come qualsiasi altra dimensione del cosmo). Quindi oggi l’estensione di queste fluttuazioni dovrebbe essere:

h=1100*2*10²¹ =2.2*10²⁴ m

Proviamo a fare adesso un piccolo calcolo. Da quando l’Universo e’ iniziato la radiazione ha percorso quasi

L=3*10⁸*13.7*10⁹*365*24*3600=1.2*10²⁶ m

Se l’universo avesse una curvatura nulla, allora i raggi di luce provenienti dalle fluttuazioni primordiali formerebbero un triangolo e noi dovremmo osservare queste fluttuazioni sotto un angolo dato da:

h/L=2.2*10²⁴/1.2*10²⁶ radianti=1 grado

o sotto un angolo minore/maggiore se lo spazio avesse una curvatura negativa/positiva.

Le misure piu’ recenti indicano che l’Universo sia piatto, suggerendo quindi che sia anche infinito, cosa che non potremo mai verificare con i nostri telescopi essendo l’Universo visibile limitato.

Ma come mai tra tutti i possibili universi variamente curvi il nostro e’ proprio piatto? Come e’ potuto succedere che la densita’ media della materia e dell’energia abbia assunto tra gli infiniti valori possibili proprio il valore che rende piatto lo spazio-tempo? Al momento nessuno lo sa.

Una nuova fisica al lavoro nell’Universo?

Nel 1929 Hubble annunciò che la velocita’ radiale delle galassie era proporzionale alla loro distanza. In altre parole piu’ una galassia e’ distante da noi, piu’ la sua velocita’ di allontanamento e’ elevata. Il grafico seguente mostra i dati raccolti da Hubble con la velocita’ delle galassie riportata in ordinata e le loro distanze sulle ascisse:

La pendenza della retta che interpola queste misure è ora nota come costante di Hubble H. Dato che sia i kilometri che i Megaparsec sono unità di distanza, l'unità di misura di H è [1/tempo], essendo la velocita’ il rapporto tra spazio e tempo. Ma cosa rappresenta H? Il suo inverso e’ proprio l’eta’ dell’universo secondo la relazione di Hubble:

V=HD      da cui     D=V/H=Vt   con    t=1/H   appunto l’eta’ dell’universo.

Hubble trovo’ per il rapporto 1/H il valore di circa 2 miliardi di anni. Dal momento che tale valore dovrebbe approssimare l'età dell'Universo, e noi sappiamo (era noto anche nel 1929) che l'età della Terra supera i 2 miliardi di anni, il valore di H trovato da Hubble portò ad un generale scetticismo nei confronti dei modelli cosmologici, e fornì una motivazione a favore del modello stazionario, cioe’ quello di un universo non in espansione.

Tuttavia, pubblicazioni successive misero in luce alcuni errori compiuti da Hubble nelle sue misure. La correzione di questi errori portò ad un ridimensionamento verso il basso del valore della costante di Hubble. Attualmente il valore della costante e’ di 65±8 km/s/Mpc.
Con questo valore di H, l'età approssimativa dell'Universo è di 15 miliardi di anni. Qui di seguito i risultati recenti sulla relazione di Hubble la cui pendenza e’ pari a 65 Km/sec/Mpc.

Ma come faceva Hubble a misurare la velocita’ di una galassia lontana? Utilizzando quello che va sotto il nome di spostamento verso il rosso (redshift). La luce o una qualsisi altra radiazione elettromagnetica emessa da un oggetto in movimento ha una lunghezza d'onda maggiore di quella che aveva all'emissione. Ciò equivale a dire che nel caso della luce il colore si sposta nella direzione del rosso che e’ l'estremo inferiore dello spettro del visibile. Al contrario se un’oggetto si sta avvicinando la luce emessa si sposta verso il blu.

Se indichiamo con L_e la lunghezza d’onda emessa e con L_o quella osservata e’ possibile scrivere:

1+ z=[(1+v/c)/(1-v/c)]^1/2

dove c indica la velocita’ della luce, v la velocita’ dell’oggetto e il parametro z e’ dato da:

z=(L_o-L_e)/L_e

Quindi dalla misura di z cioe’ dello shift della luce si puo’ risalire alla velocita’ dell’oggetto che ha emesso la luce.

Per misurare la distanza delle galassie invece, Hubble aveva a disposizione tre metodologie ognuna valida per un certo intervallo di distanze. Il metodo piu’ antico e’ quello della parallasse che va bene per stelle non oltre i 500 anni luce. Si tratta di una tecnica geometrica che sfrutta lo spostamento delle stelle in primo piano rispetto a quelle fisse dovuto alla rotazione della terra intorno al sole. Il secondo metodo e’ quello delle Cefeidi, un tipo di stelle la cui luminosita’ varia periodicamente e che permettono di calcolare la loro distanza sfruttando la relazione tra quest’ultima e il periodo della loro luminosita’. L’intervallo di applicabilita’ va fino a circa 10 milioni di anni luce. L’ultimo metodo e’ quello delle supernove. Valutando l’andamento della luminosita’ di queste stelle subito dopo la loro esplosione e’ possibile calcolarne la luminosita’ assoluta e quindi la loro distanza. Questa tecnica permette di arrivare a distanze di alcune centinaia di milioni di anni luce.

Ma ritorniamo adesso alla costante di Hubble. E’ di qualche mese fa la notizia dell’utilizzo del telescopio spaziale Hubble per stabilire la misura piu’ precisa mai ottenuta della costante di Hubble. I risultati sono molto intriganti e sembrano evidenziare che ci sia qualche cosa di inaspettato al lavoro nell’universo. Questo perche’ i risultati confermano una fastidiosa discrepanza che mostra l’universo espandersi piu’ velocemente di quanto previsto dai dati relativi ai primi istanti del big bang. Il team di ricercatori capeggiato dal premio Nobel, Riess incluso anche l’italiano Stefano Casertano e Johns Hopkins, ha utilizzato Hubble per 6 anni aumentando il numero di stelle analizzate e con distanze fino a 10 volte maggiori di quelle ottenute precedentemente. Il valore della velocita’ di espansione ottenuto mostra una discrepanza di circa il 9% rispetto a quello previsto considerando i primi 378.000 anni dopo il Big Bang. Prima delle misure del telescopio Hubble, quelle effettuate dalla Agenzia spaziale Europea grazie al satellite Planck, avevano previsto per la costante di Hubble un valore intorno a 67 Km/sec per Megaparsec e non piu’ alto di 69 Km/sec/Mpc. Ma le misure recenti ottenute dal team di Riess riportano un valore della costante di Hubble di ben 73 Km/sec per Megaparsec, indicando che le galassie si stanno muovendo ad una velocita’ di allontanamento maggiore di quella prevista. I risultati della misura della costante di Hubble sono cosi precisi che gli astrofisici non possono non tener conto di questa incongruenza. Il team ritiene che alcune delle possibili spiegazioni per questa differenza siano legate all’universo oscuro che e’ il 95% della materia/energia contenuta nel nostro universo. La materia normale come stelle, pianeti e gas si crede costituisca solo il 5% del nostro universo. Il rimanente per il 25% e’ materia oscura e il 70% energia oscura, entrambi invisibili e mai rilevati in modo diretto. Vediamo la prima possibilita’. L’energia oscura, gia’ conosciuta in passato come fattore di accelerazione del nostro universo, sta spingendo lontano da noi le galassie con molta piu’ forza di quanto previsto. Questo potrebbe significare che l’accelerazione stessa potrebbe non essere costante ma cambiare nel tempo. Se questo fosse vero bisognerebbe allora rivedere il cosiddetto modello ACDM (Lambda cold dark matter) che spiega l’accelerazione del cosmo con la comparsa e scomparsa di particelle virtuali nello spazio vuoto che stirano lo spazio-tempo. Questo continuo ribollire del vuoto infatti non potrebbe spiegare un accelerazione che cambia col tempo.

Un’altra idea e’ quella che l’universo contenga delle nuove particelle subatomiche che viaggiano ad una velocita’ prossima a quella della luce. Si tratta di particelle velocissime, chiamate collettivamente “radiazione oscura”. Probabilmente si tratta di qualche cosa simile alle note particelle chiamate neutrini, creati nelle reazioni nucleari e nei decadimenti radioattivi. Diversamente da un neutrino normale pero’ che interagisce tramite la forza debole, queste nuove particelle dovrebbero essere influenzate solo dalla forza di gravita’ ed e’ per questo che hanno ricevuto il soprannome di “neutrini sterili”. Per analogia con i fotoni che sono i mediatori della forza elettromagnetica tra particelle, i neutrini sterili dovrebbero essere i mediatori delle interazioni tra particelle di materia oscura. E come per le particelle di materia oscura, anche la radiazione oscura non interagisce con la materia nominale. L’ultima possibile spiegazione e’ che la materia oscura interagisca piu’ fortemente con la materia nominale e/o la radiazione di quanto assunto fino ad ora. Al momento il team di Riess non ha una risposta al problema anche se sta continuando a raccogliere misure di stelle lontane per cercare di abbassare ulteriormente l’incertezza e migliorare la precisione sul valore della costante di Hubble.

Dove e’ possibile arrivare partendo da questo risultato?

Guardando i risultati ottenuti fino ad oggi e’ possibile come riportato da Riess, che l’energia oscura giochi un ruolo importante anche se e’ piu’ probabile che sia una qualche nuova particella o qualche cosa che ha a che fare con come interagisce la materia oscura. Normalmente quest’ultima viene considerata come costituita da WIMP, cioe’ da particelle pesanti che interagiscono debolmente con la materia nominale. Bene e’ possibile che l’interazione in fin dei conti non sia cosi debole come pensato. Questo potrebbe cambiare le cose e dare origine ad un qualche cosa simile all’universo che vediamo noi.

E se lo dice il premio Nobel Riess forse c’e’ da credere. Aspettiamo con impazienza le prossime scoperte. Fate le vostre scommesse. La fisica sta diventando misteriosa e magica.

Come torturare i dati per farli parlare

Il post di oggi e’ anomalo. Non si tratta del solito articolo. Ma di due presentazioni fatte alcuni anni fa per introdurre le tecniche di data mining/machine learning e  un ottimo software free (Orange) che ognuno puo’ scaricare ed utilizzare per fare un po’ di pratica. In queste slides vengono descritti i concetti base del machine learning, delle tecniche analitiche e del data mining quali decision tree, clustering, analisi di Bayes, association rules, self organizing maps, supported vector machines, random forest etc . L’idea alla base di queste due presentazioni è stata quella di introdurre i partecipanti (adesso i lettori del blog) nel mondo degli algoritmi sviluppati dalla cosiddetta computer science di cui tanto si sente parlare in ambiti quale l’internet delle cose, automobili senza guidatori, robots, droni  solo per citarni alcuni.

Il machine learning e’ fondamentale nello studio dei sistemi complessi in cui a causa dell’elevato numero di componenti e delle loro interazioni fortemente non lineari non si possono modellizzare facilmente. L’unica possibilita’ e’ quella di mettere al lavoro gli analytics oggi disponibili per cercare nella vasta mole dei dati le relazioni fondamentali, i patterns piu’ importanti, le informazioni nascoste come pepite all’interno delle miniere. Gli algoritmi di machine learning permettono di tirare fuori dai dati le informazioni utili riducendo in modo opportuno il volume dei dati. Pensate ad una piramide. Man mano che si sale verso l’alto, cioe’ man mano che il volume diminuisce emerge l’informazione.  MI fermo qui e vi lascio alle circa 200 slides. Buona lettura.  

Data mining e machine learning

Introduzione ad Orange

Gallerie spazio-temporali per unire relativita’ e quantizzazione

Nel 1935, alcuni fisici pubblicarono due articoli in cui venivano introdotti due concetti chiave dell’attuale cosmologia: l’entaglement e i wormholes.

Vediamo un attimo di cosa si tratta partendo dall’entaglement. Secondo la meccanica quantistica, le particelle entagled rimangono connesse tra loro anche se si trovano a distanze quasi infinite. Qualsiasi azione eseguita su una delle due particelle influenza il comportamento dell’altra. Questo significa per esempio che se in seguito ad una misura dello spin di una delle due particelle lo si trova up, quello dell’altra anche se misurato un’istante dopo sara’ down. Lo spin in meccanica quantistica e’ una grandezza fisica associata alle particelle e che ne definisce il loro stato quantico. Questa grandezza e’ una forma di momento angolare, avendo in comune la stessa dimensione. Per analogia richiama alla mente la rotazione di una particella intorno al proprio asse.

L’entaglement ha luogo quando le particelle interagiscono tra loro fisicamente. Per esempio un laser colpendo un particolare tipo di cristallo puo’ generare coppie di fotoni entagled che pur allontanandosi tra loro sempre di piu’ rimangono in connessione. Questa teoria che irrito’ non poco Einstein e’ anche riferita come “la spaventosa azione a distanza”. Come e’ possibile che due particelle anche a distanze enormi possano influenzarsi a vicenda subito se qualsiasi segnale nell’universo non puo’ viaggiare a velocita’ maggiore di quella della luce?

Passiamo adesso ai wormhole. Grazie alla teoria di Einstein oggi sappiamo che la trama del nostro universo e’ lo spazio-tempo. Esso puo’ essere deformato e distorto. Per fare questo lo spazio-tempo ha bisogno di grandi quantita’ di massa o di energia, ma teoricamente queste distorsioni sono possibili. Nel caso di un wormhole, si tratta di una scorciatoia ottenuta grazie alla deformazione del tessuto spazio-temporale. Immaginiamo di disegnare due punti su di un foglio di carta e di misurarne la distanza. Adesso pieghiamo il foglio in due sovrapponendo i due punti e attraversandoli con una penna. La distanza tra essi e’ decisamente inferiore a quella di prima. E’ esattamente quello che succede con un wormhole. Il problema di queste strutture e’ che essi sono instabili. Quando una particella vi entra dentro crea delle fluttuazioni che fanno collassare la struttura.

Nel 2013 Leonard Susskind un fisico di Stanford e Juan Maldacena dell’Advanced Study of Princeton hanno ipotizzato che questi due fenomeni siano la stessa cosa e questo potrebbe creare un ponte tra la teoria della relativita’ generale e la meccanica quantistica. Uno dei problemi più difficili che la fisica oggi si trova ad affrontare riguarda proprio queste due teorie  che funzionano perfettamente nel loro dominio di validita’ e che vanno invece in conflitto quando si cerca di combinarle. Susskind e Maldacena hanno riassunto il tutto in un’equazione: ER=EPR.

Non si tratta di un’equazione numerica, ma piuttosto di un’equazione con le iniziali dei nomi di alcuni importanti fisici teorici.

Nella parte a sinistra, ER stanno ad indicare Einstein e Nathan Rosen che in un articolo del 1935 descrissero la struttura dei wormhole, noti tecnicamente come ponti di Einstein-Rosen. A destra, invece, EPR stanno per Einstein, Rosen e Boris Podolsky, quest’ultimo co-autore di un altro articolo di quello stesso anno in cui veniva descritto l’entanglement quantistico. L’equazione semplicemente getta un ponte tra i wormhole e l’entaglement. E questa connessione potrebbe spiegare la continuita’ dello spazio tempo che diventerebbe cosi la manifestazione geometrica dell’entaglement.

Susskind va oltre e pensa che l’entaglement quantistico sia una forma di informazione, una stringa di 1 e di 0, e che quindi lo spazio tempo altro non sia che una manifestazione dell’informazione quantistica. Il principio ER=EPR, getta le basi per lo sviluppo della gravita’ quantistica anche se al momento non e’ chiaro come. E’ possibile che quando in laboratorio creiamo per esempio dei fotoni entangled questi siano connessi tramite un microscopico wormhole? Al momento nessuno lo sa anche se e’ affascinante pensare di si. In un nuovo articolo Susskind propone uno scenario dove ipotizza che delle particelle inizialmente entagled (correlate) si muovano in direzioni opposte dell’universo. Una volta lontane tra loro queste particelle collassano in buchi neri soggette alla loro stessa forza di gravita’. Secondo Susskind questi due buchi neri sono a loro volta connessi (entangled) tramite un gigantesco wormhole che attraversa l’universo da una parte all’altra. Dunque se l’equazione ER=EPR e’ giusta vuol dire che i due buchi neri saranno collegati da un gigantesco tunnel spazio temporale e l’entaglement altro non e’ che la descrizione geometrica di tali oggetti.

Teoria a dir poco sbalorditiva. Ma c’e’ la possibilita’ di provarla? Difficile dirlo. Di sicuro ci sono sempre piu’ ricercatori che iniziano a studiare questa ipotesi ed e’ possibile che in un prossimo futuro si riesca a gettare luce su uno dei misteri della Natura che assilla le menti di molti scienziati da quasi un secolo.

Secondo Susskind, “sembra ovvio che se ER = EPR è vera, allora siamo di fronte a qualcosa di grosso che potrebbe influenzare le fondamenta e le interpretazioni della meccanica quantisica. Se ho ragione, la meccanica quantistica e la gravità sono ancora di più correlate di quanto (almeno io) abbiamo mai pensato”.

https://arxiv.org/pdf/1707.04354

https://arxiv.org/pdf/1306.0533.pdf

https://arxiv.org/pdf/1604.02589