Terremoti ed Internet. Simili ma non troppo

Visto i recenti avvenimenti dell’Emilia Romagna credo di fare cosa gradita ai frequentatori di questo blog pubblicando il capitolo 33 del mio libro L’Universo dei numeri, i numeri dell’universo. Buona lettura.

I terremoti sono fenomeni naturali che si verificano continuamente in zone ben precise della crosta terrestre, in relazione a complicati processi di evoluzione del nostro pianeta. Le aree, più frequentemente colpite dai terremoti, sono quelle che si trovano ai limiti delle placche o zolle, in cui è divisa la parte più esterna della terra (litosfera) secondo la teoria della tettonica a zolle. I terremoti avverrebbero proprio ai margini di tali blocchi, in quanto essi si avvicinano, si allontanano, oppure scorrono l’uno accanto all’altro provocando notevoli deformazioni della litosfera fino ad arrivare a delle fratture chiamate faglie, lungo le quali si verificano più facilmente le successive rotture della crosta terrestre (vedi figura 33.1).

Lungo queste fratture si generano intensi rilasci di energia sottoforma di onde meccaniche, definite appunto "onde sismiche". In generale, l’energia durante un terremoto, viene rilasciata tramite una forte scossa principale, per lo più preceduta da piccole scosse premonitrici, dette foreshocks, e seguita da una serie di numerosissime scosse dette aftershocks. Il volume di roccia da cui si origina la frattura e da cui quindi parte la propagazione delle onde sismiche, prende il nome di fuoco. Per semplicità, l’ubicazione della zona sorgente si assimila ad un punto denominato ipocentro; il suo corrispondente sulla superficie terrestre si chiama invece epicentro. I sismologi classificano i terremoti, in base alla profondità del loro ipocentro: superficiali (0-70 km), intermedi (70-300 km) e profondi (300-720 km). I terremoti superficiali sono quelli potenzialmente più distruttivi e pericolosi per gli insediamenti umani. Il meccanismo alla base dei terremoti è stato compreso in seguito alle ricerche del geologo F. Reid ed è da ricercare, come già detto, nelle forze tettoniche che continuano a deformare lentamente le rocce della crosta terrestre lungo le linee di separazione delle placche.

Figura 33.1 Le placche della litosfera (sinistra) e la distribuzione dei terremoti (destra).

Le rocce, che si deformano, immagazzinano energia elastica, proprio come fa un bastone, quando viene incurvato. Quando le forze di legame delle rocce vengono superate, si ha un brusco spostamento delle rocce nel punto più debole della faglia. Il movimento in quel punto (ipocentro del terremoto) provoca istantaneamente una deformazione più in là lungo la faglia, e qui si potrà verificare un ulteriore slittamento; il processo si ripete fino a, quando non si sarà liberata la maggior parte dell’energia elastica immagazzinata. Questo spostamento permette alla roccia deformata di ritornare di colpo alla sua posizione originale, producendo onde sismiche (vedi figura 33.2). Un parametro importante per caratterizzare un terremoto è la sua intensità; questa viene misurata per mezzo di due scale, che prendono il nome dagli scienziati che le hanno sviluppate: Mercalli e Richter. La Scala Mercalli è divisa in 12 gradi d’intensità crescente ed è basata sull’osservazione degli effetti del terremoto partendo da un valore 1 (impercettibile) fino ad un valore 12 (totalmente catastrofico). È opportuno sottolineare che con tale scala si misura l’intensità, cioè esclusivamente gli effetti che un terremoto produce sulle costruzioni, sul terreno e sugli insediamenti umani. La Scala Richter, invece, misura quantitativamente l’energia trasportata dalle onde sismiche secondo una scala che va da valori bassi, anche negativi, fino a valori compresi tra 8 e 9, misurati da appositi strumenti; con questa scala, quindi, si effettua una misura più oggettiva, cioè si calcola la magnitudo. La magnitudo (indicata con M) è una misura dell’energia rilasciata durante un terremoto nella porzione di crosta dove questo si genera.

 

Figura 33.2 Modello della tettonica a zolle.

I terremoti sono caratterizzati da una fenomenologia molto ricca, che da sempre ha attratto l’attenzione di fisici e matematici che li hanno considerati dei sistemi complessi non facili da analizzare. Questo perchè sia l’ampiezza che il luogo in cui un terremoto si presenta sono intrinsecamente probabilistici.

I sismologi hanno identificato due leggi empiriche che regolano i terremoti. Una è la legge di Gutenberg-Richter, che stabilisce che la frequenza dei terremoti obbedisce ad una legge di potenza rispetto all’energia rilasciata. Questa legge di potenza rende inutile ogni tentativo di distinguere statisticamente i terremoti in base alla loro magnitudo a causa dell’assenza di una scala tipica di energia. La presenza di una legge di potenza per l’energia rilasciata dai terremoti significa che in natura molto spesso i terremoti sono di bassa intensità e raramente solo sono catastrofici. Ma il meccanismo che regola le scosse di bassa intensità è lo stesso di quello che regola le scosse di alta intensità.

L’altra legge è quella di Omori, che stabilisce che il numero di scosse d’assestamento dopo la scossa principale segue una legge di decadimento del tipo:

dove p è una costante che varia da 0.5 a 2.5 con un valore tipico vicino ad 1. Questa legge stabilisce che il numero di scosse di assestamento diminuisce rapidamente subito dopo la scossa principale e poi molto lentamente nel tempo. I terremoti mostrano, anche, una struttura frattale sia da un punto di vista spaziale che temporale. Analizzando la distribuzione degli epicentri dei terremoti di particolari regioni della terra come quella mostrata in figura 33.3, i ricercatori hanno verificato che questi tendono a distribuirsi in clusters senza una particolare scala. Coprendo l’immagine della figura 33.3, con un reticolo di lunghezza fissata e colorando i quadratini di nero se in essi cade almeno un punto dell’epicentro di un terremoto, ci si accorge che la distribuzione spaziale originaria non cambia all’aumentare della dimensione dei quadrati del reticolo. A tutte le scale l’immagine che ne risulterà sarà sempre la stessa. Usando le tecniche descritte nel capitolo X, gli scienziati hanno calcolato una dimensione frattale tipica dei terremoti di circa 1.5. Lo stesso discorso vale anche considerando gli intervalli temporali che intercorrono tra i terremoti in un determinato arco temporale. Come si può vedere dalla figura 33.4, la distribuzione temporale dei terremoti con magnitudine maggiore di 6 non è del tutto casuale in quanto c’è un chiaro fenomeno di raggruppamento (clustering). Per capire se anche in questo caso abbiamo una mancanza di scala si può dividere l’asse temporale della figura 33.4, in intervalli temporali di diverse lunghezze come mostrato in figura 33.5. Si nota immediatamente che il comportamento generale della frequenza per una data scala appare simile a quello delle altre scale (invarianza di scala). Quello che è interessante è la ricorrenza dei picchi allo stesso istante su tutte le scale di tempo. Una chiara indicazione di una struttura frattale essendo gli eventi altamente localizzati nel tempo e presenti con una probabilità che è indipendente dalla scala temporale. Per essere più precisi si tratta di una struttura multi frattale, cioè una collezione di monofrattali sovrapposti che dà luogo a degli intervalli temporali più densamente popolati e ad altri meno (vedi figura 33.6). Tutto ciò ha una forte somiglianza con i sistemi complessi in stati critici lontani dall’equilibrio. Poiché l’approccio delle reti complesse si è dimostrato essere un potente mezzo per analizzare le strutture cinematiche e dinamiche dei sistemi complessi, alcuni ricercatori lo hanno applicato anche allo studio dei terremoti. In questo caso la rete viene costruita nel seguente modo. La regione geografica di interesse viene divisa in tante piccole celle di forma cubica. Una cella viene vista come un vertice (nodo) della rete se all’interno di essa si è manifestato un terremoto di qualsiasi magnitudo. Due terremoti successivi definiscono un arco tra due vertici. Se essi capitano nella stessa cella allora l’arco si richiude sullo stesso vertice (loop). Questa procedura rende possibile la mappatura degli eventi sismici tramite un grafo probabilistico dinamico, che chiameremo la rete dei terremoti.

 

Figura 33.3 Mappa dei terremoti avvenuti in Anatolia tra il 1900 e il 1992.

 

Figura 33.4 Momento sismico (una grandezza equivalente all’energia rilasciata durante un terremoto) nel tempo (in secondi). Il periodo temporale è 1984-2002. Sono stati considerati solo i terremoti con magnitudine maggiore di 6.

 

Figura 33.5 Evoluzione temporale degli eventi sismici avvenuti nella regione dell’Anatolia a differenti scale temporali.

 

Figura 33.6 Metodo per costruire un multi frattale. Si parte col considerare n eventi distribuiti su un intervallo temporale di lunghezza 4, lasciando vuoto il secondo sito. Alla seconda iterazione, la nuova distribuzione è la somma della configurazione per n=1 più una sua versione ingrandita due volte.

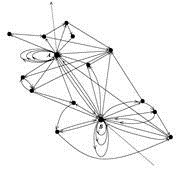
In questo modello, gli archi della rete rappresentano la correlazione tra gli eventi sismici (vedi figura 33.7). Dall’analisi di un tale modello emerge la presenza di alcuni nodi che corrispondono alle scosse principali con un numero molto elevato di connessioni (hubs). Ciò è in accordo con quanto scoperto dall’analisi dei dati reali che mostrano che le scosse di assestamento tendono sempre a ritornare nel luogo della scossa principale. Questo è il motivo per cui un nodo che rappresenta una scossa principale tende ad avere un numero elevato di connessioni, cioè tende a diventare un hub. Come mostrato in figura 33.8, la distribuzione delle connessioni segue una legge di potenza del tipo:

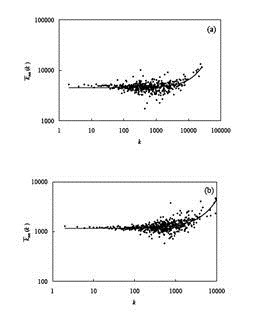
dove gamma è una costante positiva. Questo significa che la rete dei terremoti è una rete senza scala (scale-free), in accordo con la legge di Gutenberg-Richter, che stabilisce che la frequenza dei terremoti decade lentamente secondo una legge di potenza rispetto all’energia rilasciata. Dall’analisi della rete dei terremoti è emerso, anche, un rapporto dei coefficienti di clustering che può variare tra 50 e 100 a secondo della dimensione del reticolo utilizzato. Essendo il coefficiente di clustering notevolmente più grande di quello delle reti casuali e poiché la distanza media della rete dei terremoti è molto piccola, questo dimostra in modo inequivocabile che la rete dei terremoti è una rete di piccolo mondo. Per poter andare avanti con l’associazione tra terremoti e reti bisogna introdurre un’altra caratteristica importante delle reti complesse: l’organizzazione gerarchica. Per dimostrare che una rete è organizzata in modo gerarchico va analizzato il coefficiente di clustering in funzione del numero di connessioni di ogni nodo k. Se esso segue una legge di potenza del tipo:

allora la rete ha una struttura gerarchica. Questo è esattamente il caso della rete dei terremoti come si può vedere dalla figura 33.9. La presenza di una struttura gerarchica è molto importante da un punto di vista fisico. Per poterla spiegare, infatti, bisogna assumere che la regola “i ricchi diventano sempre più ricchi” non è vera per tutti i nodi della rete dei terremoti. Alcuni di questi associati a delle faglie attive possono disattivarsi attraverso il processo di rilascio dello stress da parte della faglia e quindi non possono più ricevere nuove connessioni.

 

Figura 33.7 Rete dei terremoti della California nel periodo 1984-2003.

 

Figura 33.8 Distribuzione delle connessioni per la rete dei terremoti della California nel periodo 1984-2003. In a è stato usato un reticolo con dimensioni 10x10x10 Km mentre in b un reticolo 5x5x5 Km.

La struttura gerarchica scompare se vengono rimosse le connessioni deboli (per esempio i terremoti con una magnitudo minore di 3).

 

Figura 33.9 Distribuzione del coefficiente di clustering per la rete dei terremoti della California nel periodo 1984-2003. In (a) è stato usato un reticolo con dimensioni 10x10x10 Km mentre in (b) un reticolo 5x5x5 Km.

La natura scale-free, il fenomeno di piccolo-mondo, la crescita inomogenea delle connessioni e la struttura gerarchica indicano che la rete dei terremoti è molto simile a quella di Internet, anche se differiscono in un punto. Si tratta della proprietà di correlazione delle connessioni. Essa indica qual è la probabilità che un nodo con molti gradi (pochi gradi) sia connesso ad uno con molti gradi o ad uno con pochi gradi. Se questo parametro tende ad aumentare al variare del numero di gradi k allora la rete è detta assortiva mentre se il parametro tende a diminuire la rete è detta disassortiva. Per la rete dei terremoti si trova una correlazione che tende ad aumentare come mostrato in figura 33.10, indicando che i terremoti costituiscono una rete assortiva. Perciò, i nodi con un numero elevato di connessioni tendono ad essere collegati uno all’altro, cioè i nodi che rappresentano terremoti più intensi, tendono ad essere connessi tra loro. Al contrario, Internet, è una rete disassortiva e quindi ha esattamente il comportamento opposto di quello della rete dei terremoti.

Altra caratteristica molto importante dei terremoti e la loro periodicità. Dopo quanto tempo mediamente un terremoto torna nel punto iniziale, cioè nel nodo iniziale della rete dei terremoti? Come mostrato in figura 33.11, la distribuzione dei periodi (che per una rete corrisponde al numero di connessioni Lp da attraversare) segue anch’essa una legge di potenza. Questo implica che ci sono terremoti con periodi molto lunghi, che, da un punto di vista statistico, rendono molto difficile stabilire dopo quanto tempo un terremoto si può ripresenterà in uno stesso luogo. Ciò rende quasi impossibile qualsiasi tipo di previsione.

Oltre all’approccio di rete complessa, i terremoti possono essere modellizzati efficacemente anche utilizzando la cosiddetta teoria SOC (Self-Organized criticality), secondo la quale i sistemi dinamici, lontani dall’equilibrio, possono evolvere spontaneamente verso uno stato critico, per un ampio intervallo di valori dei parametri caratteristici del sistema. Un esempio che illustra il meccanismo SOC è il cosiddetto modello del mucchietto di sabbia o “Sand-pile”. Si tratta di un piatto su cui si fanno cadere dall’alto, uno pera volta, dei granelli di sabbia. Questi granelli si disporranno in una struttura a “pila” di forma conica. Man mano che si aggiungono granelli di sabbia, la pendenza di questo cono aumenterà, fino a raggiungere un valore critico, oltre il quale qualsiasi aggiunta di granelli di sabbia determinerà delle valanghe che andranno a riempire gli spazi rimasti vuoti vicino alla pila di sabbia. Continuando ad aggiungere altra sabbia, il numero di granelli sovrabbonderà e cadrà al di là del piatto. Quando il numero dei granelli persi sarà uguale in media a quello dei grani aggiunti, il mucchietto raggiungerà il suo stato critico. Anche se questo modello è molto semplice, esso si adatta bene a descrivere molti sistemi fisici ed è in grado di generare distribuzioni con legge di potenza che come visto sono molto ricorrenti in natura.

 

Figura 33.10 Coefficiente di correlazione tra nodi al variare del numero di gradi k.

Gli aspetti fondamentali della teoria della criticità auto-organizzata possono essere cosi riassunti:

1. La distribuzione della dimensione delle valanghe segue una legge di potenza

2. Le leggi fisiche che regolano l’interazione tra i granelli di sabbia sono molto semplici. In altre parole per auto organizzarsi il sistema non ha bisogno di complicate leggi fisiche

3. Le valanghe non avvengono in modo periodico ma in modo imprevedibile

4. La superficie del mucchietto di sabbia mostra una struttura frattale

Come è possibile applicare questo modello ai terremoti? Basta ricordare che i terremoti sono associati allo scivolamento delle placche tettoniche lungo le faglie e che le forze tettoniche deformano lentamente le rocce della crosta terrestre lungo le faglie immagazzinando energia.

 

Figura 33.11 Coefficiente di correlazione tra nodi al variare del numero di gradi k.

Quando quest’ultima supera un valore critico, essa è rilasciata sotto forma di uno scivolamento di un blocco rispetto all’altro coinvolgendo un certo numero di blocchi vicini e dando luogo a “valanghe”. Il modello “sand-pile”, è stato proposto per la prima volta nel 1988 dallo scienziato Per Bak e può essere simulato usando una matrice con nxn celle, ognuna delle quali può interagire con le prime vicine (Nord, Sud, Est, Ovest). Ad ogni cella si attribuisce un valore numerico compreso in un certo intervallo come per esempio tra 1 e 14 e ad ogni numero viene associato un colore che va dal blu al rosso. Inizialmente le celle della matrice vengono forzate ad un valore tra 1 e 14 scelto in modo del tutto casuale (vedi figura 33.12).

 

Figura 33.12 Simulazione SOC. All’inizio il valore di ogni cella è del tutto casuale.

 

Si prende a caso una cella della matrice e si incrementa il suo valore numerico (che corrisponde allo stress o energia accumulata dalle rocce) di un’unità: questo processo corrisponde alla caduta di un granello di sabbia nel modello sand-pile ovvero ad un leggero aumento della tensione che si esercita tra blocchi (nel caso dei terremoti) o granelli contigui (nel caso del mucchietto di sabbia). Se il nuovo valore della cella è inferiore ad un valore critico Zc (che possiamo per esempio scegliere essere uguale a 14) allora si procede ad un’aggiunta di granelli altrimenti lo stress viene rilasciato ai primi 4 vicini. In quest’ultima ipotesi, bisogna valutare il valore numerico delle celle vicine e verificare se esso è inferiore o superiore al valore critico. Se è maggiore, allora, si procede analogamente a prima generando una valanga. Al termine di questa valanga, si procede all’aggiunta di ulteriori granelli di sabbia generando cosi ulteriori valanghe. C’è da tener presente comunque, una cosa molto importante. Inizialmente la matrice essendo in uno stato completamente casuale, non si trova in uno stato critico e quindi bisogna generare un certo numero di valanghe per portare il sistema in uno stato di criticità auto-organizzato, a partire dal quale una qualsiasi perturbazione genererà valanghe di differenti grandezze, la cui distribuzione seguirà una legge di potenza. Per determinare quando il sistema raggiunge lo stato critico si può fare nel seguente modo. Si segue la variazione nel tempo del valore medio di tutti gli elementi della matrice <z(t)>, cioè la somma dei valori della matrice diviso il numero totale delle celle e si verifica quando questo valore si porta ad un valore asintotico attorno al quale oscilla. Questo sarà lo stato critico (vedi figura 33.13) del sistema.

 

Figura 33.13 Simulazione SOC. Andamento del valore medio dei valori delle celle nel tempo.

 

Per l’esempio scelto, il valore critico è di circa 12.8. Quindi si registrerà una valanga solo se prima di aggiungere un granello di sabbia il valore medio di z è maggiore di 12.8. Facendo partire la simulazione, si osserveranno le diverse valanghe come mostrato in figura 33.14.

 

Figura 33.14 Simulazione SOC. Formazione delle prime valanghe col trascorrere del tempo.

 

I vari clusters di punti corrispondono alle celle che vengono interessate durante ogni valanga. Procedendo iterativamente con l’algo-ritmo si possono catalogare diverse valanghe in base alla loro dimensione. Una volta ottenuti questi risultati, si può riportare su scala bi-logaritmica la dimensione delle valanghe e quante volte ogni dimensione si è presentata (frequenza). La parte lineare di questo grafico segue una legge di potenza con un esponente uguale a circa -1 (vedi figura 33.15).

Ovviamente, la stessa simulazione può essere fatta anche partendo con una matrice iniziale non casuale ma con le celle in uno stato ben definito come mostrato in figura 33.16. In questo caso le celle centrali sono cariche di stress. Se si aggiungono a questa matrice altri grani, essa inizialmente conserva il ricordo della condizione iniziale, ma dopo un pò di tempo la tensione di stress accumulata al centro della matrice comincia a distribuirsi in modo eguale su tutti i siti. Dopo 500000 valanghe, la matrice si porta in uno stato di criticità auto organizzata, ed assume un aspetto simile a quello mostrato in figura 33.17.

 

Figura 33.15 Simulazione SOC. Legge di potenza.

 

Figura 33.16 Simulazione SOC. Celle centrali in uno stato critico.

 

Figura 33.17 Simulazione SOC. Stato finale della matrice della figura 33.16 dopo 500000 valanghe.

 

Questo risultato conferma l’ipotesi della teoria SOC, secondo cui il sistema lontano dall’equilibrio, indipendentemente dallo stato iniziale, si auto-organizza ed evolve verso uno stato critico. Anche per questa simulazione si può analizzare la distribuzione della dimensione delle valanghe, ottenendo per l’esponente della funzione potenza esattamente lo stesso valore precedente, cioè circa -1. Il grafico come quello mostrato in figura 33.15, riproduce qualitativamente la legge di Gutenberg-Richter dei terremoti. Nonostante la semplicità del modello SOC, se si variano opportunamente i pochi parametri della simulazione, è possibile ottenere diverse dinamiche con proprietà differenti. Che dire. Ancora una volta la matematica alla base di un semplice modello riesce a replicare il comportamento dei terremoti e di altri sistemi dinamici presenti in Natura. Delle semplice regole, e un numero elevato di parti connesse (interagenti) sono gli ingredienti giusti per dar vita a strutture complesse il cui comportamento non è prevedibile analizzando le sue parti.

E’ possibile che l’universo sia stato programmato per ospitare la vita?

Sara’ capitato a molti di voi di alzare lo sguardo al cielo in una notte buia e rendersi conto dell’immensita’ dell’universo, della sua bellezza e regolarita’. Tutto sembra funzionare alla  perfezione. Le leggi della fisica e i valori delle cosiddette costanti fisiche (come per es. la costante universale gravitazionale che regola l’attrazione tra due corpi massicci) sembrano essere quelle giuste affinche’ l’universo sia quello che e’. Se anche una delle proprieta’ fisiche fosse stata differente, le stelle, i pianeti e le galassie non si sarebbero mai formate. E la vita sarebbe stata impossibile.

Consideriamo per esempio il neutrone (la particella neutra presente nel nucleo degli atomi); esso e’ 1.00137841870 volte piu’ pesante del protone (l’altra particella presente nel nucleo con carica positiva) e questo fa si che il neutrone possa decadere in un protone, elettrone e neutrino (radiazione beta), un processo che ai tempi del Big Bang determino’ l’abbondanza di idrogeno ed elio e che fece si che il nostro universo fosse dominato dall’idrogeno. Se il rapporto delle masse del neutrone e del protone fosse stato leggermente diverso, noi vivremmo in un universo molto differente: uno per esempio in cui le stelle consumano velocemente il loro combustibile nucleare oppure uno in cui i protoni decadono in neutroni lasciando l’universo senza atomi. Universi che non hanno la possibilita’ di far evolvere la vita.

Voglio fare qui una breve divagazione nella fisica del chaos. Sicuramente molti di voi conosceranno l’effetto farfalla: un semplice battito d’ali in Brasile puo’ generare un tornado a New York. Questo perche’ il sistema dell’atmosfera terrestre e’ un sistema complesso con una dipendenza sensibile dalle condizioni iniziali. Qualche variazione inizialmente molto piccola puo’ essere amplificata nel tempo e diventare una variazione grandissima. Questo e’ tipico dei sistemi complessi che si trovano all’edge del chaos cioe’ in bilico tra un ordine perfetto e il disordine totale. Pensate alle transizioni di fase che portano un oggetto da solido a liquido e quindi in fase gassosa. La fase liquida puo’ essere considerata quella in bilico tra l’ordine perfetto dei reticoli cristallini dei solidi e il disordine totale delle molecole dei gas. Visto che il nostro universo ha una dipedenza sensibile dai valori delle costanti fisiche fondamentali sembra suggerire che esso possa essere considerato come un sistema complesso ai confini del chaos. E questo potrebbe spiegare perche’ in esso si e’ evoluta la vita. Sono in tanti gli scienziati che credono che solo nei sistemi all’edge del chaos si possa generare la vita in quanto non sono ne’ troppo ordinati da non potersi adattare alle condizioni esterne ne’ troppo disordinati da non riuscire ad imparare.

Esempi di valori di costanti fisiche regolate opportunamente per giustificare l’universo che oggi vediamo ce ne sono tanti. Se per esempio raddoppiassimo la carica di un elettrone, o cambiassimo di poco l’intensita’ della forza gravitazionale o della forza nucleare l’universo apparirebbe molto ma molto diverso.

La grande sfida per i fisici e’ di spiegare perche’ questi parametri hanno il valore che hanno e non un altro.         

E non solo. Un’ altra sfida e’ quella dell’energia oscura, l’energia che sta accelerando il nostro universo e di cui non conosciamo quasi nulla. Tutti i tentativi fatti dai fisici per determinare il valore aspettato di questa energia porta ad un valore 10^120 volte piu’ grande di quello aspettato.

Secondo il fisico Susskind dell’Universita’ di Stanford il grande mistero non e’ tanto spiegare perche’ esiste l’energia oscura quanto perche’ ce n’e’ cosi poca. Un valore leggermente piu’ alto avrebbe fatto espandere lo spazio-tempo cosi velocemente che le galassie non si sarebbero potute formare. 

Ci sono due possibili spiegazioni per un cosi’ perfetto “aggiustamento” delle costanti fisiche. Una e’ quella di far intervenire un Dio che ha programmato il tutto e l’altra che esista un grande numero di universi se non addirittura infiniti di cui il nostro e’ uno di essi

Questo insieme di universi e’ quello che i fisici chiamano il multiverso. In un multiverso le leggi fisiche e le costanti fondamentali sono diverse in ognuno dei suoi universi. Quindi il nostro non e’ particolare. Semplicemente ha avuto la fortuna di avere i valori giusti per far evolvere la vita. In altri universi meno fortunati questo purtroppo non e’ avvenuto. Questo e’ il cosiddetto principio antropico.  Non tutti i fisici pero’ condividono questa prospettiva. Lawrence Krauss dell’universita’ dell’Arizona, autore del libro “A Universe from nothing” vorrebbe capire perche’ l’universo e’ quello che e’ senza ricorrere alla casualita’ del multiverso.

Tuttavia l’idea del multiverso oggi sta prendendo sempre piu’ piede specialmente perche’ esso viene predetto da una teoria che e’ stata sviluppata per risolvere la questione della “piattezza” del nostro universo.

 

Tutte le misure effttuate fino ad ora hanno mostrato che il nostro spazio-tempo e’ piatto, cioe’ in esso vale la geometria Euclidea. Per esempio per un qualsiasi triangolo la somma degli angoli interni e’ sempre 180 gradi. Se lo spazio-tempo fosse stato curvato, invece questo non sarebbe stato vero. La “piattezza” del nostro spazio-tempo e’ stata confermata dalle misure accurate della radiazione cosmica di fondo, la luce che circa 380.000 anni dopo il Big Bang emerse dal nostro universo che fino a quel tempo era stato opaco assorbendo in continuazione i fotoni emessi all’atto del grande scoppio iniziale. 

Se l’universo e’ piatto questo implica che il parametro Omega, legato alla curvatura dello spazio-tempo e’ molto vicino al valore 1. E per avere oggi un universo con un valore Omega vicino a uno significa che un secondo dopo il Big Bang esso doveva avere un valore esattamente uguale a 1 con una precisione di decine di cifre decimali. Cosa ha fatto si che questo valore fosse esattamente uno e non un valore leggermente diverso?

La risposta e’ venuta nel 1979 dal fisico Alan Guth. Egli mostro’ che nei primi istanti dopo il Big Bang, l’universo subi’ un periodo di espansione esponenziale. Questa improvvisa espansione, che Guth chiamo’ inflazione rese il nostro universo osservabile piatto indipendentemente dal valore del parametro Omega prima dell’inflazione.

Alcuni fisici credono che l’inflazione continui ancora oggi in posti diversi e lontani dell’Universo, generando uno dopo l’altro nuovi universi ognuno con diverse proprieta’ fisiche. Questo e’ quello che viene chiamata l’eterna inflazione. Ogni universo e’ solo una piccola frazione di un universo piu’ grande che a sua volta e’ solo uno di un numero di altri infiniti universi. Ognuno di questi universi e’ il prodotto del suo proprio big bang. Questo multiverso puo’ essere rappresentato come un insieme di bolle. Ogni bolla rappresenta un universo infinito, e ci sono un infinita’ di bolle, cioe’ di universi.  

E’ possibile provare una tale ipotesi? Sembrerebbe di si. Se esistono infiniti universi allora e’ possibile che ci siano state nel passato delle collisioni tra essi lasciando un’impronta nella radiazione cosmica di fondo: dei cerchi concentrici in cui la temperatura dovrebbe essere leggermente diversa dalle zone circostanti.

L’analisi dei dati del satellite WMAP non ha evidenziato con certezza nessuna regione con questa forma anche se alcuni studiosi tra cui Stephen Feeney dell’University College London dicono di aver trovato qualche possibile prova di questi pattern circolari nella radiazione cosmica di fondo (vedi immagine sopra).

Qualche cosa di analogo sembra essere stato individuato anche da Roger Penrose e V. Gurzadyan come emerge da un loro lavoro pubblicato sul web.  Secondo la loro teoria questi dischi concentrici sono il segno di un universo ciclico eterno. Penrose spiega che l'inflazione non può spiegare lo stato di entropia molto basso in cui l'universo si pensa dovesse trovarsi all'inizio. Lui ed il suo co-autore, non credono che lo spazio ed il tempo hanno avuto inizio con il Big Bang, ma che invece, l'evento è stato soltanto uno tra tanti. Ogni "Big Bang" ha segnato l'inizio di una nuova era, ed il nostro universo è solo uno dei tanti universi ciclici, iniziando un nuovo universo al posto di quello di prima.

Purtroppo prima di essere certi di questi risultati c’e’ bisogno di misure della temperatura di fondo piu’ accurate che e’ proprio quello che sta facendo il satellite Planck con una risoluzione 3 volte maggiore di quella di WMAP. Con questa sensibilita’ dovrebbe essere possibile per gli scienziati individuare con certezza questi dischi concentrici rispetto al rumore di fondo.

L’eterna inflazione con la sua predizione del multiverso ci ricorda che i parametri che una volta si pensavano dover essere stati programmati esattamente al valore attuale, come Omega, possono essere spiegati da una teoria fisica piu’ fondamentale. E’ possibile che molte delle costanti i cui valori oggi non ci sappiamo spiegare potranno essere capite quando riusciremo ad arrivare ad una teoria del tutto o quando riusciremo a rivelare segnali di altri universi. Non ci resta che aspettare con fiducia.

 

Come le lenti gravitazionali ci mostrano la materia oscura.

Molti di voi avranno sentito parlare della curvatura della luce da parte di un corpo massiccio come una stella. Fu Einstein con l’introduzione della relativita’ generale ad ipotizzare cio’. Ma come puo’ la massa curvare i fotoni della luce che non hanno massa? In effetti e’ la curvatura dello spazio tempo generato dalla presenza di  una qualsiasi massa a curvare i raggi luminosi. Molti  di voi avranno visto l’immagine sottostante che rappresenta l’ammasso di galassie chiamato Abell Cluster 2218.

Se guardate attentamente noterete degli archi che altro non sono delle galassie di fondo che vengono distorte ed amplificate dal gigantesco ammasso di galassie Abell. Quando la luce che proviene da sorgenti piu’ lontane dell’ammasso passano nelle sue vicinanze subisce una deflessione che crea gli archi e i filamenti che vediamo.  Questo fenomeno e’ chiamato lente gravitazionale forte ed e’ uno degli spettacoli piu’ interessanti e belli dell’Universo. Sfortunatamente pero’ e’ un fenomeno molto raro. Infatti e’ molto difficile avere un allineamento tra la sorgente di luce e la massa che funziona da lente.

L’angolo di deflessione della luce verso la massa deflettente M e’ dato da:

dove G e’ la costante gravitazionale, r la distanza tra la massa M e il raggio di luce e c la velocita’ della luce. Questa semplice formula ci mostra come a partire dalla misura dell’angolo di deflessione dei raggi di luce e’ possibile risalire alla massa M del corpo deflettente.  

Oltre alle lenti gravitazionali forti esistono anche quelle che chiamiamo lenti gravitazionali deboli sicuramente meno spettacolari di quelle forti ma che come vedremo ritornano utili per mettere in evidenza la materia oscura. Come molti di voi sapranno, la materia visibile presente nell’universo e’ solo una piccola parte di quella necessaria per giustificare l’universo cosi come lo vediamo oggi. Dall’osservazione delle galassie a spirali si e’ visto che la velocita’ in funzione della distanza dal punto centrale della galassia si mantiene pressocche’ costante mentre tenendo conto della sola materia visibile la curva sarebbe stata quella tratteggiata in blu (curva A).

Per risolvere questo enigma gli astrofisici hanno ipotizzato la presenza nell’intero universo di materia non visibile, cioe’ materia che non emette luce ma che esercita un’attrazione gravitazionale sulla materia circostante. Ad oggi nessuno sa di cosa sia composta realmente questa materia oscura. Ci sono diverse ipotesi ma nessuna di esse ha trovato conferma nella realta’. Vediamo adesso come le lenti gravitazionali ci possono dare una mano nella comprensione della materia oscura.

Nell’immagine qui sopra e’ simulata una parte del nostro universo. In esso possono esserci delle regioni ricche di materia dove grazie all’azione della gravitazione questa comincia a formare degli ammassi. Ci sono altre regioni dove invece c’e’ assenza di materia e si formano dei grandi vuoti, chiamati voids. Quando la luce proveniente da sorgenti al di la’ di questi ammassi arriva ai nostri telescopi, essa non forma immagini spettacolari come quelle delle lenti gravitazionali forti; accade comunque un qualche cosa di molto interessante che noi possiamo studiare. Vediamo di cosa si tratta.

Supponiamo di avere delle sorgenti luminose di forma sferica distribuite a caso e supponiamo che non ci siano oggetti massivi tra esse e i nostri telescopi. Quello che vedremmo e’ un qualche cosa del genere.

Cosa succede se tra queste sorgenti e noi inseriamo un qualche oggetto massiccio? Ricordiamoci che siamo nell’ipotesi di assenza di lenti gravitazionali forti e quindi non ci aspettiamo di vedere archi, filamenti, o anelli.

I risultati di una simulazione mostrano comunque che le sorgenti di luce vengono distorte dall’effetto lente gravitazionale debole. Da sfere diventano degli ellissoidi piu’ o meno schiacciati. Bene. Tutto quello che dovremmo fare e’ misurare quanto ellettiche sono le galassie e da questo ricavare le masse presenti tra queste sorgenti e i nostri telescopi. Purtroppo le galassie reali hanno forme diverse tra loro e non sono delle sfere perfette come abbiamo supposto. Quando guardiamo gli oggetti nell’Universo abbiamo sempre l’effetto combinato di una debole distorsione dovuta all’effetto lente gravitazionale e dell’intrinseca ellitticita’ delle galassie (chiamato shape noise). Qui sotto una simulazione che fa vedere la differenza tra il caso con galassie suppooste sferiche (without shape noise) e quelle con forme diverse ( with shape noise).

Tipicamente l’ellitticita’ intrinseca e’ maggiore della distorsione gravitazionale. Ad ogni modo la misura di tante galassie puo’ essere combinata per mediare questo rumore. L’orientazione dell’ellitticita’ intrinseca delle galassie dovrebbe essere quasi tutta randomica cosi che l’allineamento sistematico tra galassie multiple generalmente si puo’ assumere essere causato dal solo effetto lente.  

Dalla misura dell’elletticita’ indotta dalla gravitazione e’ possibile risalire alla densita’ di materia visibile e non,  presente tra le sorgenti di luce e noi sulla Terra.  

Il confronto tra la distribuzione della materia oscura mappata con la tecnica del lensing debole, la distribuzione della materia visibile e quella dei raggi X rivela interessanti interconnessioni tra la materia oscura e i componenti delle stelle e dei gas.  Un esempio molto famoso e’ il cosiddetto Bullet Cluster che dista da noi circa 3,4 miliardi di anni luce. Quest’immagine e’ stata realizzata sovrapponendo alle galassie visibili nell’ottico, due nuvole di raggi X emesse da gas caldi e mostrate in rosso. Oltre alle masse visibili delle galassie e dei gas che emettono i raggi X c’e’ da aggiungere la materia oscura rappresentata come un alone blu. 

Gli astrofisici pensano che il Bullet Cluster si sia formato dallo scontro di due ammassi che hanno separato la materia oscura da quella barionica. L’osservazione dei raggi X mostra come la maggior parte della materia barionica del sistema e’ concentrata nel suo centro. Notare che la radiazione X e’ molto vicina al centro del sistema in quanto nel passare uno attraverso l’altro i due ammassi hanno rallentato le particelle di gas. Questo invece non e’ successo ai due aloni di materia oscura che risiedeva attorno ai due ammassi prima dello scontro e che e’ rimasta separata.

Da immagini come queste si e’ capito che la materia oscura non interagisce con la materia ordinaria ma contribuisce solo alla gravita’. La materia oscura non emette e non assorbe le radiazioni elettromagnetiche  e quindi non puo’ essere vista con i telescopi. Essa costituisce il 23% della materia presente nell’universo mentre solo il 4,6% e’ dovuto alla materia ordinaria e il rimanente 72% alla cosiddetta energia oscura responsabile dell’accelerazione attuale dell’universo. La quantita’ di materia presente nell’universo non e’ sempre stata costante. La sua percentuale era molto piu’ alta dopo 380000 anni dal big bang quando la radiazione finalmente non venne piu’ assorbita dagli elettroni e l’universo usci’ dal suo stato di opacita’ completa.  

In definitiva per sapere quanta massa c’e’ in un ammasso, e dove si trova questa massa, tutto quello che dobbiamo fare e’ misurare le sorgenti di luce che si trovano al di la dell’ammasso e fare entrare in gioco l’effetto lente gravitazionale debole. Tutto qui.

Chi e’ nato prima: la galassia o il buco nero?

Un buco nero e’ un oggetto massivo che esercita un’attrazione gravitazionale cosi intensa da impedire alla materia e alla luce di fuggire via da esso: in questo senso e’ nero. In esso la materia e’ addensata in un piccolo punto (singolarita’) e questa determina il raggio di una superficie immaginaria detto raggio di Schwarzschild. Per esempio un buco nero di massa pari a quella del Sole avrebbe un raggio di circa 3 Km mentre per una massa pari a quella della Terra il raggio sarebbe di un solo centrimetro.

Un buco nero essenzialmente e’ il frutto di una forte distorsione dello spazio-tempo dovuta alla presenza di un forte campo gravitazionale. La superficie di un buco nero, chiamata orizzonte, e’ una superficie di separazione chiusa entro la quale la velocita’ di fuga e’ maggiore della velocita’ della luce. Un risultato notevole e’ che l’interno di un buco nero non ha relazione causale con il resto dell’universo: nessun processo fisico che avvenga all’interno dell’orizzonte degli eventi puo’ comunicare la propria esistenza o i propri effetti all’esterno. Secondo la relativita’generale di Einstein, lo spazio e il tempo sono deformati dal campo gravitazionale dovuto ai corpi dotati di massa e la deformazione e’ piu’ forte in prossimita’ di un buco nero. Buchi neri di massa stellare si ritiene si formino quando stelle massiccie (dell’ordine di 30 masse solari e piu’) subiscono il collasso gravitazionale ed esplodono come supernove.

E’ opinione comune tra gli astronomi che nel nucleo di tutte le galassie sia presente un buco nero di massa compresa tra 1000000 e 1000000000 masse solari. Questi buchi neri vengono indicati come supermassivi. Le principali evidenze osservative della presenza di questi buchi neri sono:

·         L’attivita’ presente nei nuclei di alcune galassie quali i quasar e galassie Seyfert

·         La dinamica del materiale che orbita nelle regioni centrali delle galassie

Le prime galassie attive scoperte furono i quasar. Fin dall’inizio si era capito come essi fossero estremamante luminosi. L’unico meccanismo che riesce a generare una simile luminosita’ e’ l’accrescimento di materia da parte di un buco nero. Lo studio dei quasar mostra come in passato fossero molto piu’ abbondanti di adesso. L’evoluzione della luminosita’ dei quasar e’ spiegata col fatto che con il tempo i buchi neri supermassivi al centro delle galassie fagocitavano sempre piu’ materia con conseguente aumento della luminosita’. Una volta esaurito il materiale intorno al buco nero il nucleo della galassia diventa quiescente.

Ma questi buchi neri erano supermassivi fin dalla nascita? Secondo la comunita’ scientifica no. Essi sono cresciuti in dimensione grazie al gas e stelle presenti nelle galassie ospiti nei primi anni di nascita dell’universo. Questi risultati vengono dall’analisi fatta dalla Nasa col telescopio Hubble che ha studiato piu’ di 30 galassie. I risultati sono sommarizzati nelle immagine sottostanti dove e’ possibile vedere che piu’ il bulge (il nucleo centrale) di una galassia e’ grande in massa e piu’ e’ massiccio il buco nero ospite.

Questi dati sembrano favorire l’idea che un buco nero supermassivo non abbia preceduto la nascita della galassia ospite ma che invece si sono evoluti insieme intrappolando tanto piu’ materiale quanto piu’ il bulge della galassia era massiccio. E i quasars altro non sono che le emissione energetiche della materia catturata dai buchi neri supermassivi al centro delle galassie. In questo modo abbiamo dato una spiegazione ai centri galattici attivi, i buchi neri, e i quasars. Sono tutti intercorrelati tra di loro ed una solo teoria riesce a spiegare il tutto.

Ma siamo proprio sicuri che i buchi neri e le galassie nascono ed evolvono insieme? Due studi autorevoli sembrano indicare di no.

Il primo e’ di un gruppo di astronomi della Virginia che hanno scoperto un buco nero supermassivo in una galassia nana chiamata Henize 2-10, che si trova in una fase di formazione stellare. Questa scoperta avvenuta per caso ha delle importanti implicazioni sulla comprensione dell’evoluzione delle galassie e del loro buco nero centrale. In particolare questa scoperta suggerisce che i buchi neri supermassivi possono svilupparsi prima della crescita della loro galassia ospite.

L’altro studio e’ qello realizzato all’universita’dell’Ohio dove sono stati analizzati quasars apparsi qualche miliardo di anni dopo il big bang. Anche se questi quasars erano ovviamente giovani contenevano tante stelle in formazione come anche un buco nero supermassivo completamente formato. Il numero di quasars analizzati e’ stato dell’ordine delle centinaia. Anche la piu’ piccola e piu’ quiescente delle galassie attive conteneva un buco nero dell’ordine dei 100 milioni di volte il nostro sole. Da un punto di vista teorico questi buchi neri avrebbero richiesto dei tempi lunghissimi per diventare cosi’ grandi se essi fossero nati come un piccolo seme insieme alla galassia ospite.

La questione non e’ ancora completamente risolta e ulteriori conferme saranno necessarie anche se al momento tutto sembra confermare che i buchi neri sono nati prima delle galassie e che la loro immensa gravita’ attirando gas, polveri e stelle abbiano dato il via alla nascita delle galassie.   

La matematica delle api

La scienza è la poesia della realtà come afferma lo scienziato Richard Dawkins etologo ed evoluzionista. E in particolare la matematica è alla base della natura e di molte sue costruzioni che possiamo considerare artistiche. Non a caso Galileo Galilei  diceva a proposito dell’Universo: “Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro labirinto” Il Saggiatore, Galileo Galilei (1564-1642).

Come riportato ampiamente nel mio libro “ L'Universo dei numeri i numeri dell'Universo" i giovani di oggi non amano la matematica. Essi la ritengono qualcosa di artificioso, estraneo, senza legami con la natura, con l’arte, la musica, la letteratura; difficile da capire, piena di formule strane che non hanno niente a che fare col mondo che ci circonda. Nel mio libro ho provato a smentire queste false opinioni andando a curiosare nell’intero Universo con occhi matematici, cercando tra i fiori e le foglie, le pigne e le spiraleggianti galassie, tra le cicale e le lenti gravitazionali la presenza della regina delle scienze. Voglio continuare con questo mio proposito descrivendovi in questo post come le api mostrano di conoscere la matematica e la geometria meglio di molti nostri giovani studenti. Come ci riescano pero’ rimane un mistero.

Cominciamo con il chiederci come mai le cellette del favo hanno tutte una sezione di forma esagonale. La risposta come sempre ce la da’ la matematica. Gli esagoni regolari, cioe’ esagoni con tutti i lati uguali e gli angoli uguali (120 gradi), fanno parte delle famiglia dei poligoni regolari con cui e’ possibile tassellare completamente il piano, cioe’ ricoprirlo completamente senza lasciare spazi vuoti. Oltre all’esagono lo puo’ fare il triangolo equilatero e un quadrato.    

Ma allora perche’ le api usano proprio l’esagono? Per poter ricoprire il piano con dei triangoli equilateri bisogna fare in modo che 6 di essi abbiano in comune un vertice (in questo modo essendo l’angolo di ogni triangolo equilatero di 60 gradi avremo che 6*60 fa l’angolo giro). Per i quadrati invece ne avremo 4 che condividono lo stesso vertice (4*90=360 gradi) e per l’esagono 3 (6*120=360 gradi). La differenza significativa sta quindi nel perimetro complessivo della struttura. Le api scelgono quella piu’ economica da un punto di vista della cera utilizzata. Meno perimetro meno cera. Si tratta di un problema di minimo. Calcoliamo il perimetro di un triangolo equilatero, di un quadrato e di un esagono a parita’ di area. Supponiamo che la superfice sia uguale a 1 (A=1) e indichiamo con Lt, Pt, Lq, Pq, Le, Pe, lati e perimetri del triangolo, quadrato ed esagono rispettivamente.

Per il quadrato abbiamo:

Per il triangolo equilatero calcoliamo prima l’altezza utilizzando il teorema di Pitagora:

da cui deriva che l’area e il perimetro sono uguali a:

Per l’ esagono, essendo costituito da 6 triangoli equilateri avremo:

Si puo’ osservare che a parita’ di superficie, il perimetro piu’ piccolo e’ quello dell’esagono. Ecco perche’ le api lo hanno scelto per la costruzione del favo. E’ la struttura che richiede meno cera per la sua costruzione. Per essere precisi, il cerchio e’ la figura geometrica che a parita’ di superficie ha il perimetro piu’ piccolo (P=3.544) ma le api non lo utilizzano perche’ se e’ vero che richiede meno cera e allo stesso tempo lascia troppi spazi vuoti inutilizzabili cioe’ non permette la tassellazione del piano.



Le api tutti i giorni costruiscono i loro favi seguendo una procedura matematica che ottimizza lo spazio anche se non conoscono le leggi matematiche. Possiamo pensare che esse sanno fare matematica anche se in modo inconsapevole cioe’ senza rendersene conto. E’ probabile che l’artefice di tutto cio’ sia la selezione naturale in azione da millenni sul nostro pianeta che non fa altro che scegliere le opzioni migliori in termini di sopravvivenza.

Passiamo adesso ad un secondo problema matematico che le api sembrano saper risolvere anche piu’ velocemente di un computer. Si tratta del cosiddetto problema del commesso viaggiatore.  

Data per esempio una rete di città disposte in modo sparso e connesse da strade, si tratta di trovare il percorso più breve che un viaggiatore deve coprire per visitare tutte le città una sola volta. Il problema a prima vista puo’ sembrare facile, ma in effetti lo e’ solo se il numero delle citta’ e’ molto piccolo. In caso contrario anche dei grandi computer possono avere delle difficolta’ ad identificare il percorso minimo in quanto non esiste un algoritmo efficiente e quindi non resta che lavorare di forza bruta calcolando tutti i possibili perscorsi e scegliendo poi quello piu’ breve. E questo puo’ avere delle ripercussioni nel mondo reale visto che il problema del commesso viaggiatore trova applicazioni pratiche nell’organizzazione della logistica e dei trasporti, nel disegno di circuiti integrati e nella robotica industriale. Per una mente umana sarebbe difficile, e richiederebbe molto tempo, elaborare N nodi e risolvere il problema; per un computer invece l'elaborazione dei dati risulta più veloce, ma si fatica lo stesso con numeri superiori ai 1000 nodi. Alle api, invece, la soluzione del problema del commesso viaggiatore viene del tutto naturale.
Alcuni scienziati della Queen Mary School e della Royal Halloway University infatti, hanno scoperto che le api imparano velocemente a trovare il tragitto piu’ breve che separa i fiori da cui prelevano il nettare, anche se i fiori sono stati scoperti dalle api seguendo un  tragitto diverso da quello ottimale.   
"In natura, le api devono collegare centinaia di fiori con un metodo che minimizzi le distanze, per poi trovare in modo affidabile la via di casa, non è di certo un'abilità banale se si ha il cervello delle dimensioni di una capocchia di spillo!" dice Lars Chittka della Queen Mary's School of Biological and Chemical Sciences. "Di sicuro questi problemi tengono i supercomputer impegnati per giorni. Studiando come i cervelli delle api risolvono queste sfide potrebbe consentirci di identificare il circuito neurale minimo per risolvere problemi complessi".

Il team di ricerca ha utilizzato dei fiori artificiali controllati da computers, per verificare se le api seguissero un cammino definito dall'ordine con cui hanno scoperto i fiori, o se fossero in grado di trovare il tragitto più corto. Dopo aver esplorato i fiori artificiali, le api hanno presto appreso a volare seguendo il percorso più breve.

La scoperta non ha rilevanza soltanto per l'informatica. Potrebbe infatti fornirci informazioni utili per migliorare le nostre infrastrutture dei trasporti e migliorare Internet attraverso l'apprendimento di come le informazioni fluiscano attraverso i nodi della Rete. Il tutto senza l'utilizzo di computers.
"C'è una percezione comune, che cervelli più piccoli costringano gli animali ad essere semplici" dice Mathieu Lihoreau, co-autore della ricerca. "Ma il nostro lavoro con le api mostra capacità cognitive avanzate con un numero davvero limitato di neuroni. C'è un bisogno urgente di comprendere il sistema neuronale che sta alla base dell'intelligenza animale, e sistemi nervosi relativamente semplici come quelli delle api rendono la soluzione del mistero più alla portata". Alcuni mesi fa il team del Queen Mary School non solo ha confermato la capacita’ delle api di risolvere il problema del commesso viaggiatore ma addirittura ha messo in evidenza la loro capacita’ di ottimizzare sia la distanza che la quantita’ di nettare disponibile in ogni fiore. Quando tutti i fiori usati nell’esperimento (sempre artificiali) contengono la stessa quantita’ di nettare, le api imparano a volare lungo la traiettoria piu’ corta per visitarli tutti. Ma se un fiore contiene piu’ nettare di un altro, questo forza le api a decidere se seguire la strada piu’ corta o se visitare per primo il fiore che da’ la ricompensa maggiore.

Quello che l’esperimento ha mostrato e’ che le api decidono di visitare per primo il fiore che contiene piu’ nettare se questo non implica un significativo aumento della distanza totale; in caso contrario le api non visitano questo fiore per primo. Questo comportamento rivela che le api riescono a fare un giusto trade-off tra la minima distanza e la quantita’ di nettare disponibile. E’ la prima evidenza che gli animali per procurarsi il cibo, usano una memoria combinata della locazione e della sua profittabilita’ quando decide quale strada seguire.

Come ultimo esempio voglio riportare i risultati di un esperimento di un team del Vision Centre in Australia che mostrano come le api possono distinguere i numeri osservandoli.  Nel disegno riportato qui sotto viene schematizzato l’esperimento fatto. L’ape incontra una porta sulle cui pareti sono disegnati dei pallini neri e attraversa un tunnel di un metro. Alla fine di questo tunnel c’e’ un deflettore all’interno di quella che viene chiamata la camera della decisione. All’interno di questa camera puo’ scegliere due strade C1 e C2. Una sola di queste due camere all’interno ha una ricompensa (una soluzione di zucchero) ed essa viene indicata con lo stesso numero di punti neri  presenti in S. Chiaramente se l’ape sceglie la camera che ha lo stesso numero in ingresso avra’ una ricompensa altrimenti no.

I risultati hanno dimostrato che le api possono distinguere un pattern a 2 e 3 punti senza dover contare I punti. E con un po’ di insegnamento possono imparare la differenza anche tra 3 e 4 punti. Comunque a 4 la matematica delle api sembra arrestarsi. Oltre non riescono ad andare, nel senso che non riescono a distinguere 4 da 5. I risultati sono indipendenti dal pattern utilizzato, dal colore e dalla forma dei punti. Le api riconoscono la differenza tra due, tre e quattro, sebbene con minore affidabilita’ il 4.Questo processo va sotto il nome di “subitizing”, che significa che le api possono rispondere rapidamente ad un piccolo numero di oggetti. Ci sono state diverse evidenze che I vertebrati, come piccioni, delfini o scimmie, hanno delle competenze numeriche, ma mai ci si sarebbe aspettato di trovare le stesse abilita’ negli insetti. Il team del Vision centre crede che molto probabilmente non c’e’ alcuna frontiera tra gli insetti, animali e noi.  La questione piu’ interessante e’ se le api possono realmente eseguire dei calcoli semplici di aritmetica e a questo scopo il team di studiosi capitanato dal  Dr. Shaowu gia’ pronto per eseguire un esperimento per esplorare cio’. Non ci resta che aspettare. Chi e’ disposto ancora a credere che la matematica e’ quella disciplina noiosa, fredda e piena di formule che non ha nessun legame con la realta’?