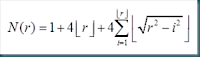Sicuramente sara’ capitato a molti di voi che amano la matematica di imbattersi almeno una volta nel sito del Dr.
Neil Sloane dei Laboratori AT&T del New Jersey in America. Si tratta del piu’ grande data base di numeri esistente al mondo. Si chiama “On line Encyclopedia of Integer Sequences” con circa 200.000 sequenze numeriche. Questo l’indirizzo
web. Una sequenza e’ una lista di numeri, eventualmente infinita, che puo’ essere calcolata utilizzando delle semplici regole.
La sequenza piu’ famosa e’ sicuramente quella di Fibonacci dove ogni termine e’ dato dalla somma dei due termini precedenti: 1, 1, 2, 3, 5, 8, 13, 21, 34,.....
Il Dr. Sloane ha lavorato a questa enciclopedia per circa 40 anni ed oggi e’ consultata gratuitamente tramite il web da diversi scienziati nel mondo. Gli astronomi, per esempio, che cercano possibili vite extra-terresti analizzando i segnali radio che arrivano dall’Universo, la consultano per capire se si tratta di una sequenza casuale o no.
Essa aiuta anche le compagnie di telefoni mobili quando cercano di eliminare le interferenza tra diverse chiamate. In effetti, quando facciamo una chiamata, ci viene assegnata una certa frequenza che non deve interferire con quelle di altre persone.
Frequenze basate su sequenze di numeri che non si ripetono mai, individuabili grazie al data base di Sloane, garantiscono al cliente l’assenza di disturbi di interferenza.
Un altro aiuto viene dato agli esperti di crittografia che utilizzano la fattorizzazione dei numeri primi per trasmettere messaggi segreti.
All’interno di questo grande contenitore online, si possono trovare successioni di numeri di diverso tipo. Da quelle semplici a quelle difficili da calcolare, da quelle ordinate a quelle disordinate, da quelle basate sul calcolo combinatorio a quelle ricreazionali. Anche io negli anni passati ho dato un piccolo contributo a questa enciclopedia inserendo alcune mie sequenze che potete consultare a questo link.
Neil Sloane ha una lista di quelle che lui ritiene le sue favorite. Vediamo quali sono.
La prima e’ la sequenza di Recaman, che inizia come la sequenza di Fibonacci per poi diventare significativamente diversa. Questa sequenza e’ molto difficile da analizzare in quanto non mostra alcuna regolarita’, non aumenta, non diminuisce e ne’ oscilla in modo regolare.
Se provassimo a graficare i numeri di Fibonacci, questi crescerebbero in modo prevedibile, con una velocita’ ben determinata. La sequenza di Recaman, invece, barcolla come un ubriaco, andando su e giu’ in modo del tutto casuale. Il suo grafico assomiglia allo scarabocchio di un bambino.
La regola alla base e’ molto semplice:
Supponendo di partire con 1, si ottiene facilmente:
1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, .......
Nel database di Sloane, in genere, le sequenze che dipendono dalla scelta della base non vengono mantenute anche se ci sono delle eccezioni. Partiamo, per esempio, con un numero n; se esso e’ palindromo (cioe’ se si legge allo stesso modo da sinistra a destra e viceversa, come 121, 25652...) ci fermiamo; altrimenti aggiungiamo il numero n a se stesso con le cifre al contrario. Ripetiamo questa operazione fino a quando non raggiungiamo un numero palindromo, oppure assegniamo -1 se non lo raggiungeremo mai. Partendo con 19, otteniamo:
19 –> 19+91=110 –>110+011=121
che e’ un palindromo, e quindi ci fermiamo e il diciannovesimo termine della sequenza sara’ 121. La sequenza inizia con:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11, 33, 44, 55, 66, 77, 88, 99, 121, 22, 33, 22, 55, 66, 77, . . . .
E se partiamo col numero 196 cosa succede?. In questo caso otteniamo:
196, 887, 1675, 7436, 13783, 52514, 94039, 187088, 1067869, 10755470, 18211171, . . . .
che sembra non raggiungere mai un numero palindromo. Sarebbe interessante avere una dimostrazione di cio’, ma al momento non esiste. Questo e’ uno di quei problemi che sembrano troppo difficili da risolvere per la matematica del XXI secolo.
Un’altra sequenza molto amata da Sloane, e’ quella chiamata “Powertrains” . In questo caso ogni termine della sequenza e’ legato al numero di passaggi necessari per arrivare ad un numero ad una sola cifra partendo da un numero qualsiasi n e moltiplicando tra loro le sue cifre. Partendo con 679, per esempio, sono necessari 5 passaggi per arrivare a 6:
679 –> 378 –> 168 –> 48 –> 32 –>6
Il numero di passaggi e’ chiamato la persistenza del numero; nel caso di 679 la persistenza e’ uguale a 5. I piu’ piccoli numeri naturali con persistenza 1,2,3,4,.... sono dati dalla sequenza:
10, 25, 39, 77, 679, 6788, 68889, 2677889, 26888999, 3778888999, 277777788888899
Sloane, in un articolo del 1973 ha congetturato che questa sequenza e’ finita e fino ad oggi non e’ stato trovato nessun numero naturale con persistenza maggiore di 11.
Tutti sono invitati alla ricerca. Qualcuno dei lettori potrebbe scontrarsi con un numero n con persistenza maggiore di 11 ed entrare nel guinness dei primati della matematica.
Nel 2007, John Conway, l’autore del gioco della Vita, ha proposto una variazione al concetto di persistenza suggerendo di considerare nel caso in cui un numero n ha un’espansione decimale del tipo abcd..., il numero abcd.... che termina in un esponente o una base a seconda che il numero di cifre contenute in n e’ pari o dispari. Si assume che 00 sia uguale ad 1. Questa sequenza comincia con:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 1, 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1, 5, 25, 125, 625, 3125, 15625,…
e il suo grafico e’ mostrato in figura 1.
Figura1: Rappresentazione della sequenza powertrain. Sull’asse y e’ riportato il logaritmo di ogni termine della sequenza piu’ uno.
Se consideriamo la mappa n à Powertrain(n) ci accorgiamo che alcuni punti sono dei punti fissi (o attrattori) come per esempio 2592 essendo 25·34 = 2592 –> 25·92 = 2592. La successione degli attrattori del Powertrain e’ data da:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 2592, 24547284284866560000000000
e Sloane ha congetturato che non ci sono altri termini. Di sicuro questo e’ vero per 10100 in quanto e’ stato verificato con una ricerca esaustiva al computer. Ancora una volta regole molto semplici possono dar origine a questioni che potrebbero rimanere senza una risposta per secoli.
Un altra sequenza interessante, che solleva un problema veramente difficile da risolvere e’ la cosiddetta sequenza di Lagarias, definita come:
dove H(n) e’ l’ennesimo numero armonico dato da:
e σ(n) la somma dei divisori di n (per esempio σ(6)=12 in quanto i divisori di 6 sono 1, 2, 3, 6). I primi termini sono riportati nell’ enciclopedia di Sloane e sono:
0, 0, 1, 0, 4, 0, 7, 2, 7, 5, 13, 0, 17, 9, 12, 8, 23, 5, 27, 8, 21, 20, 34, 1, 33, 25, . . .
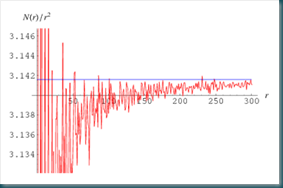
Jeff Lagarias, da cui la sequenza prende il nome, nel 2001 ha dimostrato che se a(n) e’ sempre maggiore o uguale a zero, questo equivale a dire che la famosa ipotesi di Riemann, e’ vera. In figura 2, viene mostrata un’immagine dell’andamento di questa sequenza per diversi valori di n.
Figura2: Rappresentazione della sequenza di Lagarias.
Continuiamo il nostro viaggio e vediamo quale e’ il nostro prossimo incontro. Si tratta della cosiddetta sequenza EKG. I primi due termini sono 1 e 2, e i termini successivi vengono calcolati considerando il numero positivo piu’ piccolo non presente gia’ nella successione e che ha un fattore comune non banale con il termine precedente. Poiche’ a(2)=2, allora a(3) deve essere pari, ed e’ quindi uguale a 4. a(4) deve avere un fattore comune con 4 e quindi non puo’ che essere uguale a 6. Il piu’ piccolo numero non presente nella sequenza e che ha un fattore in comune con 6 e’ 3, cosicche’ a(5)=3 e cosi’ via. I primi 18 termini di questa successione sono:
1, 2, 4, 6, 3, 9, 12, 8, 10, 5, 15, 18, 14, 7, 21, 24, 16, 20……..
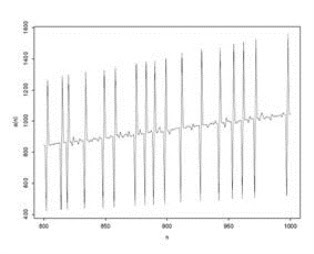
E’ chiaro che se nella sequenza compare un numeri primo p, allora il termine immediatamente precedente o immediatamente successivo sara’ uguale a 2p. Inoltre, Lagarias, Rains e Sloane hanno notato che ogni numero primo p e’ sempre preceduto da 2p e seguito da 3p. Questo e’ stato provato essere vero per i primi 10.000.000 termini della successione. Ma non sono riusciti a trovare una dimostrazione di cio’. Ancora un altro problema aperto su cui potersi cimentare. La sequenza e’ stata chiamata EKG in quanto essa assomiglia ad un elettrocardiogramma quando riportata su grafico come mostrato in figura3.
Figura3: I primi 100 termini della sequenza EKG sopra, e i termini da 800 a 1000 sotto.
Sebbene i primi termini di questa sequenza sembrano ondeggiare, se grafichiamo gli stessi termini della figura 3, senza unire i punti tra di loro con delle linee, otteniamo l’immagine della figura 4.
Figura4: I primi 1000 termini della sequenza EKG senza unire i punti successivi.
Si puo’ vedere come i valori della sequenza si raggruppano lungo tre linee quasi rette. Questo e’ un comportamento simile a quello dei numeri primi, che inizialmente sembrano imprevedibili, per poi tendere sempre piu’ ad una curva data da ~n·ln(n). C’e’ una precisa congettura per quanto riguarda le tre rette della figura 4, che stabilisce che la maggior parte dei valori della sequenza EKG si stabilizzano intorno alla linea a(n)~n(1+1/(3ln(3)) centrale, ed occasionalmente solo quando a(n)=p, cioe’ in corrispondenza dei numeri primi, vengono prodotti i punti della linea al di sopra a(n)=3p e al di sotto a(n)=p di quella centrale. E’ stato dimostrato che la sequenza ha essenzialmente una crescita lineare nel senso che esistono due costanti c1 e c2 tali che c1n<a(n)<c2n per tutti i valori di n. Questo e’ tutto quello che si conosce sulla sequenza EKG. Come si intuisce c’e’ ancora tanto lavoro da fare.
E non finisce qui. La prossima sequenza non e’ da meno dell’EKG. Semplice da definire ma difficile da analizzare e tante questioni ancora aperte su cui poter lavorare. Si tratta del problema del quadrato approssimato. Prima di tutto indichiamo col simbolo I(x), il piu’ piccolo intero maggiore o uguale a x. Se partiamo con qualsiasi frazione piu’ grande di 1, come per esempio 8/7, e applichiamo continuamente il prodotto x·I(x) e’ possibile arrivare ad un numero intero.
Poiche’ 8/7=1.142.., I(8/7)=2 e quindi x·I(x)=16/7. Riapplicando lo stesso procedimento alla frazione 16/7 si ottiene 48/7 e poi 48. Per arrivare ad un numero intero sono stati necessari 3 passaggi. La questione che sorge e’: per qualsiasi frazione iniziale, e’ sempre possibile raggiungere un numero intero? Lagarias e Sloane, in un articolo pubblicato sul giornale Experimental Math del 2004, hanno mostrato che quasi tutte le frazioni maggiori di 1 raggiungono un numero intero, e che se il denominatore e’ uguale a 2 allora tutte le frazioni maggiori di 1 raggiungono un numero intero. Comunque una prova completa ancora non esiste. Il problema ha delle similitudini con quello di Collatz che abbiamo analizzato in uno dei post precedenti, e questo spiega la difficolta’ nel risolverlo.
I numeri coinvolti sono numeri che crescono velocemente. Se partiamo dalla frazione 6/5, per esempio, l’applicazione successiva del prodotto x·I(x), genera la sequenza:
che raggiunge un numero intero con 57735 cifre, dopo 18 passaggi. Se la frazione iniziale ha il denominatore uguale a 2, allora e’ possibile determinare in quanti passaggi si raggiunge un numero intero. Ma se il denominatore e’ gia’ uguale a 3, non sappiamo cosa accade.
Partendo con frazioni della forma (k+1)/k, con k un qualsiasi numero intero, sembra necessario un numero di passaggi veramente lungo primo di approdare ad un numero intero. E’ divertente notare che se k=199, la frazione 200/199 raggiunge un numero intero enorme, approssimativamente uguale a :
cioe’ un numero con circa 10435 cifre. Diversamente da quanto credono la maggior parte delle persone molta della matematica utilizzata per puri scopi teorici, trova poi applicazione nel mondo di tutti i giorni. E’ il caso del classico problema della “dissezione” che e’ stato applicato con successo nel campo delle comunicazioni ottiche.
Dato un poligono con n lati, e’ sempre possibile tagliarlo in un numero finito di pezzi che possono essere arrangiati, senza essere sovrapposti, a formare un quadrato della stessa area.
Ma qual’e’ il minimo numero d(n) di pezzi richiesti?
Per il caso n=3, quello che cerchiamo e’ il minimo numero di pezzi in cui e’ possibile dividere un triangolo equilatero in un quadrato. Al momento il numero minimo conosciuto e’ 4, come mostrato da Dudeney nel 1902 (vedi figura 5). E’ improbabile che si possa fare meglio di cosi ma fino ad oggi nessuno e’ riuscito a provarlo.
Figura5: Un triangolo puo’ essere dissezionato in 4 pezzi che possono poi essere arrangiati a formare un quadrato con la stessa area del triangolo.
Nessuno conosce con certezza i valori di d(n), eccetto chiaramente d(4) che e’ uguale a 1. Si conoscono solo i limiti superiori riportati come sempre nel sito web di Sloane:
4, 1, 6, 5, 7, 5, 9, 7,….
Qualcuno vuole tentare ad abbassare questi limiti?
Esistono altre due sequenze che nascono da due problemi di analisi combinatoria molto interessanti. Il primo si chiama il problema dei “meandri” e il secondo il problema dei “francobolli”. Entrambe queste sequenze di numeri, sono fondamentali, facilmente descrivibili, compaiono in diverse parti della matematica e sono complicate da calcolare.
Nel caso dei francobolli la questione e’ la seguente.
Consideriamo una striscia di francobolli, come mostrato in figura 6. Ci sono n francobolli numerati con 1,2,3,4...n a partire dalla sinistra e ognuno di essi ha una faccia superiore in verde e una faccia inferiore in nero. Tra due francobolli c’e’ una piccola striscia perforata (colore viola nella figura) che facilita la divisione dei francobolli.
Figura6: Striscia di francobolli.
Una tale striscia di francobolli puo’ essere piegata lungo le perforazioni in diversi modi per creare una pila di n francobolli. Assumiamo che le perforazioni siano perfettamente elastiche e quindi possano essere stirate a qualsiasi distanza. Quanti modi diversi esistono per piegare una tale striscia?
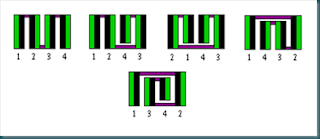
Di seguito viene riportato l’esempio di tutti i possibili piegamenti che si possono ottenere con 4 francobolli.
Alcuni di queste configurazioni sono quasi identiche ad altre, come per esempio, 1234 e 4321. Con lo scopo di rimuovere alcune delle simmetrie, e’ possibile restringere gli orientamenti a quelli in cui il primo francobollo nella sequenza ha il valore piu’ basso dell’ultimo. In questo modo 1234 sara’ permesso mentre 4321 no. Qui sotto viene mostrato il diagramma dei possibili piegamenti dei francobolli con lunghezza 4 rimuovendo le sequenze non permesse. Ci sono esattamente la meta’ degli oggetti del caso precedente.
Comunque in questo diagramma, ancora esiste un altro tipo di simmetria come quella tra 3214 e 1432. Rimuovendo anche questo tipo di simmetria quello che rimane e’ riportato nell’immagine che segue.
In definitiva la sequenza e’ data da:
1, 1, 2, 5, 14, 38, 120, 353, 1148, 3527, ……
L’altra sequenza, quella dei meandri parte dalla questione: in quanti modi diversi un fiume che scorre da SE a NE, attraversa una strada n volte?
Per n=5 ci sono 8 modi diversi di attraversamento come mostrato nello schema sottostante.
I termini di questa sequenza sono:
1, 1, 2, 3, 8, 14, 42, 81, 262, 538, 1828, ….
Anche se non sono state passate in rassegna tutte le sequenze favorite di Sloane, ci fermiamo qui invitando il lettore interessato a visitare il sito online, a proporre nuove sequenze e a lavorare sui quesiti ancora aperti. Ottima palestra per chi vuole mantenere allenato il proprio cervello.