3.14 la costante universale

 

 

La costante π appare un po’ ovunque; nella matematica e nella fisica, nella geometria come pure nella  statistica. In geometria  π viene definito come il rapporto tra la circonferenza e il diametro di un cerchio. Contrariamente al pensiero comune, π non è una costante fisica o naturale, quanto piuttosto una costante matematica definita in modo astratto, indipendente dalle misure di carattere fisico. Le prime 64 cifre decimali di π sono:

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 592

π è un numero irrazionale, cioè non puo’ essere scritto come quoziente di due interi. Questo è stato provato nel 1761 da Johann Heinrich Lambert. Inoltre, è un numero trascendente (ovvero non è un numero algebrico): questo fatto è stato provato da Ferdinand von Lindemann nel 1882 e significa che non ci sono polinomi con coefficienti interi o razionali di cui π è radice. Di conseguenza, è impossibile esprimere π usando un numero finito di interi, di frazioni e delle loro radici.

Questo risultato stabilisce a fortiori l'impossibilità della quadratura del cerchio, cioè la costruzione, con sola riga e compasso, di un quadrato della stessa area di un dato cerchio. Il valore di pi, e’ un vero numero irrazionale, nel senso che il suo sviluppo decimale non ha mai fine come può essere visto meglio scrivendo pi greco come sviluppo in termini di frazioni:

4(1/1 - 1/3 + 1/5 - 1/7 + 1/9 - ...)

Per i matematici la natura infinita di tale costante, significa che non c’e’ una relazione esatta tra la circonferenza di un cerchio e il suo raggio. La natura infinita comunque non e’ la cosa più interessante di pi greco. Lo e’  invece la sua universalita’,  cioe’ la presenza di tale costante nei posti più impensabili.

Nonostante sia un numero irrazionale, esso può essere usato per descrivere molti aspetti fondamentali del mondo che ci circonda. Per esempio, il Prof. Hans-Henrik Stolum dell’Università’ di Cambridge, ha calcolato per diversi fiumi in diverse zone geografiche il rapporto tra la reale lunghezza del fiume (seguendo cioe’ la sua traiettoria) e la distanza in linea d’aria. E cosa ha trovato? Esattamente pi greco.

Einstein scoprì che pi greco era un elemento cruciale nelle sue equazioni di Relatività Generale come anche nella sua “costante cosmologica” che sviluppò quando era avanti con gli anni e che definì come la forza che previene l’espansione dell’Universo. Nella teoria della relativita’ generale la forza di gravita’ esercitata da un corpo viene interpretata come la deformazione (curvatura) dello spazio tempo in cui gli altri corpi si muovono. In termini matematici questo viene espresso sinteticamente dalle equazioni

Gµν + Λgµν = 8 πGTµν  

dove il primo termine rappresenta la geometria dello spazio-tempo, il termine a destra del segno uguale il contenuto di materia-energia e il secondo membro contiene la costante cosmologica indicata con Λ e responsabile secondo gli scienziati (e contrariamente a quanto pensava Einstein) dell’attuale accelerazione dell’universo. Ancora una volta pi greco fa la sua bella compara addirittura nelle equazioni che regolano l’intero universo.  

Heisenberg usò la costante pi greco nel suo famoso principio di incertezza in meccanica quantistica mentre Coulomb la usò nella sua legge della forza elettrica e Keplero nella sua terza legge del moto planetario.

Pi greco e’ stato trovato anche nel famosissimo insieme di Mandelbrot.

Questa immagine e’ ottenuta considerando l’insieme dei numeri complessi C (cioè numero del tipo x+iy con x e y numeri reali e i l’unita’  immaginaria) tali che la successione definita da:

z_n+1=z_n²+c            z_o=0

non e’ divergente (cioe’ non esplode all’infinito). L’insieme e’ un frattale  e, nonostante la semplicità della definizione, ha una forma molto complessa. Solo con l’avvento dei computer e’ stato possibile visualizzarlo in tutti i suoi dettagli. L'insieme deve il suo nome a Benoît Mandelbrot che nel 1975 nel suo libro Les Objects Fractals: Forme, Hazard et Dimension rese popolari i frattali. In questo libro Mandelbrot introdusse il termine frattale per descrivere alcuni oggetti matematici che sembravano avere un comportamento "caotico". Questo genere di fenomeni nasce dalla definizione di curve o insiemi tramite funzioni o algoritmi ricorsivi.

Nel 1991, Dave Boll, uno studente in scienza dei computer dell’Università’ del Colorado, stava cercando di convincere se stesso che la connessione tra il cardioide di Mandelbrot e il disco alla sua sinistra (vedi freccia rossa nella figura sottostante) avvenisse solo tramite un punto c=(-0.75,0). Non era preparato a quello che stava per presentarsi ai suoi occhi. Per verificare, effettivamente che la strozzatura dell’insieme fosse infinitamente sottile, stava verificando dopo quante iterazioni i punti della forma sfuggivano all’infinito.

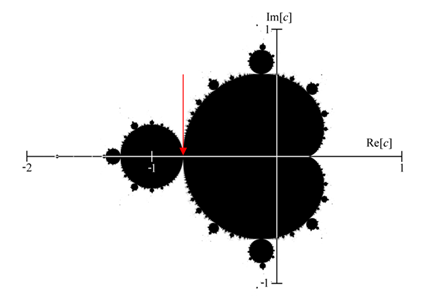
Nella tabella, il numero di iterazioni per diversi valori di epsilon (un numero molto piccolo per rappresentare la sottigliezza della strozzatura).

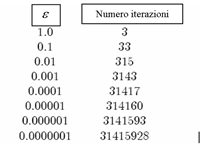
 Numero iterazioni per diversi valori di epsilon.

Se  consideriamo il prodotto di epsilon per il numero di iterazioni otteniamo quello che sorprese tanto Dave, e credo anche voi adesso, il tanto famigerato numero pi greco.

Nella scienza, in geografia e in astronomia, pi greco e’ un po’ ovunque, per qualche ragione che ancora sfugge ai matematici e agli scienziati, almeno fino ad oggi.

Ma spingiamoci oltre entrando in un campo che nulla a che fare con la scienza: cosa ha a che fare pi greco con i cerchi nel grano? Sembra che, se veramente esistono degli alieni nel profondo universo, questi conoscano la matematica ed in particolare il numero pi greco. Il primo Giugno del 2011 infatti, in Inghilterra vicino al Barbury Castle in Wiltshire e’ apparso un cerchio nel grano del diametro di 150 piedi che sembra rappresentare correttamente le prime 10 cifre di pi greco.

Guardando la figura, si può notare che i solchi nel grano a partire dal centro seguono una spirale verso l’esterno con vari punti in cui c’e’ un gradino. Questi sembrano manifestarsi con particolari angoli come si può vedere dall’immagine sotto a destra (il cerchio e’ diviso in 10 segmenti uguali con angoli di 36 gradi ciascuno).

Partendo dal centro, la prima sezione e’ larga 3 settori. Quindi c’e’ un gradino con al di sotto un piccolo cerchio nero che sta ad indicare il punto decimale. La sezione successiva e’ larga un solo settore e subito dopo c’e’ un altro gradino. La sezione successiva e’ larga 4 settori e cosi via fino a ritrovare il numero finale 3.141592654.

La decodifica e’ stata effettuata da un astrofisico in pensione, Michael Reed, che una volta scoperto il valore di pi greco fino alla decima cifra decimale ha annunciato: tutto questo mi lascia sbalordito. Non posso immaginare che tutto questo sia dovuto al caso.

Lucy Pringle, un’appassionata dei cerchi nel grano, ha affermato: e’ difficile pensare che un disegno cosi complicato possa essere stato creato da umani, tanto più che la notte precedente all’apparizione aveva piovuto nella zona e non sono state ritrovate tracce di fango tra i solchi del cerchio. E’ facile fare un tale disegno su un computer, ma provate a farlo di notte in un campo oscuro e a raggiungere la stessa accuratezza. Secondo Pringle, i cerchi nel grano si formano grazie a delle forze elettromagnetiche che colpiscono il suolo per alcuni nanosecondi. L’assessore della zona, Stewart Dobson, ha dichiarato: E’ difficile pensare che qualcuno abbia costruito manualmente questo disegno. O si tratta di una persona con buone conoscenze di matematica o si tratta di alieni con buona conoscenza della matematica.

Noi tendiamo a credere che, nel caso in cui gli alieni esistano davvero, essendo capaci di viaggiare per milioni di anni luce attraverso l’Universo, di sicuro conoscono pi greco. Nella figura sottostante un altro cerchio nel grano rappresentante l’insieme frattale di Julia.

Ritorniamo alla matematica del pi greco parlando adesso del suo sviluppo decimale. Il calcolo delle cifre decimali di pi greco ha affascinato i matematici fin dall’antichità’. Ludoph van Ceulen, spese la maggior parte della sua vita per calcolare le prime 35 cifre decimali. Non riuscì a vedere la pubblicazione del suo risultato e l’unica ricompensa fu l’iscrizione fatta dai suoi parenti sulla sua lapide.

Nel Dicembre del 2002, due scienziati del Canada, Ushio e Kuroda, utilizzando un potente computer, sono riusciti a calcolare, addirittura le prime (più di 1 trilione) di cifre decimali. La computazione ha impegnato il computer (Hitachi SR8000) per più di 600 ore.

Pickover, un ricercatore della IBM, in un suo recente libro ha riportato una rappresentazione digitale a matrice delle prime 1600 cifre decimali. Egli ha colorato in nero le celle contenenti una cifra decimale del pi greco dispari e in bianco quelle pari. A fianco viene anche riportata la matrice digitale del rapporto 22/7 che e’ un’approssimazione di pi greco. Si nota subito la differenza. La disposizione delle cifre decimali del rapporto 22/7 hanno un struttura (pattern) ben definita mentre quella del pi greco (a sinistra)  sembrano disporsi in modo completamente casuale.

Abbiamo provato a fare una cosa analoga usando 10 diversi colori, uno per ogni cifra. Le cifre decimali sono state disposte su una matrice 40*25 e l’assegnazione dei colori e’ stata fatta dando allo zero un colore freddo (blu) e passando gradualmente ai colori caldi fino al rosso della cifra 9. E’ proprio un bel effetto. Anche se, come per il caso in bianco e nero, non sembra emergere nessuna struttura particolare.

E’ possibile fare una cosa analoga usando due colori diversi per le cifre che sono numeri primi (2,3,5,7) e quelle non prime (0,1,4,6,8,9). Nel grafico sottostante i primi sono stati indicati in rosso. Come si può vedere neanche questa volta emerge una struttura particolare. Ma si possono fare delle osservazioni. Si notano, ad esempio, dei clusters di cifre prime circondate da un “mare” di cifre non prime, e alcuni clusters che rappresentano le lettere dell’alfabeto. Si può vedere chiaramente una T, una I, una L capovolta e cosi via. E’ possibile che si riescano a riprodurre tutte le lettere dell’alfabeto giocando con tutte le cifre decimali conosciute di pi greco? Chissà. Un’altra cosa che si può notare e’ che almeno per le prime 100 cifre decimali, e’ possibile trovare una traiettoria percolativa che ci permette di spostarci dalla parte superiore del reticolo a quella in basso (si ammettono movimenti in tutte e nove i primi vicini di ogni cella). E’ sempre vero questo se aggiungiamo altre cifre? In altre parole esiste, per esempio, una sequenza consecutiva di 40 cifre decimali che non siano cifre prime?

Visto che nelle rappresentazioni finora mostrate non emerge nessuna struttura particolare e’ lecito chiedersi se effettivamente questo sia ancora vero se si considerano tutte le cifre conosciute. In altre parole e’ possibile che pi greco sia un numero normale? In matematica “normale” significa che un numero in base 10, presenta nella sua espansione decimale tutte le cifre da 0 a 9 con frequenza media 1/10. Questo significa che la distribuzione delle cifre da 0 a 9 nell’espansione decimale di pi greco e’ completamente casuale. Ad oggi non si sa se pi greco e’ effettivamente normale, anche se le prime 30 milioni di cifre sono distribuite uniformemente. Come esempio qui di seguito viene riportata la frequenza delle cifre 0-9 per le prime cifre di pi greco. La variazione tra le cifre e’ veramente piccola e tutte tendono a 0.1. La stessa cosa e’ vera anche per l’espansione decimale del reciproco di pi greco.

 Frequenza delle cifre da 0 a 9 per le prime 1000000000000 cifre di pi greco.

Qualche curiosità prima di lasciarci. La sequenza di sei 9 consecutivi si trova alla 762ima cifra decimale di pi greco. Questa posizione nell’espansione di pi greco viene chiamata il punto di Feinman. La sequenza della posizione nell’espansione decimale di pi greco dove compaiono le prime n stringhe di 9 (con n=1,2,3,4...) e’ data da :

5, 44, 762, 762, 762, 762, 1722776, 36356642, 564665206

Questo significa che per trovare una stringa con nove 9 dobbiamo passare in rassegna la bellezza di 564665206 cifre decimali. Niente male. La sequenza 0123456789 compare più volte tra le cifre di pi greco. In particolare in posizione 17387594880, 26852899245, 30243957439, 34549153953, 41952536161, 43289964000. Stessa cosa per la sequenza 9876543210 che compare anche essa in diverse posizioni. E pensare che pi greco altro non e’ che il semplice rapporto della circonferenza e il raggio di un cerchio. Ancora la comparsa di complessità da operazioni (regole) molto semplici. Non e’ straordinario? Per finire una simpaticissima immagine ottenuta da Mike Keith usando le prime 768 cifre di pi greco disposte all’interno di un cerchio a cui tale costante e’ intimamente legata.