Blaise Pascal nacque a Clermont, in Francia, nel 1623 e morì a Parigi nel 1662. Egli fu un filosofo, matematico e scienziato e la sua vita e’ stata quella tipica del genio precoce. Fin dalla più giovane età fu introdotto allo studio della matematica e delle scienze dal padre Etienne, magistrato e appassionato cultore di scienze. A soli sedici anni scrisse un Saggio sulle sezioni coniche, in cui formulò uno dei teoremi fondamentali di geometria proiettiva, noto come “Teorema di Pascal”. A diciotto anni, nel 1641, egli costruì la prima macchina calcolatrice che fu poi ulteriormente migliorata otto anni dopo. Questa macchina, chiamata successivamente Pascalina, somiglia molto al primo calcolatore meccanico costruito nel 1940. Nel 1654, in collaborazione con il matematico Pierre de Fermat, elaborò la teoria delle probabilità, che e’ poi divenuta fondamentale in campi quali la statistica e la fisica. Tramite opportuni esperimenti confermò l’ipotesi di Evangelista Torricelli sugli effetti esercitati dalla pressione atmosferica sull’equilibrio dei liquidi. Tra i suoi contributi piu’ rilevanti vi sono la cosiddetta “legge di Pascal”, in base alla quale i fluidi esercitano la medesima pressione in tutte le direzioni, e le ricerche sul calcolo infinitesimale. Nel 1654 dopo alcuni anni di vita intensamente mondana, trasformò in una vocazione religiosa quello che fino ad allora era stato un atteggiamento solo benevolo nei confronti della fede. Elemento importante per il suo cambiamento fu l’ambiente giansenistico di Port-Royal dove sua sorella Jacqueline era monaca. Nel 1653 le tesi giansenistiche vennero messe al bando da Papa Innocenzo X; sebbene la posizione dell’ambiente di Port-Royal non coincidesse esattamente con quella di Giansenio anch’esso venne coinvolto nella condanna. In sua difesa Pascal scrisse le famose lettere conosciute come “Provinciali”, che divennero in poco tempo uno dei best-seller dell’epoca ed uno dei capolavori della letteratura francese. Tra i tanti lavori matematici il suo nome e’ legato anche a quello che oggi porta il suo nome: il Triangolo di Pascal (anche conosciuto come triangolo di Tartaglia). Egli ne analizzo’ le proprieta’ e le pubblico’ nel 1654 nel Traite’ du triangle arithmetique. Pascal comunque non fu il primo ad analizzare le proprietà’ di questo particolare triangolo; sembra infatti che questo sia stato scoperto indipendentemente dai Persiani e dai Cinesi nel secolo XI. Il matematico cinese Chia Hsien utilizzò questo triangolo per estrarre le radici quadrate e cubiche dei numeri. Dopo di lui altri autori cinesi si interessarono al triangolo tra cui Yang Hui che nel 1303 riportò una rappresentazione del triangolo come mostrato in fig. 1. Vediamo in cosa consiste questo triangolo e quali numeri ne entrano a far parte (oggi conosciuti come numeri di Pascal). Per prima cosa va detto che il triangolo di Pascal era diverso da quello che noi conosciamo oggi anche se le caratteristiche matematiche rimangono le stesse.

Figura. 1 Triangolo di Pascal in una rappresentazione cinese del secolo XIV.
Per costruire il suo triangolo, Pascal disegnò due linee perpendicolari, dopo di che divise ognuna di queste due linee in un numero di parti uguali tracciando degli assi verticali ed orizzontali in modo da creare delle celle. Una volta fatto ciò congiunse con una linea i due punti della prima divisione formando un triangolo di cui questa linea ne era la base. Dopo di che continuò con le altre celle formando così tanti triangoli quante erano le celle di un asse. Con una linea poi divise questi triangoli in due parti uguali. A questo punto cominciò ad inserire i numeri come segue. Il numero da inserire nella prima cella che forma l’angolo retto e’ arbitrario, ma una volta scelto, tutti gli altri numeri derivano da esso; per questa ragione esso e’ detto il generatore del triangolo. I numeri delle altre celle sono determinati dalla somma dei numeri nelle celle precedenti lungo lo stesso asse verticale ed orizzontale. Se ruotiamo l’asse di simmetria centrale di 45 gradi verso l’asse verticale otteniamo il triangolo così come lo conosciamo oggi (vedi figura 2 e 3). In questa forma (cioè quella della figura 3) i numeri di ogni cella vengono ottenuti dalla somma dei numeri delle due celle superiori adiacenti e supponendo che tutte le celle all’esterno del triangolo contengano zero. Adesso che abbiamo imparato a costruire il triangolo di Pascal vediamo quali sorprese si nascondono al suo interno.


Figura 3. Il triangolo di Pascal come viene rappresentato oggi
Una delle prime proprieta’ del triangolo e’ la sua simmetria. Infatti se prendiamo il triangolo e lo pieghiamo in corrispondenza dell’asse centrale (l’altezza del triangolo in figura 2) vedremo che i numeri si sovrappongono esattamente tra di loro. Andiamo avanti nell’individuare altre misteriose ed interessanti proprietà. Consideriamo la somma dei numeri presenti in ogni riga del triangolo.
1 = 1 = 20
1 + 1 = 2 = 21
1 + 2 + 1 = 4 = 22
1 + 3 + 3 + 1 = 8 = 23
1 + 4 + 6 + 4 + 1 = 16 = 24
………………
Come si vede la somma e’ uguale a 2 elevato al numero della riga presa in esame, assumendo che la prima riga sia la riga zero. Un’altra caratteristica interessante ha a che fare con i numeri primi. Possiamo osservare, infatti, che se il numero di una riga e’ un numero primo allora ogni numero contenuto in essa, eccetto i due numeri uno alle estremità, e’ divisibile per questo numero primo. Nella settima riga, per esempio, abbiamo i numeri 1, 7, 21, 35, 35, 21, 7, 1 con 7, 21 e 35 tutti divisibili per 7. Al contrario se il numero di una riga e’ composto, come la sesta riga (considerando sempre la prima riga come quella zero), questo non e’ vero. Per questa riga, infatti abbiamo i numeri 1, 6, 15, 20, 15, 6, 1 dove 15 e 20 non sono divisibili per 6. In termini matematici possiamo formulare il seguente teorema:
· Se n e’ un numero primo, allora i numeri centrali del triangolo di Pascal (cioè tutti i termini ad eccezione degli estremi) dell’ennesima riga sono divisibili per n.
Passiamo adesso ad esaminare i numeri lungo le diagonali del triangolo come mostrato in figura 4.

Figura 4. Le diagonali del triangolo di Pascal
La prima diagonale indicata con n, e’ la sequenza dei numeri interi. La seconda indicata con tn invece e’ la sequenza dei numeri triangolari, cioè la sequenza generata sommando tra loro il primo, il primo e il secondo, il primo e il secondo e il terzo numero naturale e cosi via. Cioè:
1
1+2=3
1+2+3=6
1+2+3+4=10
..........................
La terza diagonale e’ la sequenza dei cosiddetti numeri tetraedrici, cioè la somma dei numeri triangolari e cosi via. Quante scoperte affascinanti analizzando semplicemente le diagonali di questo triangolo. Adesso passiamo una cosa veramente sorprendente. Se si prende una diagonale che inizia in uno qualsiasi degli 1 sul bordo e terminante in un qualsiasi numero all’interno del triangolo, la loro somma e’ sempre uguale al numero al di sotto dei numeri selezionati e non sulla stessa diagonale (vedi figura 5).
1+6+21+56 = 84
1+7+28+84+210+462+924 = 1716
1+12 = 13

Figura 5. La mazza da Hockey
Tutte le strutture matematiche emerse fino ad ora tutto sommato erano abbastanza prevedibili. La prossima invece riguardante i numeri di Fibonacci non e’ immediata e bisogna guardare con attenzione per scoprirla. Tracciamo delle linee attraverso il triangolo come quelle mostrate in figura 6 e sommiamo i numeri che si trovano tra due linee adiacenti. I numeri così generati altro non sono che i numeri di Fibonacci. Ricordiamo brevemente che i numeri di Fibonacci iniziano con due 1 e tutti gli altri generati semplicemente sommando i due numeri precedenti (1, 1, 2, 3, 5, 8, 13, 21,.....).
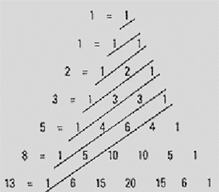
Figura 6. I numeri di Fibonacci
Proviamo a guardare, adesso, alla diagonale evidenziata nella figura 7. Sommiamo i primi due termini di questa diagonale: 1+3=4. Poi sommiamo il secondo col terzo: 3+6=9; il terzo con il quarto 6+10=16 e così via. Il triangolo di Pascal non finisce di meravigliarci. I numeri trovati altro non sono che la sequenza dei numeri quadrati.

Figura 7. I numeri quadrati all’interno di quelli triangolari.
Il triangolo di Pascal trova un’ampia applicazione anche in altre aree della matematica quale l’algebra e la statistica. Chiunque abbia qualche nozione di algebra ricordera’ che questa espressione:
(1+x)2
può essere sviluppata come:
(1+x)2=(1+x)(1+x)=1+2x+x2
e che la stessa cosa può essere fatta per un cubo:
(1+x)3=(1+x)(1+x)(1+x)=(1+x)(1+2x+x2)=1+3x+3x2+x3
Se guardiamo i coefficienti delle x ci accorgiamo che nel caso del quadrato questi sono i numeri della seconda riga (1,2,1) del triangolo di Pascal e che nel caso del cubo questi sono i numeri della terza riga (1,3,3,1). Si può provare per potenze maggiori di 3 e verificare di persona che i coefficienti di espansione sono proprio i numeri di Pascal. Generalizzando, l’n-sima riga del triangolo di Pascal da’ i coefficienti dello sviluppo di:
(x+y)n
Per esempio nel caso n=4 abbiamo:
(x+y)4=x4+4x3y+6x2y2+4xy3+y4
dove i coefficienti 1, 4, 6, 4, 1 sono i numeri della quarta riga del triangolo.
I numeri di Pascal possono essere usati anche nella teoria delle probabilità. Immaginiamo di avere cinque libri e che ne vogliamo prendere uno per leggerlo. In quanti modi diversi possiamo selezionare un singolo libro? Be’ questo e’ abbastanza facile. In cinque differenti modi. Se indichiamo con A, B, C, D, E i 5 libri possiamo scegliere una qualsiasi di queste cinque lettere e quindi abbiamo 5 possibilita’. Se vogliamo invece selezionare due libri? In questo caso possiamo avere le seguenti combinazioni:
AB, AC, AD, AE, BC, BD, BE, CD, CE, DE
cioè 10 possibili modi. E se vogliamo selezionare tre libri su cinque, quanti modi possibili abbiamo? Questo e’ la stessa cosa che scartare due libri da cinque e quindi ci sono 10 possibili modi. Selezionare invece quattro libri su cinque e’ la stessa cosa che scartare un libro su cinque e quindi in questo caso abbiamo cinque possibili modi. E uno solo per selezionare cinque libri su cinque. Chiaramente c’e’ un unico possibile modo per selezionare nessun libro su cinque. Riassumendo abbiamo:

Di nuovo i numeri di Pascal. Questo e’ uno degli aspetti affascinanti della matematica; due cose apparentemente non connesse tra loro che invece nella pratica lo sono. Le espansioni algebriche e la selezione degli oggetti. Il numero di modi di selezionare r oggetti da un totale di n si scrive come:
nCr
Così le selezioni precedenti possono essere scritte come segue:

In generale, quindi, per sapere quanti modi possibili ci sono per selezionare r oggetti su n basta prendere un triangolo di Pascal e tirar fuori i numeri dell’n-sima riga. Ma c’e’ un modo per calcolare nCr automaticamente senza dover prendere ogni volta il triangolo di Pascal? La risposta e’ si.
nCr=n!/((n-r)!r!)
n! e’ il cosiddetto fattoriale di n e significa moltiplicare tra loro tutti i numeri interi da 1 fino a n incluso. Per esempio 1!=1, 2!=1*2=2, 3!=1*2*3=6 e cosi via. Per definizione si assume che il fattoriale di zero e’ uguale a 1, cioè 0!=1. In definitiva i numeri di Pascal possono essere calcolati facilmente per qualsiasi numero n ed r che siano interi positivi utilizzando nCr A questo punto si potrebbe pensare che le meraviglie di questo oggetto semplice ma misterioso siano terminate. Ma non e’ cosi. Abbiamo solo graffiato la superficie di un iceberg. Vogliamo comunque adesso concentrarci sulla connessione tra il triangolo di Pascal e degli oggetti matematici entrati a far parte del nostro mondo dopo il lavoro del matematico Mandelbrot: i frattali. Facciamo una semplice operazione. Coloriamo di bianco i numeri pari del triangolo di Pascal e di rosso quelli dispari. All’apparenza veramente un’operazione banalissima eppure il risultato non e’ niente male.
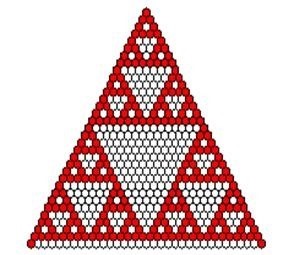
Figura 8. Le prime 32 righe del triangolo di Pascal. In rosso i numeri dispari e in bianco i pari.
Veramente straordinario. Una semplice operazione di divisione da’ vita ad un oggetto matematico con una profonda bellezza e simmetria. Possiamo anche complicarci un po’ la vita usando più colori. Come si fa? Semplicissimo. Decidiamo per quale numero vogliamo dividere i numeri di Pascal. Supponiamo 7. Una volta diviso un numero di Pascal per sette gli assegniamo un colore in base al resto della divisone. In questo caso possiamo avere sette diversi colori visto che il resto della divisone per 7 può dare: 0, 1, 2, 3, 4, 5 e 6. Il risultato di una tale operazione e’ mostrato in figura 9. A di là della pura bellezza estetica, questi triangoli nascondono delle proprietà interessanti? Come aspettato il triangolo di Pascal non poteva deluderci. La risposta ancora una volta e’ si. Essi, infatti sono dei frattali, cioè degli oggetti geometrici che presentano una struttura complessa e dettagliata ad ogni livello di ingrandimento e di cui gia’ abbiamo parlato ampiamente in questo blog. Tra le proprieta’ piu’ importanti c’e’ quella dell’invarianza di scala; in altre parole sono oggetti “auto somiglianti”, cioè ogni piccola porzione del frattale può essere vista come una riproduzione su scala ridotta dell’intera figura (vedi figura 10).
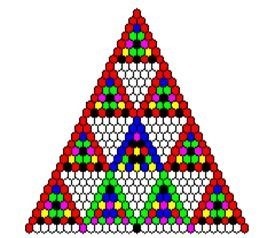
Figura 9. Le prime 32 righe del triangolo di Pascal. I colori sono assegnati in base al resto della divisione dei numeri del triangolo per 7.

 Figura 10. L’auto somiglianza del triangolo di Pascal
Figura 10. L’auto somiglianza del triangolo di Pascal
Osservando la figura 8 del triangolo di Pascal, si nota immediatamente la somiglianza con quello che oggi e’ conosciuto come triangolo di Sierpinski (porta il nome del suo scopritore). Per costruirlo si parte (vedi fig. 11) con un triangolo equilatero e si dividono i 3 lati a meta’ e da ognuno di questi punti si tracciano i lati di un nuovo triangolo equilatero che risultera’ essere ruotato rispetto a quello inziale. Il processo viene ripetuto all’infinito con l’unica accortezza di rimuovere in ognuno dei passi il nuovo triangolo al centro. Questo oggetto ha una dimensione di ~1.58 che sta ad indicare un oggetto geometrico che e’ tra una linea e una figura piana (di dimensione pari a 2) e con un area praticamente nulla. Strano vero? Certo. Ma e’ quello che succede con questi oggetti molto comuni in natura e scoperti meno di 100 anni fa.

Fig. 11 I primi passaggi per la creazione di un triangolo di Sierpinski. Indicando il triangolo inziale come ottenuto dall’iterazione zero, l’ultimo triangolo sulla destra avra’ ordine 4.
Nella fig. 12 un confronto da un triangolo di Sierpinski e il triangolo di Pascal della fig. 8. Osserviamo che il triangolo di Pascal ha dei piccoli vuoti bianchi isolati che possiamo trascurare cioe’ possiamo colorarli di rosso. Cosi facendo esso diventa simile al triangolo di Sierpinski di ordine 3.
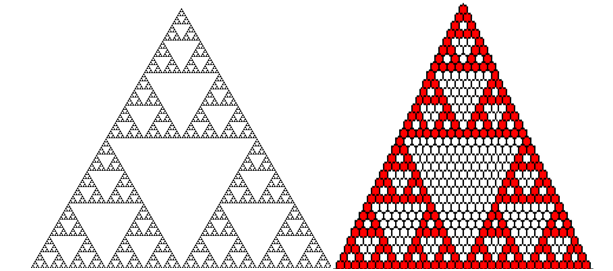
Fig. 12. Confronto da un triangolo di Sierpinski (sulla sinistra) e il triangolo di Pascal con in rosso i numeri dispari (sulla destra).
Fin qui la matematica e la grandiosita’ del genio di personaggi come Pascal, Sierpinski e Mandelbrot. E i Cosmati cosa c’entrano? Chi erano costoro? La mia attenzione si e’ focalizzata su questa famiglia del passato quando ho visitato i musei Vaticani. Tra le innumerevoli bellezze in essi presenti ci sono dei pavimenti nelle stanze del papa Sisto IV e della cappella Sistina da lui voluta che mi hanno lasciato stupito per la bellezza delle forme geometriche.

Fig. 13. La cappella Sistina
Il termine "Cosmati" è una generalizzazione dovuta al fatto che nelle iscrizioni epigrafiche che i costruttori romani lasciarono nelle loro opere, ricorreva spesso il nome di un certo "Cosma" (Cosmas, Cosmatus) di cui, dopo non poche difficoltà interpretative da parte degli studiosi tra la seconda metà del XIX e i primi decenni del XX secolo, si capi’ che tali nomi si riferivano a due artisti appartenenti a due famiglie parallele di marmorari, ma indipendenti: Cosma di Jacopo di Lorenzo (attestato tra il 1210 e il 1231) e Cosma di Pietro Mellini (1264-1279). Fu Camillo Boito, in un articolo dal titolo Architettura Cosmatesca, pubblicato nel 1860, ad "inventare" per la prima volta l'aggettivo "cosmatesca", da cui derivano gli altri sinonimi. La famiglia di marmorari romani più importante, che ebbe il privilegio di ricevere le più grandi committenze da parte del papato, fu quella di Tebaldo Marmorario (1100-1150), e soprattutto il figlio Lorenzo di Tebaldo e i successori Iacopo di Lorenzo, Cosma e i figli di quest'ultimo Luca e Iacopo alter. A rigore, quindi, si dovrebbe parlare di opere cosmatesche solo relativamente a quelle realizzate da questa famiglia. La loro fama e maestria nel campo dei mosaici sono state tali che oggi si parla di "stile cosmatesco" per indicare lo stile e le tecniche utilizzate da questi maestri e dai loro imitatori. Del capostipite Tebaldo Marmorario, vissuto a cavallo tra l'XI e il XII secolo, si hanno pochissimi riferimenti. Il figlio Lorenzo, detto appunto "di Tebaldo", è attestato in diversi lavori. Segue il figlio Iacopo "di Lorenzo" e il figlio di quest'ultimo Cosma "di Iacopo" o Cosma I; quest'ultimo, con i suoi due figli "carissimi" Luca e Iacopo II, o "alter" come spesso viene denominato dagli studiosi per distinguerlo dal nonno Iacopo I, sono gli ultimi della generazione della famiglia della bottega cosiddetta "di Lorenzo". I maggiori lavori cosmateschi conosciuti a Roma e nel Lazio, di cui molti firmati dagli stessi artisti, sono riferiti a Lorenzo, Iacopo, Cosma e i figli Luca e Iacopo II. Di seguito sono indicati i nomi di questi artisti:
Dell'altra famiglia, originata da Cosma di Pietro Mellini, si ricordano i figli di Cosma:
Questi geniali lavoratori del marmo divulgarono un nuovo tipo di decorazione che piacque molto, la diffusione delle loro opere lo dimostra, e quasi certamente quest’inedita elaborazione del mosaico, quest’originale sviluppo artistico che portò al nuovo gusto trova l’origine nel pavimento della chiesa abbaziale di Montecassino. Infatti il primo esempio conosciuto di stile cosmatesco, risale alla fine dell'XI secolo, tra il 1066 ed il 1071, quando l'abate Desiderio di Montecassino fece venire abili marmorari da Costantinopoli per rinnovare il pavimento della chiesa. All’inizio quindi prevalsero gli influssi di Bisanzio, dell’opus sectile e alexandrinum romana (vedi per es. Fig 14), ma poi si aggiunse anche il gusto arabo-siculo, che iniziava a farsi conoscere ed era chiaramente ispirato a motivi arabi (vedi esempio fig 15).


Fig. 14. Pavimenti di ville pompeiane ed ercolanesi. Sotto pavimento di una villa romana in Turchia.

Fig. 15. Riga sopra: motivi Cosmati di chiara ispirazione islamica. Sotto: alcune immagini del pavimento di Santa Sofia in Istanbul a cui sicuramente i Cosmati si ispirarono.
Il mosaico cosmatesco è formato da disegni geometrici preziosi, complessi, originali e differenti uno dall’altro. Si tratta di veri e propri coloratissimi tappeti marmorei la cui ricchezza e varietà contrasta con l’austera semplicità delle architetture romaniche nelle quali sono inseriti, nonostante l’inevitabile degrado prodotto dal trascorrere di quasi mille anni, riescono ancora a sopraffare i nostri sensi con la loro vibrante bellezza. Come in tutti gli artisti anche nei cosmati possiamo individuare degli elementi stilistici di base che si ripetono di volta in volta sui quali poi si sovrappongono elementi particolari a seconda delle esigenza specifiche che le diverse situazioni richiedevano. Gli elementi generali possono essere divisi in due strutture.
· Un elemento lineare chiamato guilloche (fig. 16 a sinistra), costituito da una serie di dischi o tondi che si connettono attraverso fasce che si intrecciano (immagine a sinistra sotto).
· Un elemento pentagonale chiamato il quinconce, una composizione di quattro tondi attorno a un quinto connesso agli altri ancora attraverso bande intrecciate (immagine a destra della fig 16).

Fig 16. La Guilloche (a sinsitra) e la Quinconce (a destra) dei cosmati
La maggior parte dello spazio del pavimento è suddivisa in una griglia di rettangoli, ognuno dei quali è riempito da un motivo geometrico sovrapponibile secondo due direzioni come una carta da parati. Questo tipo di motivi è denominato a carta da parati anche dai matematici (nel mondo anglosassone è molto diffusa la definizione wallpaper group per indicare il gruppo dei 17 motivi periodici del piano). Per simmetria intendiamo un movimento rigido del piano che porta a sovrapporre la figura a se stessa. Ad esempio ruotando il motivo rappresentato nella figura 17 di 180 gradi intorno al punto di contatto dei due quadrati bianchi piu’ grandi lo si porta a coincidere con se stesso.

Fig. 17. Motivo cosmato ottenuto con quadrati e loro diagonali.
A differenza dei motivi della navata centrale, i motivi geometrici (vedi fig 18) che riempiono i rettangoli che occupano, in parte o del tutto, la restante superficie pavimentata hanno un carattere a-direzionale, statico, fornendo così un ricco e coloratissimo tappeto marmoreo per gli spazi.

Fig. 18 Esempio di griglie rettangolari
Un aspetto singolare dello stile dei Cosmati e’ la varieta’ delle forme utilizzate nelle decorazioni: circolari, triangolari, rettangolari, quadrate, romboidali, esagonali, ottagonali e la vescica piscis (ovoidale ottenuta dall’intersezione di due cerchi). Spesso le forme sono ottenute le una dall’altra: un rombo ottenuto con due triangoli equilateri, un triangolo dividendo un quadrato lungo la diagonale, un rettangolo unendo insieme due quadrati e cosi via. Altre realizzazioni comportano combinazioni di queste forme dopo aver effettuato opportune rotazioni come per esempio un quadrato inscritto in un altro dopo una rotazione di 45 gradi, un triangolo inscritto in un altro dopo una rotazione di 180 gradi o anche piu’ circonferenze concentriche. La maggior parte delle decorazioni dei Cosmati segue una tecnica costruttiva molto ingegnosa: l’alternanza di forme piu’ grandi con altre piu’ piccole e composite che riempono gli spazi liberi. In altre parole, i Cosmati cominciavano il loro lavoro da una scala piu’ grande per finire a scale sempre piu’ piccole. La struttura piu’ semplice e’ quella di un quadrato con un altro all’interno ruotato di 45 gradi e inserendo poi nei triangoli ai vertici dei triangoli piu’ piccoli ruotati di 180 gradi (vedi fig. 19) oppure dividendo il quadrato con le due diagonali o utilizzando dei rettangoli al posto dei triangoli.

Fig. 19 Motivi Cosmati utilizzando quadrati e triangoli (ad quadratum e ad triangulatum)
Nonostante i mille anni che separano i Cosmati dagli artisti più recenti, alcune ricerche artistiche compiute dai Cosmati sono ancora oggi attuali. Nella loro ricerca sulla tassellatura del piano, il metodo costruttivo dei Cosmati implicava, come detto poco fa, la creazione di motivi di riempimento degli interstizi lasciati da una prima matrice determinata dalla posa dei tasselli più grandi. In alcuni casi era la forma dello stesso spazio da riempire a dettare le forme possibili di riempimento. Nell’esempio in fig. 20, l’inserimento di un triangolo equilatero nel tondo dettava il riempimento con altri triangoli simili, un processo che prevede dapprima la decomposizione di un modulo nei suoi sub-moduli congruenti e quindi la dilatazione della configurazione risultante fino a che i sub-moduli abbiano raggiunto le dimensioni dell’originale. Il procedimento satura il piano attraverso decomposizioni e dilatazioni iterate. Se il modulo di partenza è il triangolo equilatero, ne risulta un motivo che oggi riconosciamo come il triangolo di Sierpinski (fig. 20) o come tappeto di Sierpinski (fig. 21).
![image_thumb14[1] image_thumb14[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj7Sgnz2nGS7cUZa1jgAWJXWVOj3sXBIEOej-etXIQlqEe3K9-UQ6i22QG0u4a7cA0e4YLAeZcdImqhx5fuDjpEC1XwjfcOTivpQuvOkJmwN94UGVzFadd9Gsb-F6vYAsut_1QawbEW/?imgmax=800)
Fig. 20 Tre strutture auto-similari a forma triangolare oggi conosciute come triangoli di Sierpinski. I primi due sono d’ordine 3 mentre l’ultimo a destra e’ di ordine 4.

Fig. 21 Due cosiddetti tappeti di Sierpinski
L’abilita’ dei Cosmati puo’ essere ancora meglio apprezzata nei motivi con elementi curvilinei che richiedono delle approfondite conoscenze geometriche e sono molto difficili da realizzare. In questo caso i triangoli da Euclidei passano ad Iperbolici (vedi fig 22) e l’interno viene riempito con triangoli piu’ piccoli auto-similari come fatto per i triangoli piani (vedi fig 24 a destra).

Fig. 22 Triangolo iperbolico
I triangoli iperbolici hanno la somma degli angoli interni minore di 180 gradi mentre quelli sferici hanno la somma maggiore di 180 come mostrato in fig. 23. I triangoli curvilinei dei Cosmati somigliano molto al frattale di Apollonio riportato in figura 24 a sinistra.
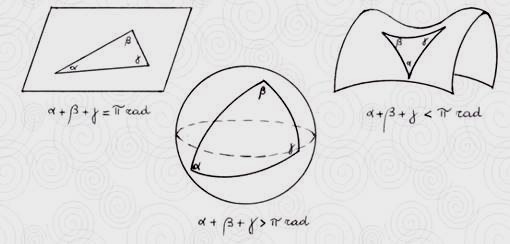
Fig. 23 Le tre geometrie: euclidea, sferica ed iperbolica

Fig. 24 Il frattale di Apollonio a sinistra. Inserimento di cerchi auto-similari all’interno di un triangolo
iperbolico. A destra un triangolo di Sierpinski curvilineo.
Nelle figure seguenti alcuni esempi di pavimenti Cosmati con triangoli di Sierpinski curvilinei (vedi fig. 25 e 26) mentre nella figura 27 altri esempi di triangoli di Sierpinski nel piano (fig 27).

Fig. 25 Due esempi di rote con dentro triangoli di Sierpinski curvilinei

Fig. 26 Altri esempi di triangoli di Sierpinski curvilinei.


Fig. 27 Altri esempi di pavimenti Cosmatiani con triangoli di Sierpinski piani
Come e’ possibile che i Cosmati possano essere giunti a quello che noi oggi chiamiamo il triangolo di Sierpinski senza avere a disposizione le nostre conoscenze matematiche e geometriche? I frattali come gia’ anticipato sono una branca della geometria sviluppata negli ultimi cinquant’anni o forse meno. E’ vero come riportato da molti studiosi che i Cosmati molto probabilmente sono giunti a questi oggetti senza sapere cosa fossero grazie solo alla loro tecnica di riempimento dello spazio partendo da oggetti piu’ grandi e pian piano arrivando a riempire gli spazi piu’ piccoli con oggetti di dimensioni ridotte? E’ possibile. Ma ci potrebbe essere anche un’ ipotesi alternativa altrettanto valida. Basterebbe non pensare al triangolo di Sierpinski ma semplicemente al triangolo di Pascal e al suo motivo ottenuto colorando i numeri pari e quelli dispari come quello della fig 12. Perche’ i Cosmati con quella che si ritiene essere stata la loro tecnica non arrivarono ad un motivo simile al frattale di Apollonio della fig. 28? Dopo tutto si trattava di partire sempre con un triangolo curvilineo, inserire al centro un cerchio grande e poi via via cerchi sempre piu’ piccoli come fatto per i triangoli. Ma di questa figura non c’e’ traccia nei loro pavimenti.

Fig 28. Pseudo frattale di Apollonio ottenuro a partire da un triangolo iperbolico
e riempito con dei cerchi di diverse dimensioni
Di sicuro sappiamo che il triangolo di Pascal era noto ai persiani intorno all’anno mille e che di sicuro i Cosmati si sono rifatti all’arte islamica come quella della basilica di Santa Sofia di Istanbul o della Cappella Palatina di Palermo. L'Impero islamico arrivò a dominare, nell'VIII secolo d.C. il Nord Africa, la Penisola iberica e parte dell'India. Entrarono così in contatto con la matematica ellenistica e con quella indiana. Nella seconda metà del VIII secolo Baghdad divenne un nuovo centro del sapere a livello mondiale. Sovrani come al-Mansur, Harun al-Rashid e al-Ma'mun si dimostrarono attenti nei confronti della matematica e preservarono dalla distruzione molte opere matematiche greche che altrimenti sarebbero probabilmente andate perse. Thābit ibn Qurra fondò una scuola di traduttori che tradusse in arabo le opere di Archimede, Euclide e Apollonio. Gli Arabi tradussero, inoltre, molti testi indiani. Questi fatti contribuirono non poco alla nascita della matematica islamica. Molti tra i più grandi matematici islamici erano persiani. Muhammad ibn Musa al-Khwarizmi (780-850 Ca), un matematico persiano, scrisse importanti volumi sul sistema di numerazione indiano e sui metodi per risolvere equazioni. La parola "algoritmo" deriva dal suo nome e "Algebra" dal titolo della sua opera più importante, l'al-Jabr wa al-muqābala. In questa opera Al-Khwarizmi oltre a introdurre il sistema decimale nel mondo arabo trova metodi grafici e analitici per la risoluzione delle equazioni di secondo grado con soluzioni positive. Il nome al-jabr si riferisce al nome che il matematico dà all'operazione di riduzione di termini uguali da parti opposte dell'uguale tramite sottrazione. Per questi motivi egli è considerato da molti il fondatore dell'algebra moderna. Altri sviluppi alla materia furono apportati da Abu Bakr al-Karaji (953-1029) nel suo trattato al-Fakhri. Nel X secolo, Abu l-Wafa tradusse le opere di Diofanto in arabo e studiò la trigonometria ottenendo le formule di addizione e sottrazione per il seno. Alhazen studiò invece l'ottica. Omar Khayyam (1048-1131) fu poeta e matematico. Scrisse le Discussioni sulle difficoltà in Euclide nel quale tentava di dimostrare il quinto postulato di Euclide riguardante le rette parallele (data una retta e un punto fuori di essa esiste solo una parallela alla retta data passante per quel punto) partendo dagli altri quattro; impresa che sarebbe poi diventata un "chiodo fisso" per i matematici. Diede una soluzione geometrica all'equazione di terzo grado ma non riuscì a risolverla per radicali. Egli nella sua opera Algebra descrive una regola da lui trovata per determinare le potenze successive di un binomio e quindi arriva a quello che oggi conosciamo come triangolo di Pascal. Il periodo di Omar e’ lo stesso del capostipite della famiglia dei Cosmati, Lorenzo Marmorario vissuto nella seconda meta’ del 1100. E’ possibile che la conoscenza del triangolo di Pascal possa essere passata dalla Persia all’Italia attraverso la cultura islamica? Amato da Montecassino nella sua Historia Normannorum, chiama in causa la possibile presenza di artefici “saraceni” giunti a Montecassino da Alessandria. La presenza certa di artigiani musulmani attivi in Italia meridionale è documentata dalla particolare decorazione in opus sectile e opus tessellatum dell’abside della chiesa di San Nicola a Bari, eseguita presumibilmente durante il priorato dell’abate benedettino Eustasio, tra il 1105 ed il 1123, se non qualche anno prima come riportato da Ruggero Longo nel suo lavoro di Tesi. Il motivo ornamentale che delimita l’emiciclo absidale del San Nicola mostra il monogramma di Allah in caratteri cufici reiterato più volte. La circolazione di musulmani nel meridione è assicurata d’altra parte dal fiorente centro di Amalfi che faceva da anello di congiunzione tra la costa campana, gli empori islamici nordafricani e il medi-oriente musulmano e bizantino. Gli amalfitani trovarono terreno fertile a Salerno quando, a partire dall’inizio del secolo XII, la città raggiunse un notevole sviluppo economico, divenendo un centro fiorente. È plausibile che le maestranze benedettine giunte nella fascia costiera della Campania abbiano accolto elementi della cultura islamica, rinnovando il linguaggio artistico di matrice bizantina attraverso la partecipazione diretta di artefici di origine musulmana, depositari di un linguaggio decorativo estraneo alla tradizione occidentale. Un primo incontro tra la cultura bizantino cassinese e quella islamica potrebbe essere avvenuto proprio a Salerno. Gli intensi rapporti tra Palermo e Salerno potrebbero aver garantito l’insediamento e la collaborazione di artigiani siciliani nel cantiere campano. Non è da escludere inoltre che si sia verificato anche il caso contrario. Anzi è probabile che Ruggero II, ammirando l’impianto del Duomo, abbia disposto l’esecuzione del pavimento palatino assumendo artigiani salernitani. L’ ipotesi trova conferma immediata nelle rilevanti analogie tra i micromodelli adoperati nei monumenti delle due città (Fig. 29 e 30). Da quanto esposto emerge che almeno due squadre di marmorari erano attive nei territori normanni. Una in Campania e un’altra in Sicilia e di sicuro in contatto tra loro. Attraverso la Sicilia le maestranze peninsulari recuperarono le relazioni con la cultura bizantina e con quella islamica. Dalla mescolanza di queste culture e’ possibile che in Italia sia arrivato quello che noi oggi conosciamo come triangolo di Pascal e che il motivo ottenuto colorando semplicemente i numeri pari e dispari abbia colpito cosi tanto i Cosmati da convincerli ad utilizzarlo un po’ ovunque nelle loro bellissime opere. E’ un ipotesi che difficilmente potra’ essere provata. Ma molto piu’ facile da accettare di quella della scoperta occasionale da parte di alcuni marmorari medievali del concetto di frattale e quindi del triangolo di Sierpinki. Ai posteri l’ardua sentenza.
 Fig. 29 A sinistra, motivi ornamentali in opus sectile del Duomo di Salerno. A destra, Cappella Palatina di palermo
Fig. 29 A sinistra, motivi ornamentali in opus sectile del Duomo di Salerno. A destra, Cappella Palatina di palermo

Fig. 30. A sinistra: Duomo di Salerno, micromodello a nastri intrecciati del pluteo di recinzione in opus sectile. A destra: Cappella Palatina di Palermo, micromodelli a nastri intrecciati delle decorazioni in opus sectile delle pareti.
 Il gioco giapponese del sudoku, affonda le sue radici nei quadrati magici studiati da Eulero.
Il gioco giapponese del sudoku, affonda le sue radici nei quadrati magici studiati da Eulero.  Figura 2: Tecnica della singola posizione.
Figura 2: Tecnica della singola posizione.  Figura 3: Tecnica del singolo candidato (da sinistra verso destra).
Figura 3: Tecnica del singolo candidato (da sinistra verso destra).  Figura 4: Tecnica della singola linea (da sinistra verso destra).
Figura 4: Tecnica della singola linea (da sinistra verso destra).  Figura 5: Tecnica della catena forzata (da sinistra verso destra).
Figura 5: Tecnica della catena forzata (da sinistra verso destra).  Figura 6: Tecnica della catena forzata (da sinistra verso destra).
Figura 6: Tecnica della catena forzata (da sinistra verso destra).  Figura 8: Griglia del Sudoku etichettata con le lettere.
Figura 8: Griglia del Sudoku etichettata con le lettere.  Figura 9: Griglia di Sudoku che rimane la stessa in seguito ad operazione di rotazione e ri-etichettatura
Figura 9: Griglia di Sudoku che rimane la stessa in seguito ad operazione di rotazione e ri-etichettatura  Figura 10: Metodo del ciclo non ripetitivo di Eppstein.
Figura 10: Metodo del ciclo non ripetitivo di Eppstein. 





![image_thumb[25] image_thumb[25]](https://lh3.googleusercontent.com/-IhyqDnVo_Us/WBT8pKmfXsI/AAAAAAAAGl0/VRQgHeknI2Y/image_thumb%25255B25%25255D_thumb.png?imgmax=800)
![image_thumb[26] image_thumb[26]](https://lh3.googleusercontent.com/-6ttIWXKzE2o/WBT8qVhWCLI/AAAAAAAAGl8/kRa_g7WpURg/image_thumb%25255B26%25255D_thumb.png?imgmax=800)
![image_thumb[27] image_thumb[27]](https://lh3.googleusercontent.com/-84fxFCInx-4/WBT8rsbl_II/AAAAAAAAGmE/Z2N6h1HeB54/image_thumb%25255B27%25255D_thumb.png?imgmax=800)
![image_thumb[29] image_thumb[29]](https://lh3.googleusercontent.com/-T6lJkFdsbZk/WBT8tFVaiUI/AAAAAAAAGmM/1dfTtZn-BnI/image_thumb%25255B29%25255D_thumb.png?imgmax=800)
![image_thumb[6] image_thumb[6]](https://lh3.googleusercontent.com/-a3Q6J5X752s/WBT8uWok6lI/AAAAAAAAGmU/R7aoNlsXyIk/image_thumb%25255B6%25255D_thumb.png?imgmax=800)
![image_thumb[7] image_thumb[7]](https://lh3.googleusercontent.com/-kSwrKHpQJCE/WBT8vvn_9vI/AAAAAAAAGmc/O4G4Mb4yUjo/image_thumb%25255B7%25255D_thumb.png?imgmax=800)
![image_thumb[32] image_thumb[32]](https://lh3.googleusercontent.com/-CwZVzglNxJY/WBT8w0uxqAI/AAAAAAAAGmk/lJXxWmN96Nc/image_thumb%25255B32%25255D_thumb.png?imgmax=800)
![image_thumb[23] image_thumb[23]](https://lh3.googleusercontent.com/-mJ2V0DQ6a6I/WBT8ye9ghcI/AAAAAAAAGms/wR187UjYIu4/image_thumb%25255B23%25255D_thumb.png?imgmax=800)
![image_thumb[18] image_thumb[18]](https://lh3.googleusercontent.com/-es8ThldvL0U/WBT80m-Wj5I/AAAAAAAAGm0/JhCgVi_eDGU/image_thumb%25255B18%25255D_thumb.png?imgmax=800)
![image_thumb[11] image_thumb[11]](https://lh3.googleusercontent.com/-oT6U65nGtG4/WBT814gnnzI/AAAAAAAAGm8/yBaH4F8TVJ0/image_thumb%25255B11%25255D_thumb.png?imgmax=800)
![image_thumb[12] image_thumb[12]](https://lh3.googleusercontent.com/-gZAzXp0SoYs/WBT83J1320I/AAAAAAAAGnE/YseaFmrP418/image_thumb%25255B12%25255D_thumb.png?imgmax=800)
![image_thumb[13] image_thumb[13]](https://lh3.googleusercontent.com/-gjFauWyDA5s/WBT84CXaN7I/AAAAAAAAGnM/Jr_3KfEYBrQ/image_thumb%25255B13%25255D_thumb.png?imgmax=800)
![image_thumb[14] image_thumb[14]](https://lh3.googleusercontent.com/-fcZHf8sZyjA/WBT85lXRPKI/AAAAAAAAGnU/vFng5GGf2EE/image_thumb%25255B14%25255D_thumb.png?imgmax=800)























![image_thumb14[1] image_thumb14[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj7Sgnz2nGS7cUZa1jgAWJXWVOj3sXBIEOej-etXIQlqEe3K9-UQ6i22QG0u4a7cA0e4YLAeZcdImqhx5fuDjpEC1XwjfcOTivpQuvOkJmwN94UGVzFadd9Gsb-F6vYAsut_1QawbEW/?imgmax=800)











