Gli adroni come bisturi di precisione

 

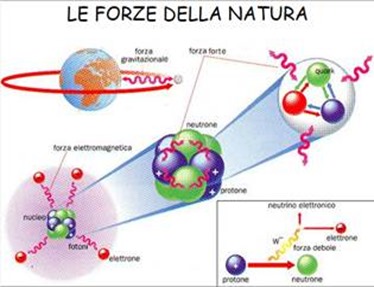
E’ di solo pochi giorni fa la notizia di una bimba di 9 anni affetta da un tumore raro (cordoma) che interessa i due estremi della colonna vertebrale curata con i protoni. La terapia che è stata messa in atto si basa sull’utilizzo di fasci di protoni e ioni pesanti. Si tratta di una tecnica all’avanguardia per il trattamento dei tumori più precisa e che provoca meno danni ai pazienti. Nel mondo non sono molti i centri che utilizzano questo tipo di cura: a livello mondiale sono soltanto 48. Vediamo di capire allora come funziona questa nuova e promettente tecnica di bombardamento. Non e’ la prima volta e non sara’ nemmeno l’ultima che la ricerca fondamentale ha ricadute molto importanti nel campo della medicina. Le proprieta’ quantistiche della materia, le radiazioni, l’antimateria, gli acceleratori di particelle e i rivelatori, sono usciti dai laboratori dei fisici per entrare nel mondo degli ospedali per aiutare i medici a guardare dentro i nostri corpi e curare diverse patologie tra cui il cancro. Questo termine indica un processo patologico caratterizzato dall’abnorme accrescimento di un tessuto che determina la comparsa di una tumefazione localizzata con disturbi legati a distruzione del tessuto normale preesistente, a compressione di strutture vicine o a ostruzioni di visceri cavi con ristagno dei secreti in essi contenuti.

In tutti i tumori si riconoscono due componenti di base:

1. il parenchima costituito dalle cellule neoplastiche o trasformate, ovvero quelle cellule che hanno subito un’alterazione genica che causa la crescita anormale del tessuto.

2. lo stroma che funge da sostegno per la massa tumorale ed `e composto da tessutto connettivo e vasi sanguigni.

Sebbene siano le cellule parenchimali a costituire la parte proliferativa della neoplasia, la crescita e l’evoluzione tumorale sono strettamente connesse e influenzate dallo stroma: e’ quest’ultimo infatti che fornisce la struttura di sostegno su cui proliferano le cellule trasformate.

L’evoluzione della maggior parte dei tumori maligni puo’ essere divisa in quattro fasi:

· modificazione maligna delle cellule bersaglio, denominata trasformazione;

· crescita delle cellule trasformate;

· invasione locale

· e, infine, metastasi a distanza (cioe’ localizzazione secondarie a distanza).

La crescita della massa tumorale e la sua velocita’ e’ determinata dalla differenza tra il numero di cellule alterate prodotte e le cellule perse (apoptosi – eliminazione di cellule alterate tramite meccanismo di morte programmata come avviene per esempio nell’embrione umano durante la differenziazione delle dita delle mani e dei piedi generando la morte delle cellule che costituiscono le membrane interdigitali di mani e piedi palmati). In genere, lo squilibrio tra cellule prodotte e cellule perse e’ piu’ alto nei tumori con una frazione di crescita alta. Alcuni linfomi, leucemie e carcinomi polmonari sono caratterizzati da frazioni di crescita elevate e si manifesta un decorso clinico estremamente rapido: il tumore si dice aggressivo. Tumori piu’ largamente diffusi, come il tumore alla mammella e al colon hanno una bassa frazione di crescita e la produzione cellulare supera la perdita di appena il 10 per cento. Il ritmo di accrescimento e’ dunque molto piu’ lento. La frazione di crescita delle cellule tumorali ha un notevole impatto sulla loro suscettibilita’ alla chemioterapia (trattamento terapeutico a base di sostanze chimiche). La maggior parte dei farmaci contro il cancro, infatti, agisce sulle cellule che si trovano nel ciclo replicativo; percio’ i tumori che hanno una frazione di crescita bassa, ad esempio solo del 5 per cento, avranno una crescita lenta, ma saranno refrattari ai trattamenti chemioterapici classici. In questi casi, si ricorre ad altre tecniche di riduzione della massa tumorale di tipo non farmacologico, ad esempio la radioterapia (di cui parleremo a breve) o l’intervento chirurgico. Lo scopo e’ ridurre il numero di cellule tumorali che si trovano nella fase G₀ (cellule in una fase di quiescenza temporanea o irreversibile, o in altri termini che hanno interrotto la fase di replicazione) del ciclo cellulare, in modo che le cellule tumorali residue tendano ad entrare nel ciclo replicativo e pertanto diventino sensibili all’azione dei farmaci. Al contrario, tumori aggressivi (come certi linfomi) che contengono un gran numero di cellule nel ciclo replicativo si dissolvono con la chemioterapia e possono anche essere guariti.

Nella crescita di un tumore, inoltre, si distinguono due fasi: una prima fase di evoluzione avascolare e una seconda fase caratterizzata dalla capillarizzazione della massa tumorale. I tumori, infatti, stimolano la crescita dei vasi ematici dell’ospite, processo detto angiogenesi, che e’ essenziale per rifornire di sostanze nutritive le cellule tumorali. Fintanto che la massa tumorale e’ poco estesa (un diametro o uno spessore inferiore ai 2mm), le cellule tumorali riescono a ricevere l’apporto di nutrienti e ossigeno necessari alla loro vita per diffusione dai capillari gia’ esistenti, ma per superare tale soglia e’ necessario un processo di vascolarizzazione. Durante la crescita del tumore, alcune cellule acquisiscono un fenotipo angiogenetico, che gli permette di produrre segnali che inducono la proliferazione delle cellule endoteliali (quelle che rivestono l’interno dei vasi sanguigni e di quelli linfatici), che vanno a costituire i nuovi vasi ematici. Il cambiamento da tumore avascolare a tumore vascolare e’ detto switch angiogenetico. Contrariamente ai vasi normali, i vasi di origine tumorale possono crescere in continuazione, sotto l’azione di fattori di crescita specifici come il VEGF (la proteina piu’ importante di questa categoria e’ il VEFG-A), e costituiscono un sistema ematico irregolare e dalla forma tortuosa. Questo fa si che non tutte le cellule del tumore ricevano il nutrimento necessario, e quindi si creano delle necrosi all’interno della massa tumorale stessa. La vascolarizzazione del tumore e’ una delle condizioni che favorisce maggiormente l’invasivita’ e la metastatizzazione dei tumori maligni. Proprio perche’ l’angiogenesi e’ determinante per la crescita e la diffusione dei tumori, nelle terapie e’ rivolta una grande attenzione ai farmaci che inibiscono questo processo. Rientrano in questa categoria i nuovi farmaci biologici monoclonali come l’avastin (bevacizumab) la cui azione e’ schematizzata nelle immagini sottostanti. In parole semplici l’azione di questi farmaci e’ quella di bloccare i VEGF prodotti dalle cellule tumorali e responsabili della crescita anomala dei vasi sanguigni.

Per quanto riguarda la velocita’ di crescita questa e’ correlata al livello di differenziazione cellulare: meno e’ alto il livello di differenziazione piu’ `e veloce la crescita. Quindi la maggior parte dei tumori maligni cresce piu’ rapidamente rispetto i tumori benigni. Inoltre, la velocita’ di crescita e’ spesso non costante nel tempo perche’ fattori come la stimolazione ormonale, l’adeguatezza dell’apporto ematico e altri fattori ad oggi ancora poco conosciuti possono condizionare la cinetica cellulare. Questo rende la crescita e dimensione di un tumore praticamente impredicibile.

La terza fase, quella dell’invasione locale, avviene in modo differente per tumori benigni e maligni. Quasi tutte le neoplasie benigne crescono formando masse compatte ed espansive che restano localizzate nella loro sede di origine e non hanno la capacita’ di infiltrare gli organi circostanti o invadere a distanza. Poiche’ la loro espansione e’ piuttosto lenta, sviluppano al loro intorno un tessuto connettivo fortemente compresso, detto capsula fibrosa, che li separa dal tessuto d’origine. La crescita dei tumori maligni, invece, e’ accompagnata da una progressiva infiltrazione, invasione e distruzione dei tessuti circostanti. Solitamente le neoplasie maligne sono poco demarcate dal tessuto normale circostante e hanno una crescita irregolare e disomogenea. I tumori maligni a lenta espansione possono sviluppare una capsula fibrosa, ma, generalmente, sviluppano anche delle filiere di cellule che infiltrano le strutture adiacenti.

Queste filiere sembrano al microscopio delle chele di granchio e per questo il tumore maligno e’ anche detto cancro. Nella loro espansione i tumori maligni non rispettano, in genere, i normali confini anatomici e questo rende difficile l’intervento chirurgico di asportazione e, anche qualora il tumore apparisse compatto e ben circoscritto, e’ sempre necessario asportare anche una parte di tessuto sano limitrofo. L’invasivita’ dei tessuti circostanti e’ una delle principali caratteristiche del decorso clinico che permette di distinguere un tumore maligno da uno benigno.

La quarta fase, quella delle metastasi, e’ caratteristica solo delle neoplasie maligne. Le metastasi sono impianti di tumore lontani dal tumore primitivo. L’invasivita’ che caratterizza i tumori maligni permette loro di penetrare nei vasi ematici e linfatici nonche’ nelle cavita’ del corpo. Quelle appena indicate sono le tre principali vie di diffusione per i tumori maligni, che danno l’opportunita’ al cancro di diffondere in altre sedi. Solitamente, tanto piu’ il tumore primitivo e’ aggressivo e di rapido accrescimento, maggiore e’ la possibilita’ che metastatizzi o abbia gia’ metastatizzato.

Piu’ si studiano i tumori e piu’ si capisce quanto essi siano purtroppo intelligenti. Non c’e’ dubbio che come tutte le cellule anche quelle tumorali soddisfano il principio di evoluzione di Darwin e quindi escogitano nuove strategie pur di sopravvivere. Tra queste ricordiamo quelle messe a punto dal tumore del pancreas per ingannare il sistema immunitario o quelle del glioblastoma (tumore del cervello) che e’ in grado di trasformare alcune delle proprie cellule in vasi sanguigni per potersi cosi autoalimentare. Per questo motivo laddove la chirurgia e la chemioterapia non sono d’aiuto e’ possible utilizzare tecniche alternative date in prestito alla medicina dalla fisica nucleare e particellare. L’idea di base e’ di utilizzare le radiazioni per danneggiare il DNA delle cellule tumorali e determinarne cosi la morte.

Tra queste tecniche ricordiamo la radioterapia (generalmente raggi X), i fotoni di alta energia (raggi gamma), generati da sorgenti radioattive, quali il cobalto-60, oppure i fasci di elettroni. Questa radiazione viene indirizzata sull’organismo in corrispondenza del tessuto tumorale e, una volta dentro il corpo, viene assorbita durante il suo percorso da tutti i tessuti e gli organi, non soltanto laddove c’è un tumore, generando i ben noti effetti secondari. Questo, tra l’altro, limita la quantità di radiazione che si può utilizzare, in quanto un utilizzo massiccio mette a rischio la vita stessa del paziente. Una nuova tecnica a disposizione degli oncologi per combattere il cancro e’ quella dell’adroterapia in cui le cellule malate vengono sparate con un acceleratore di particelle.

Fasci di protoni oppure di ioni di carbonio, provenienti da acceleratori dedicati, sono utilizzati con grande successo per il trattamento dei tumori localizzati. L’idea di utilizzare i protoni per il trattamento dei tumori fu proposta nel 1946 da R.R. Wilson ed è stata applicata per la prima volta nel 1954 nel laboratorio di ricerca di fisica nucleare del Lawrence Berkeley National Laboratory, in California, Stati Uniti. In Europa il metodo è stato utilizzato in Svezia, a Uppsala, per la prima volta nel 1957, utilizzando un acceleratore che era stato costruito per ricerche di fisica fondamentale. Da allora, la tecnica si è molto perfezionata ed estesa in tanti paesi del mondo, inclusa l’Italia. Il nome della terapia deriva dal fatto che le particelle che vengono utilizzate, protoni oppure ioni di carbonio, sono adroni – particelle cioe’ composte da quark e che subiscono interazioni forti.

I protoni e gli ioni di carbonio utilizzati nell’adroterapia grazie a delle macchine chiamate acceleratori vengono portati ad una certa energia, che dipende dalla tipologia e localizzazione del tumore, e indirizzati con precisione elevatissima sul paziente.

Entrati nell’organismo, a differenza dei fasci di fotoni o di elettroni, viaggiano sino ai tessuti tumorali danneggiando pochissimo gli altri tessuti, rilasciando invece un’enorme quantità di energia, nel tessuto tumorale. I tessuti sani subiscono pochi danni, mentre quelli malati sono distrutti. Come si puo’ notare dal grafico sottostante la dose massima di energia rilasciata dai protoni e’ piu’ in profondita’ rispetto a quella dei raggi X. Il picco di rilascio dell’energia da parte dei protoni e’ chiamato picco di Bragg.

Controllando l’energia dei fasci si può controllare il posto dove questi rilasciano la loro carica distruttiva nell’organismo. Per tumori superficiali l’energia è più piccola che per un tumore profondo. La terapia con ioni di carbonio ha il vantaggio di avere una maggiore densità di ionizzazione rispetto a quella dei protoni. In questo modo i danni della struttura del DNA all’interno della cellula tumorale si verificano più frequentemente e così diventa più difficile per la cellula cancerosa riparare il danno. L’efficienza biologica della dose è più grande rispetto a quella dei protoni di un fattore tra 1,5 e 3. L’utilizzo degli ioni di carbonio ha però uno svantaggio: la dose, superato il posto dove è localizzato il tumore, non diminuisce a zero, come nel caso dei protoni, in quanto le reazioni nucleari stesse tra gli ioni di carbonio e gli atomi del tessuto portano alla produzione di ioni più leggeri, che possono creare piccoli danni nelle vicinanze del tessuto tumorale (alcuni progetti di ricerca stanno studiando proprio questo aspetto).

Per eseguire l’adroterapia sono necessari:

• un acceleratore di protoni e/o di ioni, che produce più fasci di particelle in modo tale da avere più sale di trattamento;

• un sistema di trasporto dei fasci nelle sale di trattamento;

• un sistema molto preciso di posizionamento del paziente;

• un sistema accuratissimo di controllo dell’energia dei fasci e della dose assorbita dal paziente;

• un sistema tridimensionale di trattamento personalizzato sul paziente ottenuto integrando le immagini diagnostiche ottenute applicando tecniche quali la tomografia a emissione di positroni o la tomografia computerizzata.

Il protocollo di trattamento dipende ovviamente dalla tipologia del tumore. Vengono trattati i tumori localizzati, per esempio i melanomi dell’uvea, occhio, i tumori della base del cranio e della colonna vertebrale e anche alcuni tumori solidi pediatrici. Dopo l’iniziale calibrazione dell’energia, vengono effettuate un numero variabile, 12-16 d’abitudine, di sedute di trattamento.

Alla fine del 2012 esistevano nel mondo circa 40 centri di adroterapia e quasi 100.000 pazienti trattati con fasci adronici. Recentemente è entrato in funzione anche il centro italiano CNAO, vicino a Pavia, per l’adroterapia. L’adroterapia è un metodo molto costoso: l’investimento iniziale è intorno ai 100 milioni di Euro, e i costi per singolo paziente sono a loro volta molto alti – arrivando a decine di migliaia di Euro, un fattore almeno due volte più grande del costo della radioterapia. Oggi i ricercatori di tutto il mondo stanno provando nuovi metodi per costruire acceleratori meno costosi e riuscire a trattare più pazienti con questo metodo molto efficace per i tumori localizzati.

Quando la topologia incontra i big data

 

I big data stanno ricevendo sempre piu’ attenzione da parte dei media,  industrie, laboratori, banche e governi per citarne alcuni. La quantita’ di dati generata ogni giorno, (dalle condizioni meteorologiche ai telefonini, dal web ai satelliti….. ) e’ enorme e molti dei database contengono centinaia e centinaia di variabili (attributi). Si tratta di insiemi cosi grandi e complessi che i metodi tradizionali di analisi  spesso falliscono. Ma allora perche’ cosi tanto interesse? Perche’ i dati contengono informazioni estremamente importanti ed interessanti. Sono delle vere e proprie’ miniere da cui estrarre l’oro (cioe’ l’informazione). Ma questa estrazione non e’ semplice e cio’ non solo a causa del numero di variabili e del numero di istanze ma anche a causa della rumorosita’ e complessita’ dei database. Facciamo un esempio ricorrendo al concetto di correlazione lineare, il cui obiettivo e’ quello di trovare la migliore retta che approssimi un insieme di punti in un piano. Qui di seguito un esempio di correlazione tra l’altezza e peso di un gruppo di persone. L’equazione della retta e’ data da Altezza(Height)=0.6*Peso(Weight)+130.2 il che significa che per esempio una persona che pesa 100 Kg sara’ alta circa 190 cm.

Di sicuro una linea retta e’ una forma e questa e’ adatta a rappresentare i punti del grafico. Questo pezzo di informazione e’ molto importante per diverse ragioni. Una e’ che la forma ci da’ un’informazione qualitativa mostrandoci come la variabile altezza varia direttamente con la variabile peso (cioe’ l’altezza aumenta se aumenta il peso). Un’altra e’ che essa permette di prevedere con ragionevole accuratezza una delle due variabili se conosciamo il valore dell’altra. La forma e’ alla base di una nuova metodologia che applica la topologia all’analidsi dei dati (Topology Data Analysis). Per il nostro esempio e’  la forma della linea che risulta un utile principio organizzativo per estrarre delle utili informazioni. Sfortunatamente pero’ i dati non sempre cooperano e si dispongono lungo una retta. Consideriamo, per esempio, l’insieme mostrato di seguito.

E’ facile capire che non c’e’ nessuna linea che possa rappresentare tali dati accuratamente. La ragione e’ che questi dati si dispongono in un insieme di tre cluster molto “stretti”. Anche se puo’ sembrare strano un aspetto fondamentale di qualsiasi forma e’ il numero di pezzi connessi in cui l’insieme puo’ essere diviso (In matematica, uno spazio topologico si dice connesso se non può essere rappresentato come l'unione di due o più insiemi aperti non vuoti e disgiunti. In modo poco formale ma abbastanza intuitivo, possiamo dire che la connessione è la proprietà topologica di un insieme di essere formato da un solo "pezzo"). In questo caso quindi la forma non puo’ essere quella di una linea ma quella di 3 pezzi connessi.

A questo punto potremmo pensare di procedere assumendo che quasiasi insieme di dati possa essere approssimato da una linea, da una famiglia di clusters o una famiglia di linee. Qui di seguito un altro insieme di dati che dimostra come questo non sia vero.  Chiaramente la regressione lineare (cerchio a destra) in un tale contensto e’ inutile e lo possiamo vedere grazie al fatto che ci rendiamo conto che la forma e’ circolare e cioe’ che possiamo vedere come si dispongono i punti.

Un altro esempio in cui la forma rassomiglia a quella di una Y. Questa e’ un’altra forma che spesso capita di incontrare nell’analisi dei big data. Il sistema ha un cuore centrale e 3 filamenti che si estendono a partire da esso. Questo puo’ rappresentare una situazione dove il cuore rappresenta il comportamento tipico e I filamenti invece dei comportamenti estremi dove il sistema sta meno frequentemente. E’ chiaro che questa forma e’ diversa da tutte le altre menzionate.

Esistono purtroppo infinite varieta’ di forme possibili nei dati reali e non solo quelle poche riportate fin qui come mostrato nell’immagine qui sotto.

E le difficolta’ non finiscono qui. Cosa succede se i punti si trovano in uno spazio a piu’ di 3 dimensioni? Come potremmo renderci conto che si tratta di un cerchio o di una linea?

O meglio: come possiamo insegnare ad un computer a trovare per esempio un cerchio?

Queste sono alcune delle questioni che emergono quando si analizzano i big data. Le risposte vengono dai campi piu’ disparati quali: machine learning, data mining, advanced statistic ecc. Ultimamente comunque come gia’ anticipato un valido contributo sembra venire dalla geometria e in particolare dalla topologia. Quest’ultima chiamata anche la “geometria dei fogli di gomma” e’ lo studio delle proprieta’ delle figure e delle forme che non cambiano quando viene effettuata una deformazione senza strappi, sovrapposizioni o incollature. Per un topologo una sfera e un cubo sono la stessa cosa. Operazioni come questa vengono chiamate deformazioni e due oggetti vengono considerati uguali se e’ possibile deformare uno nell’altro. I topologi studiano gli spazi assegnandogli degli oggetti algebrici chiamati invarianti. Nel caso particolare dell’applicazione della topologia all’analisi dei dati (TDA) l’invariante scelto e’ la cosiddetta “persistenza omologa”. L’omologia ordinaria misura il numero di “buchi” in uno spazio che non possono essere riempiti. Pensiamo ad una sfera. Se disegniamo una curva chiusa sulla sua superficie questa racchiudera’ uno disco di 2 dimensioni e potra’ avere il raggio che vogliamo anche tendente a zero. In questo senso significa che non ci sono buchi sulla superficie di una sfera altrimenti non avremmo potuto ridurre il disco fino ad avere dimensione nulla.

Al contrario questo non e’ vero per la superficie della sfera stessa che racchiude un “vuoto” tridimensionale che non puo’ essere riempito. I numeri di Betti contano quanti buchi non riempibili sono presenti per uno spazio di ogni dimensione.

· β0(X) e’ il numero di componenti connesse (o 0-cicli), in pratica il numero di pezzi separati di cui e’ composto lo spazio

· β1(X) conta i buchi fatti “a circonferenza” dello spazio (1-cicli come quelli di una ciambella)

· β2(X ) conta i vuoti bidimensionali dello spazio (2-cicli come quelli della sfera, del pallone o di una camera d’aria etc).

Qui di seguito il primo numero di Betti per le consonanti coreane.

Consideriamo adesso un caso bidimensionale con i dati rappresentati da un insieme discreto di punti come mostrato.

L’idea e’ quella di far crescere intorno ad ogni punto un disco di diametro d. Se d inizialmente e’ molto piccolo allora nessuno dei dischi s’interseca. Ma una volta che d cresce (vedi sotto) allora i dischi  iniziano a toccarsi dando origine a dei numeri di Betti diversi da zero. Osserviamo che a partire da d=d1 e fino a che d=d2, avremo un buco tra i 4 dischi cioe’ il buco persistera’ mentre d va da d1 fino a d2. Questo lo possiamo rappresentare con un grafico che prende il nome di barcode come mostrato sotto.

Ritorniamo adesso al caso discreto di punti introdotto prima e iniziamo a far crescere i dischi. Fermandoci ad un diametro leggermente superiore a d=1 avremo la seguente situazione. Ci sono due buchi uno in alto a sinistra all’interno del pentagono e uno in basso a destra all’interno del quadrato.

Quando il diametro d supera ~1.5 si forma un unico buco grande come mostrato sotto.

L’omologia persistente monitora i numeri di Betti utilizzando i barcode al variare del diametro d. Le barre lunghe indicano delle caratteristiche (features) dei dati che possono essere significative. Le barre corte invece spesso nascono dal rumore e possono essere scartate. Quello che si fa quindi e’ passare da una collezione discreta di punti ad una sequenza piu’ complicata di spazi che modellano meglio i dati di quanto possa fare una semplice correlazione lineare.

Gunnar Carlsson della Stanford University e’ uno dei pionieri della TDA. Insieme a dei colleghi ha fondato la compagnia AYASDI, sviluppando un software che si e’ dimostrato un valido strumento nell’analisi dei dati di banche, finanza, governo e industrie. Qui di seguito qualche esempio di applicazione. Dall’analisi di un database di una banca contenente circa 6 milioni di transazioni con circa 300 attributi il software e’ stato capace di isolare quelle fraudolente indicate in rosso.

Un altro esempio e’ dato dall’applicazione del software al mondo delle fabbriche di semiconduttori. Sono state analizzate piu’ di 1000 linee di produzione con circa 500 attributi per ogni linea identificando quelle con problemi di bassa qualita’ dei loro prodotti come mostrato nell’mmagine sottostante.

In definitiva cosa rende cosi’ potente l’applicazione della topologia nell’analisi dei dati rispetto alle tecniche piu’ tradizionali? La risposta e’ nelle seguenti 3 proprieta’ della topologia.

1. Indipendenza dal sistema di coordinate: la topologia studia le proprieta’ geometriche degli oggetti che non dipendono dal particolare sistema di riferimento utilizzato per rappresentarli

2. Invarianza rispetto alle deformazioni: la topologia studia le proprieta’ delle curve e superfici che non cambiano quando vengono stirate.

3. Rappresentazione compressa: la topologia costruisce delle rappresentazioni combinatorie di oggetti continui. Un cerchio (curva continua) puo’ essere rappresentato da una rete esagonale costituita cioe’ da 6 nodi e 6 spigoli (edges).